精英反向学习带扰动因子的混沌蚁狮算法
文章目录
摘要:针对蚁狮算法易陷入局部最优、收敛速度慢的缺点,本文提出了基于精英反向学习带扰动因子的混沌蚁狮算法。该算法首先通过对蚂蚁的随机游走公式引入扰动因子,有效提高了寻优精度,避免算法陷入局部最优,有效平衡了全局最优搜索与局部最优搜索;对蚁狮的精英个体进行反向学习生成精英反向解,增加了种群多样性;通过比较当前最优解与精英反向解,选出优异个体作为新的全局最优解;最后在蚂蚁受轮盘赌选择蚁狮、精英蚁狮影响的随机游走公式中引入Logistic混沌映射,有效提高了算法的全局搜索能力和寻优精度。
1.蚁狮优化算法
基础蚁狮优化算法的具体原理参考,我的博客:https://blog.csdn.net/u011835903/article/details/107726004
2. 改进蚁狮优化算法
2.1 加入扰动因子 q 的蚂蚁随机游走公式
在蚂蚁随机游走公式中添加扰动因子, 增大了 蚂蚁随机游走初期的游走范围, 加强全局勘探能力, 增加了搜索到全局最优值的概率。在算法后期勘探 范围由大到小过渡, 增强局部搜索能力, 扰动因子
q
q
q 使得算法在全局搜索和局部搜索中有了一个较好的 平衡, 并且有效的避免了陷入局部最优的问题, 从而 得到最优解。扰动因子
q
q
q 定义如下:
q
=
[
(
−
α
×
t
T
)
5
+
1
]
×
β
.
(11)
q=\left[\left(-\alpha \times \frac{t}{T}\right)^{5}+1\right] \times \beta .\tag{11}
q=[(−α×Tt)5+1]×β.(11)
其中,
t
t
t 是当前迭代次数;
T
T
T 为最大迭代次数。 通过大量实验证明,
α
=
10
,
β
=
0.15
\alpha=10, \beta=0.15
α=10,β=0.15 时寻优效果最 好, 改进后的蚂蚁随机游走公式为:
X
i
t
=
[
(
X
i
t
−
a
i
)
×
(
b
i
−
c
i
t
)
d
i
t
−
a
i
+
c
i
]
×
q
.
(12)
X_{i}^{t}=\left[\frac{\left(X_{\mathrm{i}}^{t}-a_{i}\right) \times\left(b_{i}-c_{i}^{t}\right)}{d_{i}^{t}-a_{i}}+c_{i}\right] \times q .\tag{12}
Xit=[dit−ai(Xit−ai)×(bi−cit)+ci]×q.(12)
2.2 Logistic 混沌映射
由于蚁狮种群的适应度在算法迭代过程中仍然存在着相对较差的个体,而通过轮盘赌可能会选择到适应度较差的蚁狮。若蚂蚁围绕该蚁狮进行游走会影响算法整体的寻优效率,将 Logistic 混沌映射与蚂蚁受轮盘赌选择蚁狮与精英蚁狮影响的随机游走公式相结合,使蚂蚁能够进行混沌搜索,提高蚂蚁的寻优效率,增大算法跳出局部最优解的能力。
Logistic 混池映射如下:
x
n
∈
rand
(
1
)
,
x
n
+
1
=
4
×
x
n
(
1
−
x
n
)
.
\begin{gathered} x_{n} \in \operatorname{rand}(1), \\ x_{n+1}=4 \times x_{n}\left(1-x_{n}\right) . \end{gathered}
xn∈rand(1),xn+1=4×xn(1−xn).
其 中,
x
n
x_{n}
xn 是 0 到 1 中的一个随机数, 在公式 (10)中加入混池因子, 有效提高了算法的寻优效 率, 并将本次计算的蚂蚁位置作为下一代的初始位 置, 改进后的公式为:
A
n
t
i
t
=
(
R
A
t
+
R
E
t
2
)
×
x
n
+
1
.
(15)
A n t_{i}^{t}=\left(\frac{R_{A}^{t}+R_{E}^{t}}{2}\right) \times x_{n+1} .\tag{15}
Antit=(2RAt+REt)×xn+1.(15)
2.3 精英反向学习
反向学习(opposition - based learning, OBL) 由 Tizhoosh
[
15
]
^{[15]}
[15] 斱授千 2005 年提出, 主要是求问题可行 解的反向解, 并对当前可行解与反向解进行评估, 从 中选择较优的解作为下一代个体。反向学习能有效 提高群体多样性, 从中选择较好的解作为当前最优 解,大大提高了算法的效率。本文合理利用精英蚑 狮个体的有效信息, 通过对精英个体的反向学习产 生精英反向解, 增加了种群多样性, 加快了算法的收 敛連度。
定义 1 反向数 Opposition Number
[
16
]
{ }^{[16]}
[16] : 若
x
∈
x \in
x∈
[
a
,
b
]
[a, b]
[a,b] 且
x
∈
R
x \in R
x∈R, 则其反向数
x
∗
x^{*}
x∗ 为:
x
∗
=
a
+
b
−
x
.
x^{*}=a+b-x \text {. }
x∗=a+b−x.
定义 2 反向点 Opposition Point
[
16
]
{ }^{[16]}
[16] : 若
p
=
p=
p=
(
x
1
,
x
2
,
…
,
x
N
)
\left(x_{1}, x_{2}, \ldots, x_{N}\right)
(x1,x2,…,xN) 之间的任意
N
\mathrm{N}
N 维空间中的点为
x
∈
x \in
x∈
[
x
i
min
,
x
i
max
]
、
x
i
∈
[
a
i
,
b
i
]
\left[x_{i \min }, x_{i \text { max }}\right] 、 x_{i} \in\left[a_{i}, b_{i}\right]
[ximin,xi max ]、xi∈[ai,bi], 则它反向学习的解如下 所示
[
17
]
{ }^{[17]}
[17] :
{
P
∗
=
(
x
1
∗
,
x
2
∗
,
…
,
x
D
∗
)
x
i
∗
=
x
i
min
+
x
i
max
−
x
i
.
\left\{\begin{array}{l} P^{*}=\left(x_{1}^{*}, x_{2}^{*}, \ldots, x_{D}^{*}\right) \\ x_{i}^{*}=x_{i \text { min }}+x_{i \max }-x_{i} . \end{array}\right.
{P∗=(x1∗,x2∗,…,xD∗)xi∗=xi min +ximax−xi.
定义 3 精英反向学习(elite opposition-based learning, EOBL)
[
17
]
{ }^{[17]}
[17] 。
本文中将蚂蚁与蚁狮种群的整体适应度中的精 英个体赋值给精英蚁狮, 定义为
D
F
i
=
D F_{i}=
DFi=
(
D
F
1
,
D
F
2
,
…
,
D
F
τ
)
\left(D F_{1}, D F_{2}, \ldots, D F_{\tau}\right)
(DF1,DF2,…,DFτ) 。其 中
D
F
i
∈
[
a
i
,
b
i
]
D F_{i} \in\left[a_{i}, b_{i}\right]
DFi∈[ai,bi],
[
a
i
,
b
i
]
\left[a_{i}, b_{i}\right]
[ai,bi] 为蚂虽与蚁狮按适应度排序后的最小最大 值。则对应的精英反向解
D
F
i
∗
=
(
D
F
1
∗
,
D
F
2
∗
,
…
D F_{i}^{*}=\left(D F_{1}^{*}, D F_{2}^{*}, \ldots\right.
DFi∗=(DF1∗,DF2∗,…,
D
F
T
∗
D F_{T}^{*}
DFT∗ ) 定义为:
D
F
i
∗
=
a
i
+
b
i
−
D
F
i
.
D F_{i}^{*}=a_{i}+b_{i}-D F_{i} .
DFi∗=ai+bi−DFi.
将式 (9) 中最优的适应度与精英蚁狮、精英反 向解作比较, 选出适应度最好的作为当前最优值。

3.实验结果
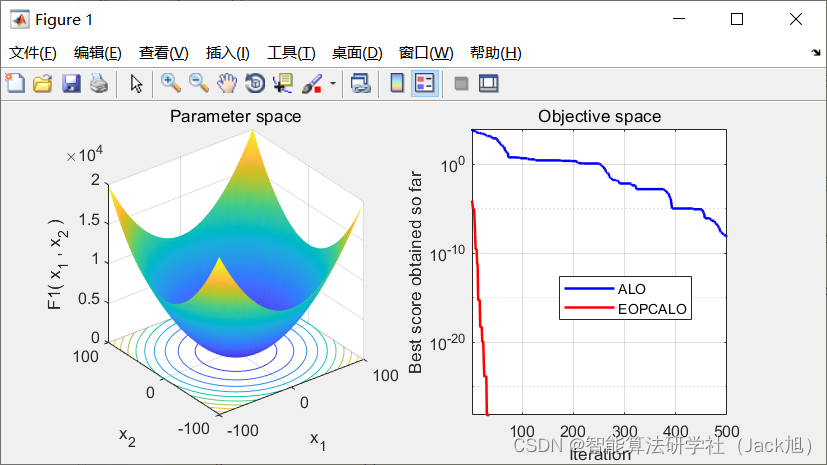
4.参考文献
[1]王茜,何庆,林杰,杨荣莹.精英反向学习带扰动因子的混沌蚁狮算法[J].智能计算机与应用,2020,10(08):51-57.


























 175
175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










