计算空间内三个基站定位坐标

如果O、A、B基站三个基站处在空间的高处，距离地面3米，基站的测距差距在10cm，标签在地面。

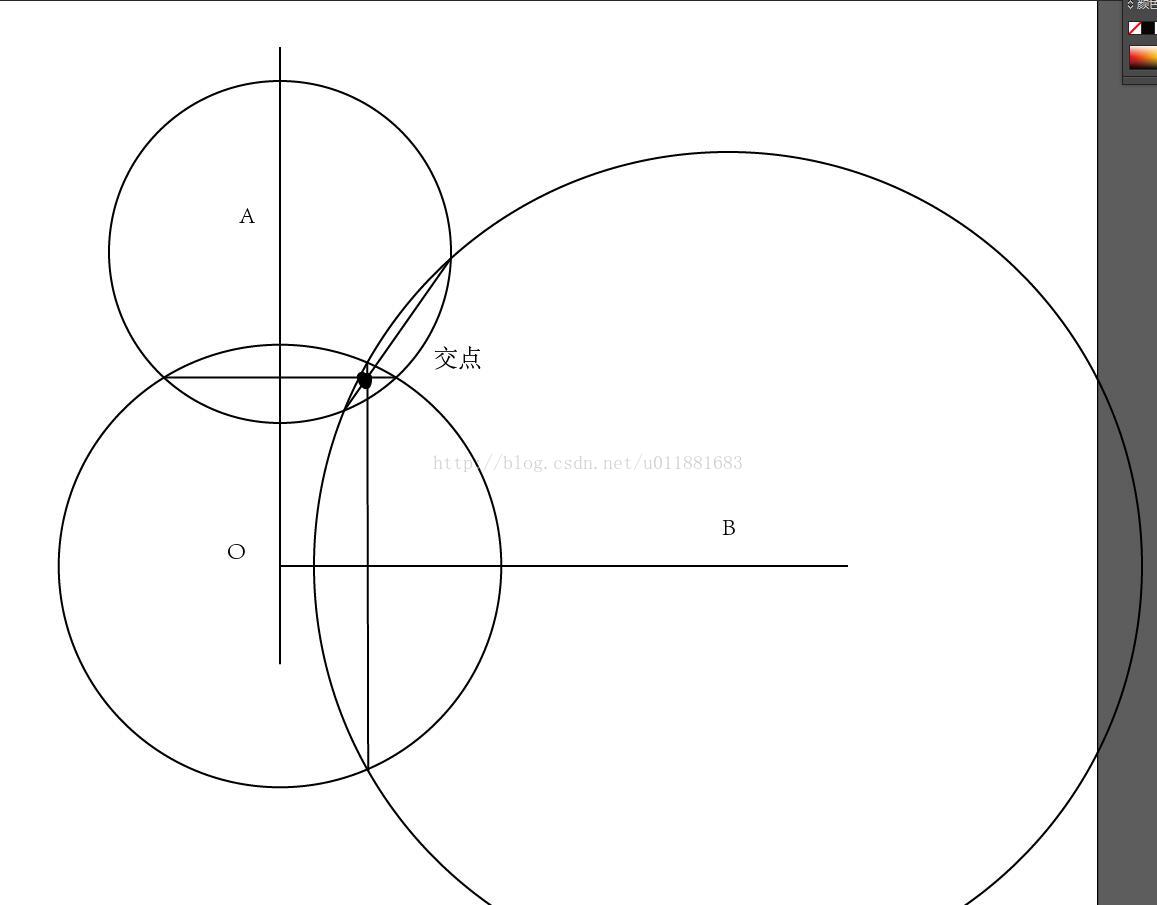
那么，如果计算到平面上则可以肯定3个圆是相交的状态。而且交点一定是在两个圆交点的连线上称之为【根轴】。

如果是这样就可以计算每每两个圆的根轴可以得到三个根轴。

每每三个根轴交叉可以得到三个交点。

再求得三个交点的中心即为当前的坐标。

点击打开链接转载自两个圆的交点

/// <summary>
        /// 计算两个圆的交点坐标
        /// </summary>
        /// <param name="A"></param>
        /// <param name="B"></param>
        /// <returns></returns>
        public Point[] CircleInsect(Circle A, Circle B)
        {

            Point[] points = new Point[2] { new Point(), new Point() };

            double x1 = A.Center.X;
            double y1 = A.Center.Y;
            double r1 = A.Radius;
            double x2 = B.Center.X;
            double y2 = B.Center.Y;
            double r2 = B.Radius;
            double Dis = Math.Sqrt((A.Center.X - B.Center.X) * (A.Center.X - B.Center.X) +
                (A.Center.Y - B.Center.Y) * (A.Center.Y - B.Center.Y)); // 圆心距离
            if (double.Equals(x1, x2) && double.Equals(y1, y2) && (double.Equals(r1, r2))) // 两圆重合
            {
                Console.WriteLine("The two circles are the same");
            }
            if ((Dis > r1 + r2) || Dis < Math.Abs(r1 - r2))     // 两圆相离或者内含
            {
                Console.WriteLine("The two circles have no intersection");
            }
            if (double.Equals(Dis, r1 + r2) || double.Equals(Dis, Math.Abs(r1 - r2))) // 两圆有一个交点(即两圆相切[内切和外切])
            {
                if (double.Equals(Dis, r1 + r2))// 外切
                {

                    if (double.Equals(x1, x2) && !double.Equals(y1, y2))
                    {
                        if (y1 > y2)
                        {
                            points[0].X = x1 = x2;
                            points[0].Y = y1 - r1;
                        }
                        else
                        {
                            points[0].X = x1 = x2;
                            points[0].Y = y1 + r1;
                        }
                    }
                    else if (!double.Equals(x1, x2) && double.Equals(y1, y2))
                    {
                        if (x1 > x2)
                        {
                            points[0].X = x1 - r1;
                            points[0].Y = y1 = y2;
                        }
                        else
                        {
                            points[0].X = x1 + r1;
                            points[0].Y = y1 = y2;
                        }
                    }
                    else if (!double.Equals(x1, x2) && !double.Equals(y1, y2))
                    {
                        // 外切情况，两圆的交点在圆心AB连线上
                        double k1 = (y2 - y1) / (x2 - x1);
                        double k2 = -1 / k1;
                        points[0].X = x1 + (x2 - x1) * r1 / Dis;
                        //points[0].Y=y1+k2*(points[0].X-x1);
                        points[0].Y = y1 + (y2 - y1) * r1 / Dis;
                    }
                }
                else if (double.Equals(Dis, Math.Abs(r1 - r2))) // 内切 (是否要考虑A包含B 还是B包含A，对结果是否有影响)
                {
                    if (double.Equals(x1, x2) && !double.Equals(y1, y2))
                    {
                        if (r1 > r2) // A内含B
                        {
                            if (y1 > y2)
                            {
                                points[0].X = x1 = x2;
                                points[0].Y = y1 - r1;
                            }
                            else
                            {
                                points[0].X = x1 = x2;
                                points[0].Y = y1 + r1;
                            }
                        }
                        else // B 内含A
                        {
                            if (y1 > y2)
                            {
                                points[0].X = x1 = x2;
                                points[0].Y = y1 + r1;
                            }
                            else
                            {
                                points[0].X = x1 = x2;
                                points[0].Y = y1 - r1;
                            }
                        }
                    }
                    else if (!double.Equals(x1, x2) && double.Equals(y1, y2))
                    {
                        if (r1 > r2)
                        {
                            if (x1 > x2)
                            {
                                points[0].X = x1 - r1;
                                points[0].Y = y1 = y2;
                            }
                            else
                            {
                                points[0].X = x1 + r1;
                                points[0].Y = y1 = y2;
                            }
                        }
                        else
                        {
                            if (x1 > x2)
                            {
                                points[0].X = x1 + r1;
                                points[0].Y = y1 = y2;
                            }
                            else
                            {
                                points[0].X = x1 - r1;
                                points[0].Y = y1 = y2;
                            }
                        }
                    }
                    else if (!double.Equals(x1, x2) && !double.Equals(y1, y2)) // 是否要考虑内含关系(求坐标时是否有影响)
                    {
                        // 内切情况，交点在AB连线的延长线上，要考虑切点的位置 
                        double k1 = (y2 - y1) / (x2 - x1);
                        double k2 = -1 / k1;
                        points[0].X = x1 + (x1 - x2) * r1 / Dis;
                        //points[0].Y = y1 + k2 * (points[0].X - x1);
                        points[0].Y = y1 + (y1 - y2) * r1 / Dis;
                    }
                }
            }
            if ((Dis < r1 + r2) && Dis > Math.Abs(r1 - r2))    // 两圆有两个交点(内交或者外交) 【内交与外交的情况是否一样？】
            {

                if (double.Equals(x1, x2) && !double.Equals(y1, y2))  // 圆A和圆B 横坐标相等
                {
                    double x0 = x1 = x2;
                    double y0 = y1 + (y2 - y1) * (r1 * r1 - r2 * r2 + Dis * Dis) / (2 * Dis * Dis);
                    double Dis1 = Math.Sqrt(r1 * r1 - (x0 - x1) * (x0 - x1) - (y0 - y1) * (y0 - y1));
                    points[0].X = x0 - Dis1;
                    points[0].Y = y0;
                    points[1].X = x0 + Dis1;
                    points[1].Y = y0;
                }
                else if (!double.Equals(x1, x2) && double.Equals(y1, y2)) // 圆A和圆B 纵坐标相等
                {
                    double y0 = y1 = y2;
                    double x0 = x1 + (x2 - x1) * (r1 * r1 - r2 * r2 + Dis * Dis) / (2 * Dis * Dis);
                    double Dis1 = Math.Sqrt(r1 * r1 - (x0 - x1) * (x0 - x1) - (y0 - y1) * (y0 - y1));
                    points[0].X = x0;
                    points[0].Y = y0 - Dis1;
                    points[1].X = x0;
                    points[1].Y = y0 + Dis1;
                }
                else if (!double.Equals(x1, x2) && !double.Equals(y1, y2)) // 横纵坐标都不等 
                {
                    double k1 = (y2 - y1) / (x2 - x1);//AB的斜率
                    double k2 = -1 / k1;             // CD的斜率
                    double x0 = x1 + (x2 - x1) * (r1 * r1 - r2 * r2 + Dis * Dis) / (2 * Dis * Dis);
                    double y0 = y1 + k1 * (x0 - x1);
                    double Dis1 = r1 * r1 - (x0 - x1) * (x0 - x1) - (y0 - y1) * (y0 - y1); //CE的平方
                    double Dis2 = Math.Sqrt(Dis1 / (1 + k2 * k2));//EF的长，过C作过E点水平直线的垂线，交于F点
                    points[0].X = x0 - Dis2;
                    points[0].Y = y0 + k2 * (points[0].X - x0);
                    points[1].X = x0 + Dis2;
                    points[1].Y = y0 + k2 * (points[1].X - x0);
                }
            }
            return points;
        }

/// <summary>
        /// 判断1,2直线和3,4直线的交点
        /// </summary>
        /// <param name="point1"></param>
        /// <param name="point2"></param>
        /// <param name="point3"></param>
        /// <param name="point4"></param>
        /// <returns></returns>
        public Point GetCrossPoint(Point point1, Point point2, Point point3, Point point4)
        {
            double pD_x = point1.X;
            double pD_y = point1.Y;
            double pB_x = point2.X;
            double pB_y = point2.Y;

            double pC_x = point3.X;
            double pC_y = point3.Y;
            double pA_x = point4.X;
            double pA_y = point4.Y;

            double k_y = (pB_x * pC_y * pD_y - pD_x * pB_y * pC_y - pA_y * pB_x * pD_y + pD_x * pB_y * pA_y + pC_x * pA_y * pD_y - pA_x * pC_y * pD_y - pC_x * pB_y * pA_y + pA_x * pB_y * pC_y) /
                (pD_y * pC_x - pA_x * pD_y - pB_y * pC_x + pA_x * pB_y + pB_x * pC_y - pD_x * pC_y - pA_y * pB_x + pA_y * pD_x);

            double k_x = (pD_y * (pC_x - pA_x) * (pB_x - pD_x) - pA_y * (pC_x - pA_x) * (pB_x - pD_x) + pA_x * (pC_y - pA_y) * (pB_x - pD_x) + pD_x * (pD_y - pB_y) * (pC_x - pA_x)) /
                ((pC_y - pA_y) * (pB_x - pD_x) + (pD_y - pB_y) * (pC_x - pA_x));

            return new Point(k_x, k_y);
        }

/// <summary>
        /// 计算两基站相对于人的中心点
        /// </summary>
        /// <returns></returns>
        private Point PersonPosition(double lenAOne, double lenATwo, double lenAThree)
        {
            //计算两个圆的交点组
            Point[] points1 = CircleInsect(new Circle(_ANCHOR0, lenAOne), new Circle(_ANCHOR1, lenATwo));

            Point[] points2 = CircleInsect(new Circle(_ANCHOR0, lenAOne), new Circle(_ANCHOR2, lenAThree));

            Point[] points3 = CircleInsect(new Circle(_ANCHOR2, lenAThree), new Circle(_ANCHOR1, lenATwo));

            if (points1[0].X == 0.0 && points1[0].Y == 0.0)
            {
                //返回中心坐标
                return centerPoint;
            }
            if (points2[0].X == 0.0 && points2[0].Y == 0.0)
            {
                //返回中心坐标
                return centerPoint;
            }
            if (points3[0].X == 0.0 && points3[0].Y == 0.0)
            {
                //返回中心坐标
                return centerPoint;
            }

            //计算每每两条直线的交点
            Point point1 = GetCrossPoint(points1[0], points1[1], points2[0], points2[1]);

            Point point2 = GetCrossPoint(points1[0], points1[1], points3[0], points3[1]);

            Point point3 = GetCrossPoint(points3[0], points3[1], points2[0], points2[1]);

            centerPoint = new Point((point1.X + point2.X + point3.X) / 3,
               (point1.Y + point2.Y + point3.Y) / 3);

            //返回中心坐标
            return centerPoint;
        }