原文出处:Knowledge-based Graph Document Modeling
注:译者英文水平有限,翻译的不是很好,希望大家海涵
对于原文,我只翻译到算法实现结束,后面的相关内容如大家有兴趣,可以自己去看一看
摘要
我们提出了一个基于图的语义模型,用来表示文档的内容。我们的方法依赖于对语义网的应用(译者认为其实是依赖于对语义网范例的应用),它就是DBpedia知识库,利用DBpedia可以获得关于实体以及它们之间关于语义关系的非常细化的信息,从而引出了一个知识丰富的文档模型。我们通过两个任务来论证这些语义表征:实体排名和计算文档语义相似度。为了达到这个目的,我们将DBpedia的结构和一种对概念关联的信息论度量方法结合起来,基于它(DBpedia structure)的显著语义关系,还有通过图编辑距离的度量方法来计算语义相似度,最后再加上我们利用匈牙利算法从而可以找到文档实体间的最佳匹配。实验的结果展示出我们的一般模型优于建立在传统方法上的基准,并且实现了非常高效的性能,和那些已经被用于来协调解决这些特殊任务的高度专业化方法的性能相比,也是非常接近的。
分类与主题描述:信息存储与检索,人工智能:语义网,自然语言处理
关键词:文档建模,语义网挖掘,DBpedia,实体联系,文档语义相似度
近些年,我们可以看到业界出现了对语义技术和嵌入在大范围应用里的语义模型方法的大规模的工作或研究,主要包括诸如终端用户应用之类的,比如,在线问答,文档搜索和网页搜索结果聚类。对于这样的趋势,更有甚者,很多研究的努力的集中在对大规模机器可读性知识的自动攫取,它是通过挖掘大量的像网页这样的文本数据知识库以及协作构建资源来实现的。这样便导致了近年来出现了很多卓越的,新生的并且不尽相同的自然语言处理以及信息检索方法。
尽管最近的这些研究趋势表明语义信息和知识丰富型方法可以被有效的用于高端的信息检索和自然语言处理难题,但是百业待举,在这个领域,为了更有效的开发这些丰富的模型和改进现有的工艺水平,仍有很多事要做。大部分的方法依靠于文档的表示,实际上,也就是单一的依靠形态句法信息,比如向量空间模型。尽管越来越多的成熟模型已经被提出,包括概念级和建立向量空间,这些仍然没有从诸如YAGO和DBpedia这样的大规模覆盖的知识库里挖掘出关系型知识和网络结构。
在这篇文章里,我们致力于通过知识丰富型方法来表示关联数据网,从而攻克这些问题。我们方法的关键点是将细化的关系词汇与概念关联的信息论度量方法结合,再借助于大量的结构化知识,比如编码在DBpedia内的消歧实体和显著语义关系,来构造出一个基于图的文本翻译器。
我们的贡献主要如下:
(1)我们提出了一种基于图的文档模型,并且给出了一种方法来构造出结合了消歧实体和细化的语义关系的文本的结构化表示。
(2)我们提出来大量的信息论度量在本体上来给不同的语义关系赋权值,并且依据它们连接的概念自动的量化它们的相关度。在语义图中边就是这样赋值的,从而可以捕捉到概念之间的关联程度,同样也可以找出它们不同的特殊性级别。
(3)我们的对模型的评估通过两种高度相关的任务,即实体排名和计算文档相似度。我们展示出的方法不仅优于标准的传统方法,比如'flat',文档表示,而且得出了和那些准们致力于这方面难题的高度专业化方法相似的结果。
(4)为了应用我们的语义图计算文档相似度,基于图的编辑距离技术,我们开发了一种新的方法。我们的方法将在本体内计算语义距离视为一种概念匹配问题,并且使用了匈牙利算法来解决这种组合优化问题。
综上所述,我们可以提供一套完整的框架,基于这个框架,将文档连接到一个可引用的知识库,从而将文档语义化,并且知识资源的子图被用于复杂语言理解任务,比如实体排名和文档语义相似度。实体排名的结果体现出当我们和简单的无权值路径相比,我们的加权方式有利于我们更好的估计实体的相关度。而且,通过对结构化的文本表示补充大量的知识,我们能够实现在计算文档语义相似度时拥有健壮性能的目标。这样,不仅完成了不论是基于词还是概念向量空间的‘flat'方法,同事也提供了一个一般的,实际上又无参数的模型。
我们的方法通过将DBpedia作为后端本体来产生文本内容的结构化表示。为了达到这个目的,我们选择基于图的方法,如果:
(i)它们本质上市通用的,并且可以被用于任何的知识图,比如一个知识资源可以被视作一个图,而不论它里面特殊性的词汇。
(ii)它们已经被有效的公布出用于语言理解任务。
在下文,章节2.1中我们首先简单的介绍DBpedia,也就是应用于我们方法的资源,章节2.2和2.3将详细描述我们的主要方法。
2.1 DBpedia
我们的方法依赖于一个潜在的知识库中被编码的信息和结构。在此工作期间,我们选择DBpedia,因为它提供了一个广范围覆盖的知识库,并且拥有很多细化的实体间显式语义关系。不仅如此,我们的方法还适用于其他的词汇或本体资源,比如YAGO,可被转换成一个含有消歧实体和显式语义关系的知识图。
DBpedia是一个语义网的应用范例,它从Wikipedia中攫取结构化的信息并且将这些信息在网上变为可用的完整的一个本体。为了能够自动的获得大量实体的属性和关系,DBpedia背后的关键点在于解析信息框,也就是从Wikipedia页面中得出属性总结表。这些更进一步的被内嵌在基于语义网形式主义的一个本体中,比如:(i)在关联数据的最佳实践上表示数据;(ii)利用RDF对语义关系编码,RDF是一个一般的基于图的数据模型,一般用来描述宾语和它们之间的关系。在下文中,我们将提到RDF三元组在DBpedia上组成了主语,谓语和宾语,并且关系是有向的从主语Subj指向宾语Obj,这个关系即是谓语Pred。
很自然的,我们将DBpedia视作一个图,它的节点就是实体,边则可以捕捉它们之间的显式语义关系。举个例子:一个实体“Bob Dylan”在DBpedia里是被连接至其他实体的,它是通过这样的方式:db:Bob_Dylan rdf:type dbo:MusicalArtist or db:Bob_Dylan dbo:genre db:Folk_rock, 等等。如今我们将演示如何利用这样的结构,从包括实体的集合中,比如那些在自然语言文本中所提到的,来构造基于图的表示。
2.2 语义图的构造
令Cdb为DBpedia的概念和实体全集,C为它任意的子集,以输入形式给出,比如文档中提到的实体集合。我们方法的第一阶段是,我们通过输入的实体集合建一个加标签的有向图G=(V,E),包含:(i)实体本身,(ii)它们之间的语义关系,(iii)任何在本体中与输入中任意实体相关的附加实体。即就是,在DBpedia中,C包含于V包含于Cdb,并且E包含于V x R x V,r∈R。例如:rdf:type, dbo:birthDate or dbp:genre (我们并不区分断言推理和术语推理,因为用我们潜在的资源,词汇的特殊性级别仍然对我们是不可知的)。还有,我们想给每一条边赋予权值w,(vi,r,vj)∈E,为了捕捉源节点和目标节点间的相关程度,比如说就是两个实体间有多强的相连关系。
为了构造我们的语义图,我们开始输入一系列的实体C并且建立加标签的有向图G=(V,E),如下:(a)首先,我们定义所有输入的concept组成G的节点集合V,也就是我们令V:=C;(b)接着,我们通过DBpedia上它们之间的路径来连接它们。V里的节点通过在DBpedia图中深度优先搜索扩展成一张图并不断地增加所有的出边关系r,从而增加所有的长度小于等于L的简单有向路径v,v1,...,vk,v',比如:V:=V∪{v1,...,vk},E:=E∪{(v,r1,v1),...,(vk,rk,v')}。从而,我们获得了DBpedia上包含了初始concepts的一个子图,与所有的边和中间概念一起,被沿着总长度小于等于L的所有连接它们的路径所发现。在此工作期间,根据我们之前的相关工作所得出的大量证明,我们设定L=2。
图1描述了一个从实体集 {db:Bob_Dylan, db:Monterey_Country_Fairgrounds, db:Mozambique_(Song), db:Johnny_Cash}} 产生语义图的例子:
例如:从这个句子中“Dylan played Mozambique at Monterey right before Cash”发现相关的实体。从这些种子实体开始,我们运用深度优先搜索来增加相关的中间概念与关系,来构成G(例如,foaf:Person or db:Folk_music)。这样,我们可以得到一个富有语义的图:额外的节点和边提供给我们一个非常结构化的上下文,使得这些初始概念被大量的实体和显式语义关系所连接。
2.3 语义关系加权
到目前为止,我们的方法简单的将一系列输入的实体集转化成了DBpedia的图---比如,本质上等同于用基于图的方法来进行词义消歧。然而,与像WordNet这样的词汇资源所不同的是,我们的后端本体包含很多不同的,细化的语义关系:因此,在建立图时,并不是所有的关系都是拥有同样的信息,并且问题的提出包含了关于什么样的信息将被考虑。比如,在我们的例子中,由于DBpedia图的高密度,db:Bob_Dylan和db:Johnny_Cash之间存在着多条路径。连通的路径,包含了 高信息量的关系(比如,两个实体通过dbo:associatedBand有向连接起来),同样地,它们也都属于实体rdf:type foaf:Person,这个实体则指向了大量的实体(比如DBpedia里所有的人)并且拥有很低的区别力,因为它太一般了,例如,为了确定对于计算语义相似度时关系的重要性,Person这个关系就显得很不重要。然而之前的工作我们限制了语义关系,将语义图建立成了一个小的,人工选择的集合,我们在这里做出选择而不是采用基于关系特殊性的边加权的自动方法。这是因为,人工的方法可以保证全局的质量,它并不需要衡量并且需要被每个知识层轮流的调整。因此,我们通过给边加权来扩展我们的语义图。权值则意味着用来捕捉图中概念之间的相关程度(也就是语义关系)。主要的点就是:对于一个给定的源节点,那些边和目标节点对于它来说要是最具有特殊性的。我们给边赋值的核心在于信息量IC:
这里P(Wpred)是自由变量Xpred描述边类型的概率,通俗的将就是某边在边全集里占的比例。这个方法假定了特殊性是对相关性的一个比较好的代理。我们可以计算所有的谓语的IC值,因为我们有DBpedia的完整图,并且可以查询所有潜在的随机变量Xpred。在我们的例子中,一条边被打标签rdf:type 将相应的得到一个IC值,但会小于被打标签dbo:associatedBand的边的IC值。
联合信息量(jointIC)
虽然我们语义关系的信息量提供给我们一个区别“一般性vs特殊性“的方法,但它只包含了边的先验特殊性,也就是说,不管实体实际上的连接。然而,就像图1中显示的,同一类型的边,比如rdf:type,可以导致非常一般的概念拥有低的区别度(比如foaf:Person),但是对于信息量非常大的概念,比如dbo:MusicalAritist,事实上提供了非常有价值的信息。我们通过添加条件信息量IC(Wobj | Wpred)到我们的加权方式中来捕捉这些有价值的信息,这样解释了概念及谓语指向,从而该边已经被观察。正式地,给定边e=(Subj,Pred,Obj)我们计算联合概率分布的信息量IC(Wpred,Wobj),我们可以采用下面的方程式:
在我们的例子里,rdf:type这条边比dbo:MusicalArtist更高一层,相应地它接收一个更高的权值。(权值越高,则越难出现在meaningful path中,因为在图中求最短路,译者注)
结合信息量(combIC)
对于联合信息量,虽然同时考虑了谓语和宾语的特殊性,然而,对于非频繁出现的宾语和谓语,当两者形成条件概率时,却是不利的,例如,db:American_folk_music从全局来看出现很不频繁,但是却得到了一个高度概率(也就是低的IC)当它遇到了条件dbo:genre。我们建议通过计算联合信息量时假定谓语和宾语相互独立,从而缓解这样的问题。于是我们可以得到下面的方程式:
信息量和逐点相互信息量(IC+PMI)
一个可选择的计算谓语和宾语之间联系程度的方法是通过逐点相互信息量(PMI):
PMI度量两个相互独立的变量结果Wpred和Wobj,而且可以被视为一种方法来度量两个结果的独立性有多少偏差,也就是说,特殊的谓语和宾语将被将被DBpedia图的边所发现。我们在这里的直觉是,使用PMI在jointIC和combIC之间来寻找一个中间立场。我们还结合了PMI与谓语的IC,为了减少我们的偏差,得到更多的信息量,我们有如下方程式:
3. 基于图的实体排名
为了从DBpedia建立有权的语义图,我们提出一种对我们已开发的不同加权方式的外在评估。这是因为语义关系赋值有助于其本身,而且它可以被用于各种不同的任务难题,而不仅仅是语义图构造。比如,RDF三元组排名。因此,我们针对实体排名在知识库上,探索了一个基于任务的评估方法。
任务描述:
实体排名,它的主要任务是对一个给定的实体集合,根据它们与特殊实体的相关性来进行实体排序。在我们的工作中,我们将DBpedia作为我们的知识库, 我们取一个实体,比如:db:Bob_Dylan作为参照,并试图计算db:Johnny_Cash与它到底有多强的相关度,再比如对比db:Folk_music or db:Mozambique_(Song),等等。这个排名任务的优点在于它对我们不同的加权方法提供一个聚焦的,外在的评估方式,而且,还存在已建立的金标准数据集来对比我们的方法。实体排名可以被视作在本质上相似与计算词相关,所不同的是在我们的设置中,我们规定了输入明确的实体参照,而不是潜在的模糊词汇。还有,实体排名同时也在实体链接领域扮演着重要的角色,因为实体链接依赖于估计文本中不同短语的候选实体参照间不同的相关程度。也就是说,在一个全局文档级的实体链接方法中,短语可以通过最大化它们获得的语义重叠度,被连带地明确化,例如,通过知识库里的信息存储。
实体排名方法:
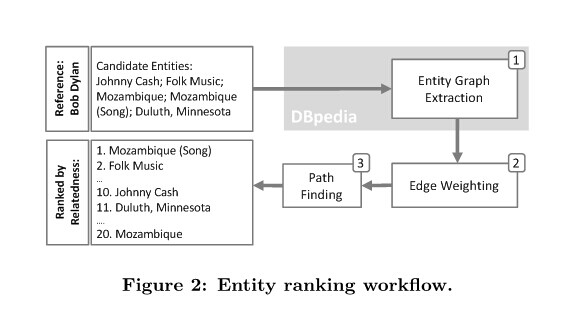
这里,对图2中我们所提出的方法作出概述。给出一个参照实体ref和一个实体集合Ecand(也存在于DBpedia),我们的方法对这些实体排名主要通过以下三个步骤:
(1)我们根据2.2所讲的方法建立一个语义图,使用所有的候选实体Ecand,同时也是作为输入概念的参照实例;
(2)我们用边损耗来给图中的边赋值,这样定义:c(e)=w_max-w(e),w(.)是之前2.3节定义的三个权值方程式之一,wmax是对应已选择的w方程式,在DBpedia图上全局最大的权值。
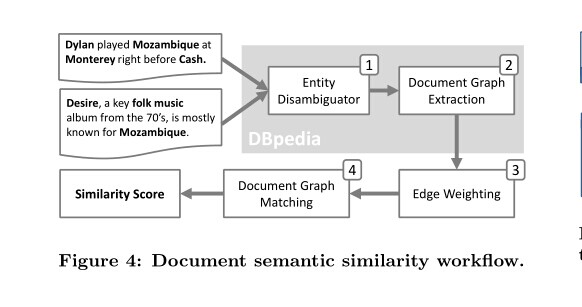
(3)最后,我们计算实体对之间的语义距离,也就是说,参照实体ref和Ecand中每一个候选实体轮流来比,取最短路:
我们对这些实体根据语义距离升序排序。两个实体间的每一条路径损耗就是有向边上的无向损耗的和(就是说图虽然是有向的,但是路径中计算权值时按无向来,译者注),我们有路径p:
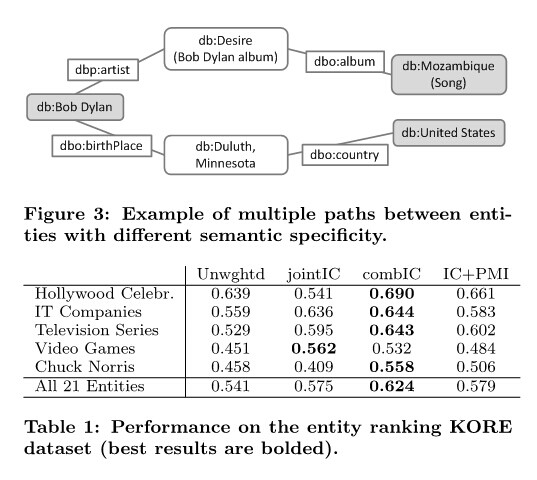
通过这个方法,我们能够在我们的后台知识库的基础上,通过语义距离的取反来决定任意两个实例间的相关程度。我们通过一个例子简单的叙述图3中我们的方法,db:Bob_Dylan和db:Mozambique_(Song) 作为输入实体对。考虑到实体db:Bob_Dylan(the musician),我们注意到他并不被直接连接到他的歌曲,db:Mozambique_(Song)。然而,多亏了DBpedia对非常特殊的事实进行了编码---也就是(i)Bob Dylan是专辑db:Desire_(Bob_Dylan_album)的主要艺术家,(ii)db:Mozambique_(Song)是这个同名专辑里的一首歌曲,从而我们估计出这两个输入实体间有着非常高的语义关联度。
注意到我们的加权方式在估计语义重叠度时起到了非常重要的作用。如果我们仔细看看的话,举个例子,对于另一对实体对,比如db:Bob_Dylan和db:United_States,我们发现在DBpedia里,这些实体被一些短的,信息量更少的(因为太具一般性),而且由单个中间实体(db:Duluth,_Minnesota)所连接。我们通过指派给边低的权值来来表示一般性的语义关系诸如dbo:birthPlace和dbo:country。非常棒的结果就是,我们可以将db:Mozambique_(Song)的排名排的更高于db:United_States,即使它们都通过等长度路径被连接到了参照实体db:Bob_Dylan。
实验配置与评估
我们从Hoffart拿到KORE实体排名数据集。这个数据集包含了来自4个域的21个不同的参照实体,这4个域分别是:IT公司,好莱坞庆典,电视连续剧,电子游戏。还有一个单独的数据集Chuck Norris。对每个排名问题,Hoffart选择一个拥有20个候选实体的集合,而且它们与参照实体之间的都有着区别度。相似度评估的方法来从人工判断到使用一系列的众包,可谓方法众多。举个例子,实体“Apple Inc.”(来自目录“IT Company”)和其他的实体组对:
参照实体:Apple Inc.
相关实体(排名):Steve Jobs(1),Steve Wozniak(2),...,Silicon Valley(9),NeXT(10),...,Ford Motor Company(20)
自然地,不同的实体与参照实体之间都有着不同的区别度。比如,“Steve Jobs”,排名最高,因为他曾是苹果公司首屈一指的关键人物。在排名的中间,我们发现相关的公司“NeXT”,这是被乔布斯发现的一家公司。最后,在排名末端,我们发现福特汽车公司,与苹果公司有很少的关联,虽然都是美国公司,但却属于另一个工业领域。
我们沿用Hoffart原始的评估配置,并且对每一个参照实体计算“Spearman”排名相关系数ρ,然后通过平均数据集里所有的参照实体得到全部结果。并且我们在表1中列出了我们的结果,并且我们在2.3节对比了不同的加权方式。我们使用DBpedia无向图,这样相当于将计算实体的相关性简化为了计算图网络里的距离方程。观察一下所有这三种可选择的加权方式,我们发现combIC始终优于基准,还有joinIC和IC+PMI。当我们观察特殊的域,jointIC并不能经常性的提高基准,相对于Chuck Norris和Hollywood celebrities这样的数据就显得非常差。但不管怎么样,整体平均地来看,这三种方式都不同程度的提高了基准,像combIC就平均提高了基准15.5%。当我们和Hoffart的原始结果比较时,我们方法的性能要略微低于最初的提议(ρ=0.673),但同时,优于它的近似值(ρ=0.621和0.425)。总的来说,我们用这些性能数据指出了在DBpedia上用权值路径来连通实体的优秀品质。因此,我们更进一步,使用这些路径对非结构化的数据提供一个结构化表述,这也就是自然语言文本。我们使用这些基于图的语义表述来计算文档间的语义相似度。
4. 计算文档相似度
我们提出了一种对我们的语义图的应用,目标是计算文本间的语义相似度。我们在图4中提供了对我们方法的一个概述,我们的方法从实体消歧后的结果开始,也就是从输入文本识别出一系列的概念。然后为了识别DBpedia的每一个被文档覆盖的子图,用连通路径来连接这些实体。语义网里的节点组成的概念可捕捉到文档里的主题,而且图里的边都被赋权值,用来识别那些相关联的概念间的语义关系。最后我们将计算语义相似度视为一个不同文档的概念间的匹配问题,并且用一个基于相似度度量的图编辑距离来识别文档概念间最“好”的连接路径。最终,我们可以得到两个文档间的相似度。
4.1 文档图构造
给定一个输入文本文档,我们首先通过识别它所包含的概念集合来语义化它。为了达到这个目的,通过文档实体连接系统,词和短语都被用DBpedia的概念所注释。给定一个短语和它的候选实体,实体连接器在文本里找到它的最近似意义,比如,像Spotlight,使用向量空间模型(基于一个词袋的方法)。因此,给定一个文档,我们获得消歧实体和它们的关联词语,短语的集合。在图5中的两个例子文档,比如我们提取了db:Bob_Dylan,db:Johnny_Cash和db:Desire_(Bob_Dylan_album).我们把这些提取出来的概念叫做文档图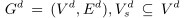
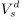
是通过2.2节描述的过程建立的,其中
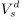
4.2 基于图文档的相似度
既然我们在第2章节中提出了将文档表示成赋权值的DBpedia子图,那么我们自然而然的将计算文档相似度转化成了一个图的匹配问题。尽管现在存在准确的图匹配算法,比如基于图同构,我们需要我们的度量方法能够有效的量化相似度。因此,我们选择图编辑距离技术来应对我们的特殊问题。
图编辑距离(GED)是一个一般的,非准确的图匹配方法,它通过计算从一个图转换为另一个图的最小编辑操作花费来定义两个图之间的距离。一般的,GED度量需要定义编辑花费方程,包括对节点和边的插入,删除,和更改。但是,给出我们特殊问题的设置,我们摒弃某些需求并且仅仅定义节点的花费方程。这是因为,给定一对语义图,根据第2节所讲的方法,这些实际上就组成了同样背景模型的两个子图,也就是DBpedia。这样一来,我们就不需要对边定义花费方程,若一条边在当前图中存在与否也同样会表现在另一个图里,将阐述了两个文档图属于同一个父图这样一个事实。所以,在边上的编辑操作将不会单独的发生,我们将边花费方程定义为0。
我们定义节点的花费操作将在下面讲述。因为我们的工作基于一个将概念表示为唯一URI的定义明确的本体,因此我们可以依赖节点在DBpedia图中是唯一的这样一个事实。这样我们就不需要考虑概念间的标签不匹配。例如:实体“Bob_Dylan”在图中被db:Robert_Allen_Zimmerman所识别,并且将它交付给db:Bob_Dylan,反之亦然。那么,与标准的图编辑距离方法所不同的是,我们给予潜在边的结构来定义节点的修改方式,也就是说,图中的加权距离,与基于字符串的相似度编辑距离度量方法截然不同。两个节点间的修改花费的定义类似于在第3节中提到的,连通路径上所有边的花费和。同样的道理,就是说,两个节点间越是语义相关,那么从节点1到节点2的花费也就越少。
对GED问题,一个准确的解决方案就是在所有可能的编辑操作中作树形搜索,但是对任一个合理规模的图来说,其计算性都是比较棘手的。在我们的工作中,故而我们使用一种近似方法,该方法基于二分图匹配,以此来寻找最小编辑花费。首先与计算出每个节点对最小编辑花费,然后将它们的花费存储在一个矩阵里。然而,两个节点间可能存在多条路径(也就是存在多个编辑花费值),我们则选择花费最小的节点修改操作来作为最小花费路径。接下来,再将矩阵扩展成含有插入和删除操作花费的矩阵。那么这个时候,计算GED便转化成了两个源图之间的二分图匹配问题,并且要服从一对一的匹配规则达到最小花费的目标(因为每一个节点只能被编辑一次)。我们利用匈牙利算法来解决这个最小限度问题。在计算过GED之后,我们应用一个简单标准化的步骤来消除不同图的影响,也就是文档大小问题。
我们总结算法如下(给定两个语义图Gi和Gj,来表示文档di和dj):
通过执行这个算法,便可以得到图Gi和Gj之间的图编辑距离。在我们的例子里,我们将得到从db:Bob_Dylan到db:Desire_(Bob_Dylan_album)的映射(cost 1.3) 和从db:Johnny_Cash到db:Folk_music的映射(cost 0.9+0.8)。最终相似度得分是这些编辑花费的和(3.0),接着再被两个文档里不同源实体的数量正规化(6)。
下面再附上原文:
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------












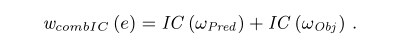
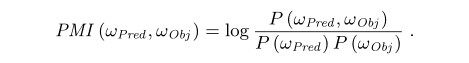
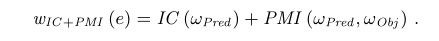
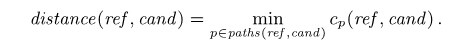
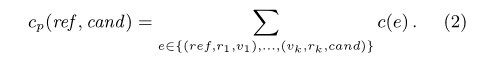

























 1609
1609

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








