信息熵这个概念相信对cs滴童鞋来说都不陌生,映象中在计算机网络,图像处理等课程中都各种接触,但是以前都仅仅只记住了p*log(1/P)这个公式,以及log(1/p)代表了信息量,然后在信号压缩技术中,如果信号的熵越大,信号的压缩率(原信号/压缩信号)越小这些大致的概念。而没有进一步去思考公式的含义或者说信息熵的由来。想想自己之前一切只为应付考试对知识不求甚解的心态真是令人汗颜。今天看书的时候又看到了熵这个概念,感慨熵的概念真是无处不在的同时,忍不住查了一下资料,重新认识了一下熵。
熵(entropy)的概念首次出现在热力学的研究中,用来度量热力学系统体系的随机性和无序性。对于熵在热力学中具体的解释和内容大家可以参见“熵”的百度百科内容,个人觉得总结地挺好的。随后,其他学科也将熵这个概念引入,用于表示改学科某种系统体系的混乱程度。1948年,香农在Bell System Technical Journal上发表了《通信的数学原理》(A Mathematical Theory of Communication)一文,将熵的概念引入信息论中。于是有了下面随处可见的信息熵公式:
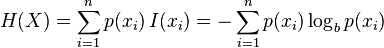
p 代表了 X 的机率质量函数,在这里 b 是对数所使用的底,通常是 2, 自然常数 e,或是10。当b = 2,熵的单位是bit;当b = e,熵的单位是 nat;而当 b = 10,熵的单位是 dit。
I(xi)表示xi这个事件本身的讯息(可以理解为xi所承载的信息量),可以看出I(xi)=-log p(xi),即xi出现的概率的对数函数的负。其实理解熵的关键就是理解 I(xi), 下面先给出最出名的一个计算I(xi) 的例子,然后再给出解释。
例: 英语有26个字母,假如每个字母在文章中出现次数平均的话,每个字母的信息量为:
看到这里,我们不禁想问,为什么每个字母所承载的信息量跟它出现的概率有关?为什么要取对数函数,而不是其他函数?最后,为什么需要取负?
首先,思考第一个问题,为什么会用到概率。我们需要回过头来看看,信息熵引入的意义,为了描述信息系统的混乱程度或者说该系统的确定性。那么如何描述呢?当然,我们得清楚信息系统中每一个“原子” (上例中的每一个字母)的状态。对于信息系统而言,为了知道整个体系的确定性,我们需要知道其中每个元素的确定性,而这个确定性不可避免的需要用到数学中的概率统计的相关概念来描述。举个例子,假设现在讨论的信息系统是一个txt文档,一个极端的情况,这个文档中文字全是“a”字母,那么,这个系统其实就只有一个元素--字母“a”,并且它出现的概率为1,容易看出我们讨论的这个信息系统可以说完全不混乱,是一个相当确定的系统。根据信息熵公式,我们可以得到该系统的熵为0并且“a”字母所承载的信息量为0,我们可以理解成“a”这个字母在这个系统中可以说是没有意义的,因为我们关心的是系统内容的有序性而不是系统内容的具体成分。
对于第二个问题,为什么要用对数函数。其实在回答第二个问题的同时可以进一步回答第一个问题。首先,我们需要注意到任意事件的概率有一个很重要的属性,概率取值必须介于[0,1]区间。再来看对数函数,它有一个很好的性质,值域可以很好的放大定义域处于[0,1]上的值,将[0,1]上的值映射到[0,∞],一个相当好的逆normalization过程。而我们知道要想知道整个系统的混杂程度,得研究每一个个体出现的概率分布,并由个体的概率分布来分析整个系统的行为。然而,概率值分布的区间太小,也就是说值与值之间的变化太小,特征不够明显。我们想要通过用每个个体的概率分布值来计算和比较不同系统之间混杂程度,最后得出的结果区分度必然不高,有些可能甚至需要精确到小数点后几十位才能比较,最后甚至可能会导致溢出而无法比较。所以为了让特征明确话,我们需要对原本的概率函数进行一些处理,让数值特之间的变化差距大一些,而对数函数则很好的可以帮助扩大区分度。这也是需要对概率取对数函数的原因。
最后,为什么要取负。其实很容易看出,如果某一个体发生的概率越小,说明它越有倾向杂质和噪声的可能,越容易导致系统混乱无序。因此,小概率个体实则对系统杂乱性和不确定性贡献越大,所以我们在处理个体概率时,不仅需要将其映射到更大的区间上以增大辨识度,还需要找个区间递减函数来映射之。综合以上,我们需要用递减的对数函数来处理个体概率,而一般我们习惯取2,e,10作为对数函数基底(查对数表方便)。可以看得对数函数曲线在基底大于的时候是增函数,为了让其变区间递减函数需要前面加负号。
最后的最后,熵是整个系统的平均消息量,即:

所以在熵计算公式中两次使用到概率,一个是用来反映个体发生概率对整个系统混杂程度的影响,另外一个是计算系统平均值的时候引进的。
-
- note:因为没有真正去看香浓提出熵的那篇论文,所以对于三个问题的回答纯属自己的理解,如有误,还请大家指正。
- ref: 熵(信息论)维基百科
- 熵-百度百科
-
-








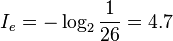















 5229
5229

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








