在OpenGL固定管线内容中有一个过程是进行视图变换,主要目的是将世界坐标变换到相机坐标空间中,OpenGL的视图变换所处的位置如下图所示:
在OSG中通过重写漫游器的时候需要实现的4个虚函数与这个变换是一致的(详细参考另一篇文章 《osg中漫游器的原理(一)》)
- 相机视图变换
在OpenGL中初始位置场景的世界坐标与相机坐标是在一起的,视点的方向是Z轴的负方向,
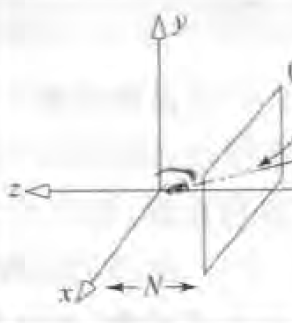
相机位置经过变换之后可以处于世界坐标系中的任何位置,可以通过两个变换:旋转和平移将相机移动到场景中的任意位置,如下图所示:
在OSG中如果定义自己的漫游器,需要实现的4个纯虚函数如下:
对应着图中 getMatrix获取的位置姿态矩阵是 R*T [将相机系统中的坐标变换到世界坐标系统中的坐标的矩阵], getInverseMatrxi则是将世界坐标变换为相机坐标的矩阵(称为视图矩阵,对应着
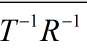 (使用的是OSG中前乘的方式来描述,如果是OpenGL,那么应该是 T*R)
(使用的是OSG中前乘的方式来描述,如果是OpenGL,那么应该是 T*R)
- 视图变换 uvn系统的推导
对于视图矩阵的推导,一般比较常用的是使用uvn系统的方式进行的,它的推导如下:
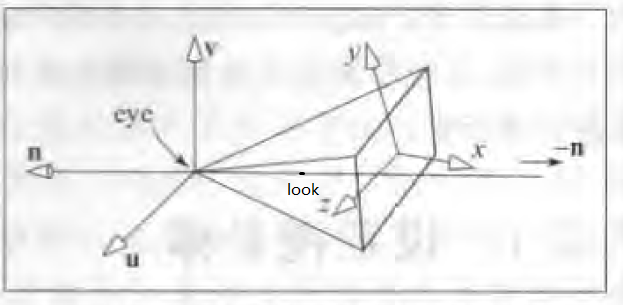
如上图所示,相机坐标系统的三个轴向是 uvn,其中u是向右的方向,v是向上的方向,-n是向前的方向,推导的方式如下,首先可以计算n的方向,n = eye - look(n是向量),知道n的方向,接下来需要求出u和v,由于u是垂直于n和v,也就是u垂直于n和v的平面,于是我们一般假设一个向上的方向up,但是这个up方向不能与n平行,通过up和n的叉乘得到u方向,得到u方向之后,通过n叉乘u得到真正相机的向上方向v,概括来说,也就是:
之后我们怎么进行变换计算出视图矩阵呢,相机在不同的坐标系统下的坐标是不同的,这不同的坐标值正是相机在不同基下的坐标,举个例子来说:
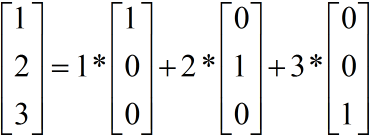
这里面
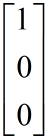 和
和
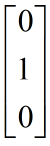 以及
以及
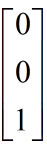 就是一个基,也就是最常见的(i,j,k)这种方式。
就是一个基,也就是最常见的(i,j,k)这种方式。
 和
和
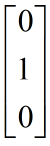 以及
以及
 就是一个基,也就是最常见的(i,j,k)这种方式。
就是一个基,也就是最常见的(i,j,k)这种方式。
下面我们以这个理论来推导视图矩阵,在初始状态的时候世界坐标系xyz和相机坐标系u0v0n0的各个轴向的方向相同,有如下的关系:
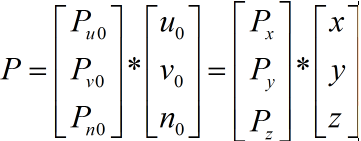
这里面P是空间坐标系中的一个向量, u0,v0,n0是相机坐标系的基,x,y,z是世界坐标系的基,初始状态二者是重合的,于是有:
pu0 = px, pv0 = py, pn0 = pz
相机和向量P都旋转之后,有以下关系:
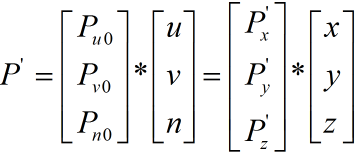
P‘ 是P同相机一起旋转后的向量, u,v,n是相机旋转后的基, Pu0,Pv0,Pn0是P’在它下面的坐标,因为P和相机是一起旋转的,所以坐标不变。x,y,z仍然是世界坐标的基,Px’,Py‘, Pz’是P‘在它下面的坐标,因为Px=Pu0, Py = Pv0, Pz = Pn0,所以有:
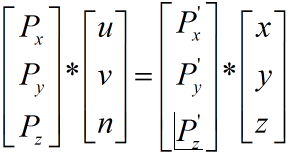
由于x,y,z是世界坐标系的基(单位矩阵),所以就有:
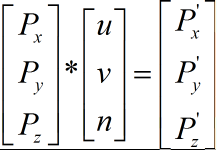
也就是说向量P(Px,Py,Pz)经过和相机一起旋转变成了坐标P’(Px‘,Py’,Pz‘),也是就
P* R = P’, 旋转矩阵就是R,也就是说 R正好等于:
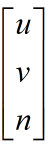
写成4x4矩阵形式就是:
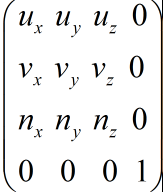
平移矩阵T很简单,
于是相机的位置姿态矩阵就是二者相乘, C = R * T =
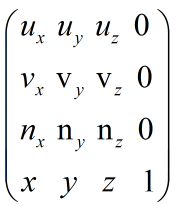
相机的位置姿态矩阵C是 将相机坐标系中点的坐标变换到世界坐标系统中 P‘ = P*C(P’是世界坐标系中的新的坐标),那么计算世界坐标系中的坐标在相机坐标系统下的坐标就应是 P = P‘ 乘以 C的逆矩阵,这样就得到了P’在相机坐标系统中的坐标,所以相机的视图矩阵是C的逆矩阵,也就是:
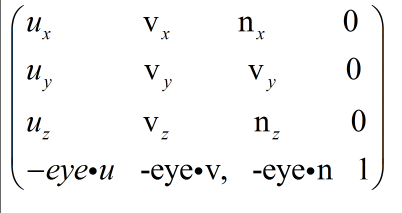
- 备注
本文中使用的推导是采用的行主序的方式进行的,使用列主序方式的推导应该最后得到的矩阵是与文中结论是转置的关系,下面详细说明一下,关于行主序和列主序,左乘右乘以及对OpenGL计算产生的影响,请查看另一篇文章
《OpenGL的列向量和OSG的行向量》
(1)行向量的方式(行主序)
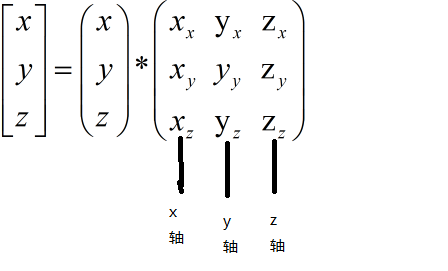
使用行主序的方式,那么三个坐标轴的值应该是横向的去写,也就是说
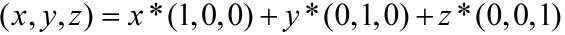
写成矩阵的形式应该是:
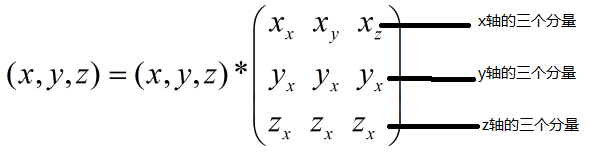
假设正好是世界坐标系,那么这三个分量正好就是(1,0,0)(0,1,0)和(0,0,1),也就是说如果是三个基坐标写成行向量的方式(横向),那么该方式就是行主序的方式,对应着在OSG中的方式,最终的视图矩阵的结论如本文中一致,是:
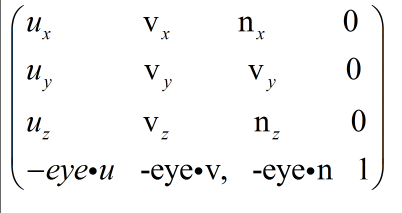
(1)列向量的方式(列主序)
使用列主序的方式,矩阵会变成为:
也就是说如果是三个基坐标写成列向量的方式(纵向),那么该方式就是列主序的方式,对应着在OpenGL中的方式,最终的视图矩阵的结论是本文推导矩阵的转置矩阵,也就是








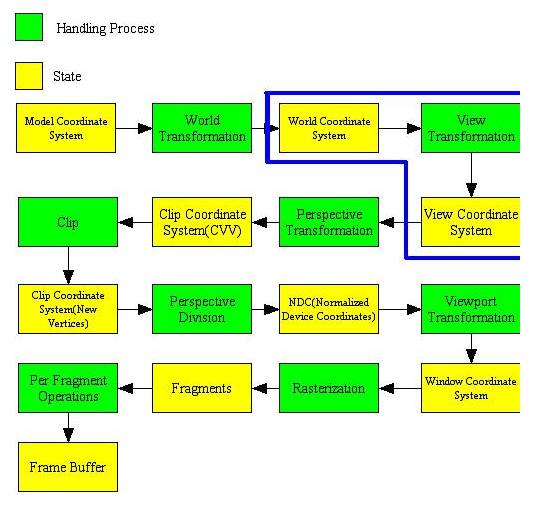

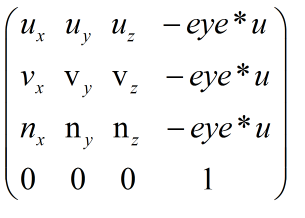














 930
930

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








