AUC的三种计算方法及代码

前言

AUC(Area Under Curve)，指的是ROC曲线(下图黄色的线)下的面积，ROC相关知识参见西瓜书。

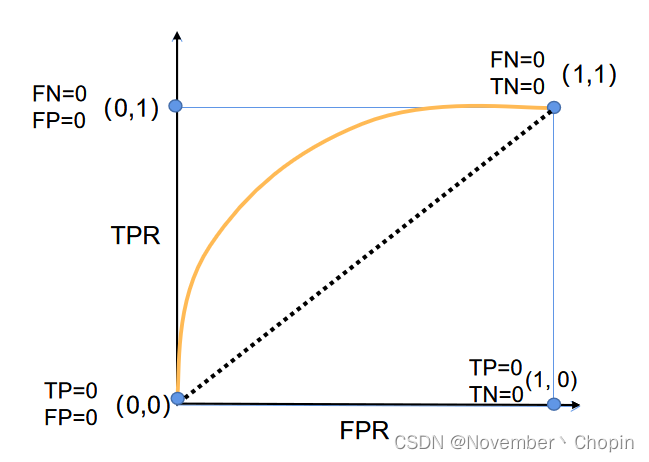
基于上述ROC曲线引申出AUC另外一个定义：正样本被预测成正样本的概率大于负样本被预测成正样本的概率的概率，如TPR=FPR这条线，AUC=0.5，即正样本被预测成正样本的概率等于与负样本被预测成正样本的概率。

本文参考了《深入浅出AUC系列一》，感觉这个博文说的不是太清晰，所以按照自己的思路重写了一遍，并添加了计算代码。

ROC的计算方法

基于上述的定义，AUC则有两种计算思路：

• 构建ROC曲线，计算曲线下的面积；
• 计算正样本预测为正样本概率排在负样本预测为正样本概率前面的概率，这样就转换成排序问题。

sklearn库提供了AUC的计算方法：sklearn.metrics.roc_auc_score(y_true, y_score)，参见scikit-learn 官方文档。

方法1: ROC曲线下的面积

首先需要将预测结果按概率从大到小排列成右上图。

再取不同的阈值(大于等于阈值)，得到每个预测样本属于TP/FP/FN/TN哪个类别

上述6个阈值获得6个(FPR,TPR)坐标点，连成的ROC曲线如下：

则AUC为ROC曲线下的面积(梯形面积+矩形面积)：
$$(\frac{1}{3}+\frac{2}{3})\times \frac{1}{2}÷2+1\times \frac{1}{2}=0.75$$。

方法2: 正样本得分大于负样本得分的概率

根据AUC的另外一个定义，AUC为正样本得分大于负样本得分的概率。步骤如下：

1. 选取所有正样本与负样本的两两组合
2. 计算正样本预测值pos_score大于负样本预测值neg_score的概率：
   • 如果pos_score>neg_score，概率为1
   • 如果pos_score==neg_score，概率为0.5
   • 如果pos_score<neg_score，概率为0

如果有$M$个正样本，$N$个负样本，则会产生$M\times N$个样本对，所以算法时间复杂度为$\mathcal{O}(M\times N)$。

实现代码如下：

注：下面的函数计算结果与sklearn.metrics.roc_auc_score一致，但在样本量为10000的时候，运行时间是后者的2000倍！

import numpy as np

y_true =  [0,   0,   1,   1,   0,   1,   0,   1,   1,   1]
y_score = [0.1, 0.4, 0.6, 0.6, 0.7, 0.7, 0.8, 0.8, 0.9, 0.9]

def get_roc_auc(y_true, y_score):
    gt_pred = list(zip(y_true, y_score))
    probs = []
    pos_samples = [x for x in gt_pred if x[0]==1]
    neg_samples = [x for x in gt_pred if x[0]==0]
    
    # 计算正样本大于负样本的概率
    for pos in pos_samples:
        for neg in neg_samples:
            if pos[1]>neg[1]:
                probs.append(1)
            elif pos[1]==neg[1]:
                probs.append(0.5)
            else:
                probs.append(0)
    return np.mean(probs)
print(get_roc_auc(y_true, y_score))

方法3: 改进方法2的计算

方法3是对方法2的改进，它舍弃了穷举正负样本对，而是先根据得分从小到大排序，然后找出每个正样本的排序位次。计算出每个位次下负样本的个数，就是该正样本得分大于负样本得分的次数，对次数进行累加就是所有正样本得分大于负样本得分的次数，除以$M\times N$ 就是所有正样本得分大于负样本得分的概率，如下图所示：

比如上图，有M=6个正样本，

• 对于 $rank=10$ 的正样本，它是正样本中预测得分第1高的样本，所以其下面有$M-1$个正样本，有$10-M$个负样本；
• 对于 $rank=9$ 的正样本，它是正样本中预测得分第2高的样本，所以其下面有$M-2$个正样本，有$9-(M-1)$个负样本；
• …
  以此类推，就可以算出所有正样本大于负样本得分的次数：
  $$[10-(M)]+[9-(M-1)]+...+[3-(M-5)]=\sum _{i\in 正样本}ran{k}_i-M(M+1)/2$$，除以$M\times N$，就可以得到AUC：
  $$AUC=\frac{{\sum }_{i\in 正样本}ran{k}_i-M(M+1)/2}{M\times N}$$，其中$M$为正样本数，$N$为负样本数， ${\sum }_{i\in 正样本}ran{k}_i$为正样本的序号之和；

由于需要对整个样本集进行排序，设$n=M+N$，所以算法的时间复杂度为$\mathcal{O}(nlogn)$。

代码如下：

注：下面的函数计算结果与sklearn.metrics.roc_auc_score一致，在样本量为10000的时候，运行时间是后者的3.7倍。

def get_roc_auc(y_true, y_score):
    ranks = enumerate(sorted(zip(y_true, y_score), key=lambda x:x[-1]), start=1)
    pos_ranks = [x[0] for x in ranks if x[1][0]==1]
    M = sum(y_true)
    N = len(y_true)-M
    auc = (sum(pos_ranks)-M*(M+1)/2)/(M*N)
    return auc

这里有个特殊情况在于当正负样本概率相等时，可能排在前面也可能在后面，如果单纯将正样本排在前面或者后面计算，计算结果与前面的会有偏差，这样的话则不建议用该公式直接计算。如果使用，需要对该公式进行特殊值处理。

附：sklearn.metrics.roc_auc_score计算auc

from sklearn.metrics import roc_auc_score
import numpy as np
pos_num = 169*2
neg_num = 16907
label = [float(x) for x in np.array([1]*pos_num+[0]*neg_num)]
pred = [float(x) for x in np.hstack([np.random.normal(1,1,pos_num), np.random.normal(0,1,neg_num)])]
auc = roc_auc_score(label, pred)
print(auc)
"""
0.7694951812613592
"""

AUC的spark实现（ing）

import numpy as np

# spark ml库代码
scoreAndLabels = spark.sparkContext.parallelize(list(zip(pred, label)))
from pyspark.mllib.evaluation import BinaryClassificationMetrics
metrics = BinaryClassificationMetrics(scoreAndLabels)
print("spark结果: ", metrics.areaUnderROC)

# sklearn验证
from sklearn.metrics import roc_auc_score
import numpy as np
print("sklearn结果: ", roc_auc_score(label, pred))

"""
spark结果:  0.7694995560467761
sklearn结果:  0.7694951812613592
"""

注意，在9万多条样本中的测试表明，BinaryClassificationMetrics相比于sklearn的roc_auc_score会有1e-6量级的误差。

总结

如果在本地使用的话，推荐sklearn.metrics.roc_auc_score，速度快；
如果在集群和大数据中使用，推荐方法3，很容易实现对HIVE表的操作。

【完】