注:本文中所有公式和思路来自于邹博先生的《机器学习升级版》,我只是为了加深记忆和理解写的本文。
上一篇文章算是比较详细的介绍了变分算法,本篇文章将会介绍一下一些变分框架在其他模型上的应用。
变分贝叶斯:
变分不光可以推测隐变量,还可以估计参数本身,我们可以使用平均场方法,将后验概率写成参数各自分布的乘积,既得到变分贝叶斯(Variational Bayesian, VB)
高斯分布的变分贝叶斯:
我们使用变分贝叶斯推断一维高斯分布p(μ, σ2 | D)后验概率的参数,用λ来替代σ2的导数,又称λ为精度:
为了方便计算,使用共轭先验的形式:
我们可以看成是混合高斯分布GMM,因为高斯分布的均值的共轭先验分布仍然是高斯分布,方差的共轭先验分布式伽马分布。那么我们可以近似分解成:
目标函数
我们首先给定几个超参数a,b,κ,μ,那么则有:
将这几个分布带入目标函数:
既然得到上边的结果,接下来我们就要进行参数估计了,根据变分的思想,我们估计一个参数,是试用其他参数来进行求期望得到的,那么就先更新μ:
我们可以通过对比高斯分布的对数形式:
计算得到:
接着更新λ:
通过对比Gamma分布对数形式:
得到:
同时:
将结果带入公式,根据:
以及:
得到:
这就是更新过程,公式虽然多一点,都没啥新东西,比较简单。
变分总结
变分既能够推断隐变量,也能推断未知参数,是很有力的参数估计工具。难点在于推导复杂。
相对于采样,变分不容易计算但是效率很高。
平均场方法的变分推导,对离散和连续的隐变量都适用,在平均场方法的框架下,变分推导一次更新一个分布,其本质是坐标上升。
变分除了和贝叶斯结合得到VB,还可以和EM算法结合,得到VBEM,用于带隐变量和未知参数的估计,如GMM、LDA
到此变分算法就全部介绍完了,欢迎批评指正。








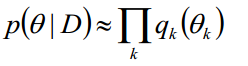

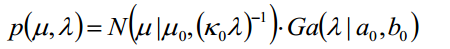
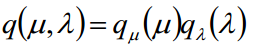
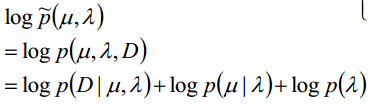
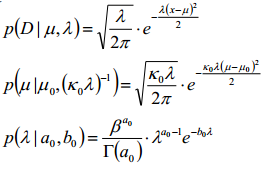
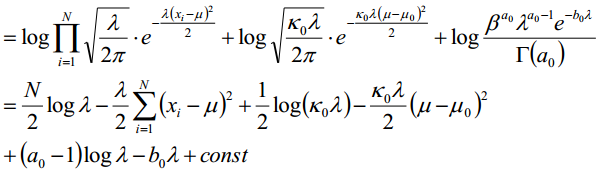
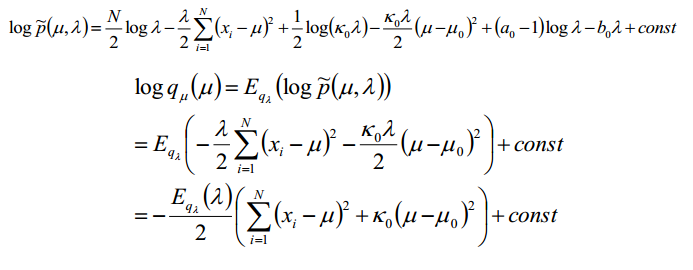
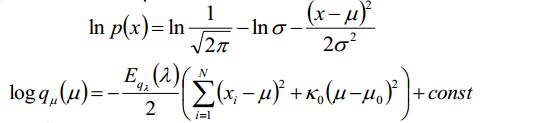
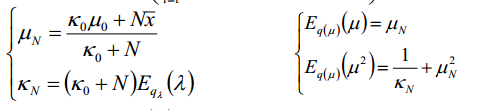
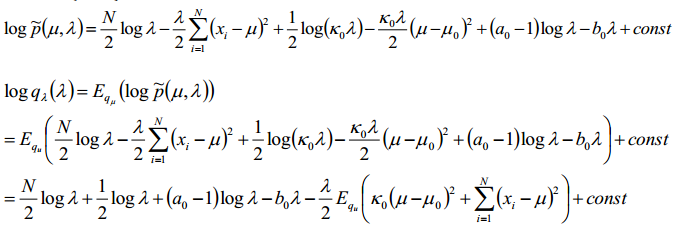
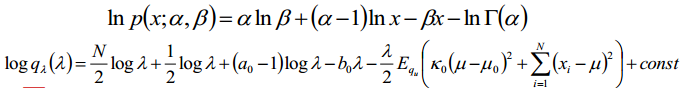
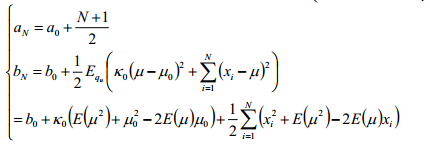
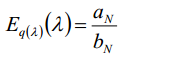
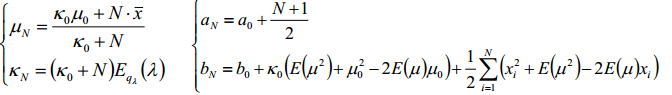
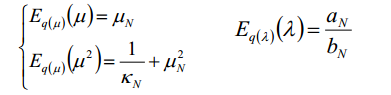
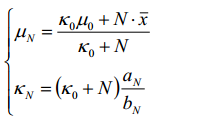














 9032
9032

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








