变分（Calculus of variations）的概念及运算规则（二）

---

6. Euler-Lagrange equation

6.6 一般化

• 具有更高导数的单变量单函数

泛函的平稳值：

$$I[f]={\int }_{x_0}^{x_1}\mathcal{L}(x,f,f^{\prime },f^{\prime \prime },\dots ,f^{(k)})\mathrm{d}x;f^{\prime }:=\frac{\mathrm{d}f}{\mathrm{d}x},f^{\prime \prime }:=\frac{{\mathrm{d}}^{2}f}{\mathrm{d}{x}^2},f^{(k)}:=\frac{{\mathrm{d}}^{k}f}{\mathrm{d}{x}^k}$$

可以从欧拉-拉格朗日方程得到：

$$\frac{\partial \mathcal{L}}{\partial f}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial \mathcal{L}}{\partial f^{\prime }}\right)+\frac{{\mathrm{d}}^2}{\mathrm{d}{x}^2}\left(\frac{\partial \mathcal{L}}{\partial f^{\prime \prime }}\right)-\cdots +(-1{)}^k\frac{{\mathrm{d}}^k}{\mathrm{d}{x}^k}\left(\frac{\partial \mathcal{L}}{\partial f^{(k)}}\right)=0$$

在函数本身以及第一个 $k-1$ 导数的固定边界条件下（即对于所有 f ( i ) , i ∈ { 0 , . . . , k − 1 } f^{(i)},i\in \{0,... ,k-1\} f(i),i∈{0,...,k−1}）。最高导数 $f^{(k)}$ 的端点值保持灵活。

• 具有单导数的单变量的多个函数

如果问题涉及找到单个独立变量 $(x)$ 的多个函数 $(f_1,f_2,\dots ,f_m)$ ，其都在泛函的极值上：

$$I[f_1,f_2,\dots ,f_m]={\int }_{x_0}^{x_1}\mathcal{L}(x,f_1,f_2,\dots ,f_m,f_1^{\prime },f_2^{\prime },\dots ,f_m^{\prime })\mathrm{d}x;f_i^{\prime }:=\frac{\mathrm{d}{f}_i}{\mathrm{d}x}$$

那么对应的欧拉-拉格朗日方程为：

$$\begin{array}{r}\frac{\partial \mathcal{L}}{\partial f_i}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial \mathcal{L}}{\partial f_i^{\prime }}\right)=0;i=1,2,...,m\end{array}$$

• 具有单导数的多变量的单函数

多维泛化来自考虑 $n$ 个变量的函数。如果 $\Omega$ 是某个曲面，那么：

$$I[f]={\int }_{\Omega }\mathcal{L}(x_1,\dots ,x_n,f,f_1,\dots ,f_n)\mathrm{d}\mathbf{x};f_j:=\frac{\partial f}{\partial x_j}$$

仅当 $f$ 满足偏微分方程时才被取极值：

$$\frac{\partial \mathcal{L}}{\partial f}-\sum _{j=1}^n\frac{\partial }{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_j}\right)=0$$

当 $n=2$ 且泛函 $\mathcal{I}$ 是能量泛函时，这会导致肥皂膜最小表面问题（Minimal surface）。

• 具有单导数的多变量的多个函数

如果要确定多个多变量的未知函数，使得

$$I[f_1,f_2,\dots ,f_m]={\int }_{\Omega }\mathcal{L}(x_1,\dots ,x_n,f_1,\dots ,f_m,f_{1,1},\dots ,f_{1,n},\dots ,f_{m,1},\dots ,f_{m,n})\mathrm{d}\mathbf{x};f_{i,j}:=\frac{\partial f_i}{\partial x_j}$$

那么欧拉-拉格朗日方程为：

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial f_1}-\sum _{j=1}^n\frac{\partial }{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{1,j}}\right)& =0_1\\ \frac{\partial \mathcal{L}}{\partial f_2}-\sum _{j=1}^n\frac{\partial }{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{2,j}}\right)& =0_2\\ ⋮⋮& ⋮\\ \frac{\partial \mathcal{L}}{\partial f_m}-\sum _{j=1}^n\frac{\partial }{\partial x_j}\left(\frac{\partial \mathcal{L}}{\partial f_{m,j}}\right)& =0_m.\end{array}$$

• 具有更高导数的两个变量的单函数

如果要确定一个未知函数 $f$，它取决于两个变量 $x_1$ 和 $x_2$，并且如果函数取决于 $f$ 的高阶导数，直到 $n$，使得

$$\begin{array}{rl}I[f]& ={\int }_{\Omega }\mathcal{L}(x_1,x_2,f,f_1,f_2,f_{11},f_{12},f_{22},\dots ,f_{22\dots 2})\mathrm{d}\mathbf{x}\\ & f_i:=\frac{\partial f}{\partial x_i},f_{ij}:=\frac{{\partial }^{2}f}{\partial x_i\partial x_j},\dots \end{array}$$

那么欧拉-拉格朗日方程为：

$$\begin{array}{rl}\frac{\partial \mathcal{L}}{\partial f}& -\frac{\partial }{\partial x_1}\left(\frac{\partial \mathcal{L}}{\partial f_1}\right)-\frac{\partial }{\partial x_2}\left(\frac{\partial \mathcal{L}}{\partial f_2}\right)+\frac{{\partial }^2}{\partial x_1^2}\left(\frac{\partial \mathcal{L}}{\partial f_{11}}\right)+\frac{{\partial }^2}{\partial x_1\partial x_2}\left(\frac{\partial \mathcal{L}}{\partial f_{12}}\right)+\frac{{\partial }^2}{\partial x_2^2}\left(\frac{\partial \mathcal{L}}{\partial f_{22}}\right)\\ & -\cdots +(-1{)}^n\frac{{\partial }^n}{\partial x_2^n}\left(\frac{\partial \mathcal{L}}{\partial f_{22\dots 2}}\right)=0\end{array}$$

这可以简单地表示为：

$$\frac{\partial \mathcal{L}}{\partial f}+\sum _{j=1}^n\sum _{{\mu }_1\le \dots \le {\mu }_j}(-1{)}^j\frac{{\partial }^j}{\partial x_{{\mu }_1}\dots \partial x_{{\mu }_j}}\left(\frac{\partial \mathcal{L}}{\partial f_{{\mu }_1\dots {\mu }_j}}\right)=0$$

其中 ${\mu }_1\dots {\mu }_j$ 是变量数量的索引，也就是说，它们从 $1$ 到 $2$。这里对 ${\mu }_1\dots {\mu }_j$ 索引的求和仅在 ${\mu }_1\le {\mu }_2\le \dots \le {\mu }_j$，这是为了避免多次计算相同的偏导数，例如 $f_{12}=f_{21}$ 在前面的等式中只出现一次.

• 具有更高导数的多变量的多个函数

如果有 $p$个取决于 $m$ 个变量 $x_1,\cdots ,x_m$ 的未知函数 $f_i$ 被确定，并且如果函数取决于 $f_i$ 的高阶导数，直到第 $n$ 阶，使得：

$$\begin{array}{rl}I[f_1,\dots ,f_p]& ={\int }_{\Omega }\mathcal{L}(x_1,\dots ,x_m;f_1,\dots ,f_p;f_{1,1},\dots ,f_{p,m};f_{1,11},\dots ,f_{p,mm};\dots ;f_{p,1\dots 1},\dots ,f_{p,m\dots m})\mathrm{d}\mathbf{x}\\ & f_{i,\mu }:=\frac{\partial f_i}{\partial x_{\mu }},f_{i,{\mu }_1{\mu }_2}:=\frac{{\partial }^2{f}_i}{\partial x_{{\mu }_1}\partial x_{{\mu }_2}},\dots \end{array}$$

其中 ${\mu }_1\dots {\mu }_j$ 是变量数量的索引，即它们从 $1$ 到 $m$。那么欧拉-拉格朗日方程为：

$$\frac{\partial \mathcal{L}}{\partial f_i}+\sum _{j=1}^n\sum _{{\mu }_{1}leq\dots \le {\mu }_j}(-1{)}^j\frac{{\partial }^j}{\partial x_{{\mu }_1}\dots \partial x_{m{u}_j}}\left(\frac{\partial \mathcal{L}}{\partial f_{i,{\mu }_1\dots {\mu }_j}}\right)=0$$

其中 ${\mu }_1\dots {\mu }_j$ 的求和避免计算相同的导数 $f_{i,{\mu }_1{\mu }_2}=f_{i,{\mu }_2{\mu }_1}$ 多次，就像上一小节一样。这可以更紧凑地表示为：

$$\sum _{j=0}^n\sum _{{\mu }_1\le \dots \le {\mu }_j}(-1{)}^j{\partial }_{{\mu }_1\dots {\mu }_j}^j\left(\frac{\partial \mathcal{L}}{\partial f_{i,{\mu }_1\dots {\mu }_j}}\right)=0$$

6.7 泛化到流形

令 $M$ 为光滑流形，令 $C^{\infty }([a,b])$ 表示光滑函数空间 $f:[a,b]\to M$。那么，对于泛函 $S:C^{\infty }([a,b])\to \mathbb{R}$ 的形式

$$S[f]={\int }_a^b(L\circ \dot{f})(t)$$

其中 $L:TM\to \mathbb{R}$ 是拉格朗日函数（Lagrangian），表述 $\mathrm{d}{S}_f=0$ 等价于这样的表述，对于所有 $t\in [a,b]$，$\dot{f}(t)$ 的邻域的每个坐标系平凡化（trivialization） $(x^i,X^i)$ ， 产生以下 $\dim M$ 方程：

$$\forall i:\frac{\mathrm{d}}{\mathrm{d}t}\frac{\partial L}{\partial X^i}{|}_{\dot{f}(t)}=\frac{\partial L}{\partial x^i}{|}_{\dot{f}(t)}$$

6.8 具体例子

为了说明这个过程，考虑寻找极值函数 $y=f(x)$ 的问题，它是连接两点 $(x_1,y_1)$ 和 $(x_2,y_2)$ 的最短曲线。曲线的弧长由下式给出：

$$A[y]={\int }_{x_1}^{x_2}\sqrt{1+[y^{\prime }(x){]}^2}\mathrm{d}x$$

和

$$y^{\prime }(x)=\frac{\mathrm{d}y}{\mathrm{d}x},y_1=f(x_1),y_2=f(x_2)$$

请注意，假设 $y$ 是 $x$ 的函数会失去一般性；理想情况下，两者都应该是其他一些参数的函数。这种方法仅用于说明目的。

现在将使用欧拉-拉格朗日方程来求极值函数 $f(x)$，它使函数 $A[y]$ 最小：

$$\frac{\partial L}{\partial f}-\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial L}{\partial f^{\prime }}=0$$

和

$$L=\sqrt{1+[f^{\prime }(x){]}^2}$$

由于 $f$ 没有显式出现在 $L$ 中，所以欧拉-拉格朗日方程中的第一项对于所有 $f(x)$ 都消失了，因此：

$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial L}{\partial f^{\prime }}=0$$

代入 $L$ 表达式并求导：

$$\frac{\mathrm{d}}{\mathrm{d}x}\frac{f^{\prime }(x)}{\sqrt{1+[f^{\prime }(x){]}^2}}=0$$

因此

$$\frac{f^{\prime }(x)}{\sqrt{1+[f^{\prime }(x){]}^2}}=c$$

$c$ 为积分常数。然后将上式左右平方：

$$\frac{[f^{\prime }(x){]}^2}{1+[f^{\prime }(x){]}^2}=c^2$$

其中：

$$0\le c^2<1$$

求解前式，我们得到：

$$[f^{\prime }(x){]}^2=\frac{c^2}{1-c^2}$$

这意味着

$$f^{\prime }(x)=m$$

是一个常数，因此连接两点的最短曲线 $(x_1,y_1)$ 和 $(x_2,y_2)$ 是：

$$f(x)=mx+b\text{with}m=\frac{y_2-y_1}{x_2-x_1}\text{and}b=\frac{x_2{y}_1-x_1{y}_2}{x_2-x_1}$$

因此我们找到了极值函数 $f(x)$，它最小化了泛函 $A[y]$ 使得 $A[f]$ 是最小值。直线方程是 $y=f(x)$。换句话说，换句话说，两点之间的最短距离是一条直线。

7. Beltrami’s identity

以 Eugenio Beltrami 命名的 Beltrami 恒等式是变分法中欧拉-拉格朗日方程的一个特例。

Euler-Lagrange 方程用于使以下形式的作用泛函极值化：

$$I[y]={\int }_a^{b}L[x,y(x),y^{\prime }(x)]dx$$

其中 $a$ 和 $b$ 是常数：

$$y^{\prime }(x)=\frac{dy}{dx}$$

如果 $\frac{\partial L}{\partial x}=0$，则欧拉-拉格朗日方程简化为 Beltrami identity：

$$L-f^{\prime }\frac{\partial L}{\partial f^{\prime }}=C$$

其中 $C$ 是一个常数。左侧是 $L$ 相对于 $f^{\prime }(x)$。

这个结果背后的直觉是，如果变量 $x$ 实际上是时间，那么语句 $\frac{\partial L}{\partial x}=0$ 意味着拉格朗日函数是时间无关的。根据 Noether’s theorem，有一个相关的守恒量。在这种情况下，这个量是哈密顿量，拉格朗日量的勒让德变换，它（通常）与系统的能量一致。这又对应（减去）Beltrami’s identity 中的常数。

• 推导

根据链式法则，$L$ 的导数为

$$\frac{\mathrm{d}L}{\mathrm{d}x}=\frac{\partial L}{\partial x}\frac{\mathrm{d}x}{\mathrm{d}x}+\frac{\partial L}{\partial f}\frac{\mathrm{d}f}{\mathrm{d}x}+\frac{\partial L}{\partial f^{\prime }}\frac{\mathrm{d}{f}^{\prime }}{\mathrm{d}x}$$

因为 $\frac{\partial L}{\partial x}=0$，上式可以简化为：

$$\frac{\mathrm{d}L}{\mathrm{d}x}=\frac{\partial L}{\partial f}{f}^{\prime }+\frac{\partial L}{\partial f^{\prime }}{f}^{\prime \prime }$$

然后通过将其与欧拉-拉格朗日方程结合：

$$\frac{\partial L}{\partial f}=\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial L}{\partial f^{\prime }}$$

我们得到以下表达式：

$$\frac{\mathrm{d}L}{\mathrm{d}x}=f^{\prime }\frac{\mathrm{d}}{\mathrm{d}x}\frac{\partial L}{\partial f^{\prime }}+f^{\prime \prime }\frac{\partial L}{\partial f^{\prime }}$$

根据乘积法则，右边等价于：

$$\frac{\mathrm{d}L}{\mathrm{d}x}=\frac{\mathrm{d}}{\mathrm{d}x}\left(f^{\prime }\frac{\partial L}{\partial f^{\prime }}\right)$$

通过去掉微分，并将等式两边内容放在一边，我们得到了 Beltrami identity：

$$L-f^{\prime }\frac{\partial L}{\partial f^{\prime }}=C$$

• brachistochrone problem（最速降线问题）的解决方案

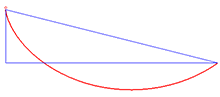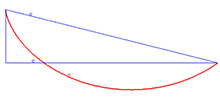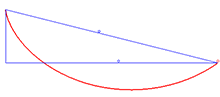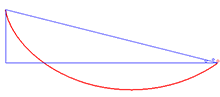
应用 Beltrami identity 的一个例子是 brachistochrone 问题，它涉及找到使积分最小化的曲线 $y=y(x)$：

$$I[y]={\int }_0^a\sqrt{\frac{1+y^{\prime 2}}{y}}\mathrm{d}x$$

被积函数：

$$L(y,y^{\prime })=\sqrt{\frac{1+y^{\prime 2}}{y}}$$

明确地不依赖于积分变量 $x$，所以 Beltrami identity 适用：

$$L-y^{\prime }\frac{\partial L}{\partial y^{\prime }}=C$$

代入 $L$ 并化简：

$$y(1+y^{\prime 2})=1/C^2(const.)$$

可以用参数方程形式的结果来求解：

$$\begin{gathered} x=A(\varphi -\sin \varphi ) \\ y=A(1-\cos \varphi ) \end{gathered}$$

$A$ 是上述常数的一半，$\frac{1}{2C^2}$，并且 $\varphi$ 是一个变量。这些是摆线的参数方程。

8. Euler–Poisson equation

如果 $S$ 取决于 $y(x)$ 的高阶导数，即，如果

$$S={\int }_a^{b}f(x,y(x),y^{\prime }(x),\dots ,y^{(n)}(x))\mathrm{d}x$$

那么 $y$ 必须满足欧拉-泊松方程：

$$\frac{\partial f}{\partial y}-\frac{\mathrm{d}}{\mathrm{d}x}\left(\frac{\partial f}{\partial y^{\prime }}\right)+\cdots +(-1{)}^n\frac{{\mathrm{d}}^n}{\mathrm{d}{x}^n}\left[\frac{\partial f}{\partial y^{(n)}}\right]=0$$

9. Du Bois-Reymond’s theorem

到目前为止的讨论假设极值函数具有两个连续导数，尽管积分 $J$ 的存在只需要试探函数（trial functions）的一阶导数。第一变分在极值处消失的条件可视为欧拉-拉格朗日方程的弱形式（weak form）。Du Bois-Reymond 定理断言，这种弱形式蕴含着强形式（strong form）。如果 $L$ 关于它的所有参数具有连续的一阶和二阶导数，并且如果

$$\frac{{\partial }^{2}L}{\partial f^{\prime 2}}\ne 0$$

那么 $f$ 有两个连续导数，并且满足欧拉-拉格朗日方程。

10. Lavrentiev phenomenon

希尔伯特是第一个为欧拉-拉格朗日方程提供良好条件的人，以给出一个平稳解。在凸区域和正三次可微拉格朗日内，解由可数的部分组成，这些部分要么沿着边界移动，要么满足内部的欧拉-拉格朗日方程。

然而，拉夫伦季耶夫在 1926 年表明，在某些情况下，没有最佳解决方案，但可以通过增加截面数量来任意接近解决方案。 Lavrentiev 现象确定了不同类别的可接受函数之间最小化问题的下确界的差异。例如以下问题，由 Manià 在 1934 年提出：[18]

{\displaystyle L[x]=\int _{0}^{1}(x{3}-t)^{2}x’{6},}{\displaystyle L[x]=\int _ {0}^{1}(x{3}-t)^{2}x’{6},}
{\displaystyle {A}={x\in W^{1,1}(0,1):x(0)=0,\ x(1)=1}.}{\displaystyle {A}= {x\in W^{1,1}(0,1):x(0)=0,\x(1)=1}.}
显然，{\displaystyle x(t)=t^{\frac {1}{3}}}{\displaystyle x(t)=t^{\frac {1}{3}}} 最小化了泛函，但我们找到任何函数 {\displaystyle x\in W^{1,\infty }}{\displaystyle x\in W^{1,\infty }} 给出一个远离下确界的值。

示例（一维）传统上表现为 {\displaystyle W^{1,1}}W{{1,1}} 和 {\displaystyle W^{1,\infty },}{\displaystyle W^ {1,\infty },} 但 Ball 和 Mizel[19] 获得了第一个在 {\displaystyle W^{1,p}}W{1,p} 和 {\displaystyle W^{1 ,q}}{\displaystyle W^{1,q}} 对于 {\displaystyle 1\leq p<q<\infty .}{\displaystyle 1\leq p<q<\infty .} 有几个结果给出不发生该现象的标准——例如“标准增长”、不依赖于第二个变量的拉格朗日函数或满足 Cesari 条件 (D) 的近似序列——但结果通常是特定的，适用于一小类泛函。

与拉夫连季耶夫现象相关的是排斥性：任何表现拉夫连季耶夫现象的泛函都会表现出弱排斥性。 [20]

11. Functions of several variables（多元函数）

例如，如果 {\displaystyle \varphi (x,y)}{\displaystyle \varphi (x,y)} 表示在 {\displaystyle x,y} x,y 平面，则其势能与其表面积成正比：

{\displaystyle U[\varphi ]=\iint _{D}{\sqrt {1+\nabla \varphi \cdot \nabla \varphi }},dx,dy.}{\displaystyle U[\varphi ]= \iint _{D}{\sqrt {1+\nabla \varphi \cdot \nabla \varphi }},dx,dy.}
Plateau 的问题包括找到一个函数，该函数在假设 {\displaystyle D}D 边界上的规定值的同时使表面积最小化；这些解称为最小曲面。这个问题的欧拉-拉格朗日方程是非线性的：
{\displaystyle \varphi _{xx}(1+\varphi _{y}^{2})+\varphi _{yy}(1+\varphi _{x}^{2})-2\varphi _{ x}\varphi _{y}\varphi _{xy}=0.}{\displaystyle \varphi _{xx}(1+\varphi _{y}^{2})+\varphi _{yy}(1 +\varphi _{x}^{2})-2\varphi _{x}\varphi _{y}\varphi _{xy}=0.}
有关详细信息，请参见 Courant (1950)。

狄利克雷原理
通常只考虑膜的小位移就足够了，其与无位移的能量差近似为

{\displaystyle V[\varphi ]={\frac {1}{2}}\iint _{D}\nabla \varphi \cdot \nabla \varphi ,dx,dy.}{\displaystyle V[\varphi ]={\frac {1}{2}}\iint {D}\nabla \varphi \cdot \nabla \varphi ,dx,dy.}
在所有假设 {\displaystyle D.}D 边界上的规定值的试验函数 {\displaystyle \varphi }\varphi 中，函数 {\displaystyle V}V 将被最小化。如果 {\displaystyle u}u 是最小化函数且 {\displaystyle v}v 是在 {\displaystyle D,}D 的边界上消失的任意平滑函数，那么 {\displaystyle V[u+\varepsilon v]}V[u+\varepsilon v] 必须消失：
{\displaystyle \left.{\frac {d}{d\varepsilon }}V[u+\varepsilon v]\right|{\varepsilon =0}=\iint {D}\nabla u\cdot \nabla v ,dx,dy=0.}{\displaystyle \left.{\frac {d}{d\varepsilon }}V[u+\varepsilon v]\right|{\varepsilon =0}=\iint _{ D}\nabla u\cdot \nabla v,dx,dy=0.}
假设 u 有两个导数，我们可以应用散度定理得到
{\displaystyle \iint _{D}\nabla \cdot (v\nabla u),dx,dy=\iint _{D}\nabla u\cdot \nabla v+v\nabla \cdot \nabla u\ ,dx,dy=\int _{C}v{\frac {\partial u}{\partial n}},ds,}{\displaystyle \iint _{D}\nabla \cdot (v\nabla u ),dx,dy=\iint _{D}\nabla u\cdot \nabla v+v\nabla \cdot \nabla u,dx,dy=\int _{C}v{\frac {\部分 u}{\partial n}},ds,}
其中 {\displaystyle C}C 是 {\displaystyle D,}D 的边界，{\displaystyle s}s 是沿 {\displaystyle C}C 和 {\displaystyle \partial u/\partial n}{\displaystyle \ partial u/\partial n} 是 {\displaystyle u}u 在 {\displaystyle C.}{\displaystyle C.} 上的正态导数。因为 {\displaystyle v}v 在 {\displaystyle C}C 上消失，第一个变体消失，结果是
{\displaystyle \iint _{D}v\nabla \cdot \nabla u,dx,dy=0}{\displaystyle \iint _{D}v\nabla \cdot \nabla u,dx,dy= 0}
对于在 {\displaystyle D.}D 的边界上消失的所有平滑函数 v。一维积分情况的证明可以适用于这种情况，以表明
{\displaystyle \nabla \cdot \nabla u=0}{\displaystyle \nabla \cdot \nabla u=0}
在 {\displaystyle D.}D.
这种推理的困难在于假设最小化函数 u 必须有两个导数。黎曼认为，平滑最小化函数的存在是通过与物理问题的联系来保证的：膜确实假设具有最小势能的配置。黎曼将这个想法命名为狄利克雷原理，以纪念他的老师彼得·古斯塔夫·勒琼·狄利克雷。然而，Weierstrass 给出了一个没有解决方案的变分问题的例子：最小化

{\displaystyle W[\varphi ]=\int _{-1}^{1}(x\varphi ')^{2},dx}{\displaystyle W[\varphi ]=\int _{-1} ^{1}(x\varphi ')^{2},dx}
在所有满足 {\displaystyle \varphi (-1)=-1}\varphi (-1)=-1 和 {\displaystyle \varphi (1)=1.}\varphi 的函数中 {\displaystyle \varphi }\varphi (1)=1。 {\displaystyle W}W 可以通过选择在原点的一个小邻域中在 -1 和 1 之间进行转换的分段线性函数来任意小。然而，没有任何函数使得 {\displaystyle W=0.}{\displaystyle W=0.}[j] 最终证明了狄利克雷原理是有效的，但它需要对椭圆部分的正则性理论进行复杂的应用微分方程;见 Jost 和 Li-Jost (1998)。

推广到其他边值问题
膜的势能更一般的表达式是

{\displaystyle V[\varphi ]=\iint _{D}\left[{\frac {1}{2}}\nabla \varphi \cdot \nabla \varphi +f(x,y)\varphi \right] ,dx,dy,+\int _{C}\left[{\frac {1}{2}}\sigma (s)\varphi ^{2}+g(s)\varphi \right]\ ,ds.}{\displaystyle V[\varphi ]=\iint _{D}\left[{\frac {1}{2}}\nabla \varphi \cdot \nabla \varphi +f(x,y)\ varphi \right],dx,dy,+\int _{C}\left[{\frac {1}{2}}\sigma (s)\varphi ^{2}+g(s)\varphi \right],ds.}
这对应于 {\displaystyle D,}D 中的外力密度 {\displaystyle f(x,y)}f(x,y)，边界上的外力 {\displaystyle g(s)}g(s) {\displaystyle C,}{\displaystyle C,} 和模量 {\displaystyle \sigma (s)}{\displaystyle \sigma (s)} 作用于 {\displaystyle C.}{\displaystyle C.}将势能最小化且对其边界值没有限制的函数将用 {\displaystyle u.}u 表示。假设 {\displaystyle f}f 和 {\displaystyle g}g 是连续的，正则性理论意味着最小化函数 {\displaystyle u}u 将有两个导数。在采用第一种变化时，不需要对增量 {\displaystyle v.}v 施加边界条件。 {\displaystyle V[u+\varepsilon v]}V[u+\varepsilon v] 的第一个变体由下式给出
{\displaystyle \iint _{D}\left[\nabla u\cdot \nabla v+fv\right],dx,dy+\int _{C}\left[\sigma uv+gv\right], ds=0.}{\displaystyle \iint _{D}\left[\nabla u\cdot \nabla v+fv\right],dx,dy+\int _{C}\left[\sigma uv+gv \right],ds=0.}
如果我们应用散度定理，结果是
{\displaystyle \iint _{D}\left[-v\nabla \cdot \nabla u+vf\right],dx,dy+\int _{C}v\left[{\frac {\partial u} {\partial n}}+\sigma u+g\right],ds=0.}{\displaystyle \iint _{D}\left[-v\nabla \cdot \nabla u+vf\right], dx,dy+\int _{C}v\left[{\frac {\partial u}{\partial n}}+\sigma u+g\right],ds=0.}
如果我们首先在 {\displaystyle C,}{\displaystyle C,} 上设置 {\displaystyle v=0}v=0，那么边界积分就消失了，我们像以前一样得出结论
{\displaystyle -\nabla \cdot \nabla u+f=0}{\displaystyle -\nabla \cdot \nabla u+f=0}
在 {\displaystyle D.}D.那么如果我们允许 {\displaystyle v}v 假设任意边界值，这意味着 {\displaystyle u}u 必须满足边界条件
{\displaystyle {\frac {\partial u}{\partial n}}+\sigma u+g=0,}{\displaystyle {\frac {\partial u}{\partial n}}+\sigma u+g =0,}
在 {\displaystyle C.}{\displaystyle C.} 这个边界条件是 {\displaystyle u}u 的最小化属性的结果：它不是事先强加的。这样的条件称为自然边界条件。
如果 {\displaystyle \sigma }\sigma 在 {\displaystyle C.}{\displaystyle C} 上同样消失，则上述推理无效。在这种情况下，我们可以允许试函数 {\displaystyle \varphi \equiv c }{\displaystyle \varphi \equiv c,} 其中 {\displaystyle c}c 是一个常数。对于这样的试用功能，

{\displaystyle V[c]=c\left[\iint _{D}f,dx,dy+\int _{C}g,ds\right].}{\displaystyle V[c]=c\左[\iint _{D}f,dx,dy+\int _{C}g,ds\right].}
By appropriate choice of {\displaystyle c,}c, {\displaystyle V}V can assume any value unless the quantity inside the brackets vanishes.因此，变分问题是没有意义的，除非
{\displaystyle \iint _{D}f,dx,dy+\int _{C}g,ds=0.}{\displaystyle \iint _{D}f,dx,dy+\int _{ C}g,ds=0.}
这种情况意味着系统上的净外力处于平衡状态。如果这些力处于平衡状态，则变分问题有解，但它不是唯一的，因为可以添加任意常数。更多细节和例子在 Courant 和 Hilbert (1953) 中。

12. 特征值问题

一维和多维特征值问题都可以表述为变分问题。

Sturm-Liouville 问题
参见：Sturm-Liouville 理论
Sturm-Liouville 特征值问题涉及一般二次形式

{\displaystyle Q[\varphi ]=\int {x{1}}^{x_{2}}\left[p(x)\varphi ‘(x)^{2}+q(x)\varphi ( x)^{2}\right],dx,}{\displaystyle Q[\varphi ]=\int {x{1}}^{x_{2}}\left[p(x)\varphi ‘( x)^{2}+q(x)\varphi (x)^{2}\right],dx,}
其中 {\displaystyle \varphi }\varphi 仅限于满足边界条件的函数
{\displaystyle \varphi (x_{1})=0,\quad \varphi (x_{2})=0.}{\displaystyle \varphi (x_{1})=0,\quad \varphi (x_{2 })=0.}
令 {\displaystyle R}R 为归一化积分
{\displaystyle R[\varphi ]=\int {x{1}}^{x_{2}}r(x)\varphi (x)^{2},dx.}{\displaystyle R[\varphi ]=\int {x{1}}^{x_{2}}r(x)\varphi (x)^{2},dx.}
函数 {\displaystyle p(x)}p(x) 和 {\displaystyle r(x)}r(x) 需要处处为正且远离零。主要的变分问题是最小化所有满足端点条件的 {\displaystyle \varphi }\varphi 的比率 {\displaystyle Q/R}{\displaystyle Q/R}。如下所示，最小化 {\displaystyle u}u 的欧拉-拉格朗日方程为
{\displaystyle -(pu’)’+qu-\lambda ru=0,}{\displaystyle -(pu’)'+qu-\lambda ru=0,}
其中 {\displaystyle \lambda }\lambda 是商
{\displaystyle \lambda ={\frac {Q[u]}{R[u]}}.}{\displaystyle \lambda ={\frac {Q[u]}{R[u]}}.}
可以证明（见 Gelfand 和 Fomin 1963）最小化 {\displaystyle u}u 有两个导数并且满足欧拉-拉格朗日方程。关联的 {\displaystyle \lambda }\lambda 将表示为 {\displaystyle \lambda {1}}\lambda {1}；它是该方程和边界条件的最低特征值。相关的最小化函数将表示为 {\displaystyle u{1}(x).}{\displaystyle u{1}(x)。} 这种特征值的变分表征导致了瑞利-里兹方法：选择一个近似的 {\ displaystyle u}u 作为基函数（例如三角函数）的线性组合，并在这些线性组合中进行有限维最小化。这种方法通常出奇地准确。
下一个最小的特征值和特征函数可以通过在附加约束下最小化 {\displaystyle Q}Q

{\displaystyle \int {x{1}}^{x_{2}}r(x)u_{1}(x)\varphi (x),dx=0.}{\displaystyle \int {x {1}}^{x_{2}}r(x)u_{1}(x)\varphi (x),dx=0.}
可以扩展此过程以获得问题的特征值和特征函数的完整序列。
变分问题也适用于更一般的边界条件。除了要求 {\displaystyle \varphi }\varphi 在端点处消失，我们可以不在端点处施加任何条件，并设置

{\displaystyle Q[\varphi ]=\int {x{1}}^{x_{2}}\left[p(x)\varphi ‘(x)^{2}+q(x)\varphi ( x)^{2}\right],dx+a_{1}\varphi (x_{1})^{2}+a_{2}\varphi (x_{2})^{2},}{\显示样式 Q[\varphi ]=\int {x{1}}^{x_{2}}\left[p(x)\varphi ‘(x)^{2}+q(x)\varphi (x) ^{2}\right],dx+a_{1}\varphi (x_{1})^{2}+a_{2}\varphi (x_{2})^{2},}
其中 {\displaystyle a_{1}}a_{1} 和 {\displaystyle a_{2}}a_{2} 是任意的。如果我们设置 {\displaystyle \varphi =u+\varepsilon v}{\displaystyle \varphi =u+\varepsilon v}，比率 {\displaystyle Q/R}{\displaystyle Q/R} 的第一个变化是
{\displaystyle V_{1}={\frac {2}{R[u]}}\left(\int {x{1}}^{x_{2}}\left[p(x)u’( x)v’(x)+q(x)u(x)v(x)-\lambda r(x)u(x)v(x)\right],dx+a_{1}u(x_{ 1})v(x_{1})+a_{2}u(x_{2})v(x_{2})\right),}{\displaystyle V_{1}={\frac {2}{R [u]}}\left(\int {x{1}}^{x_{2}}\left[p(x)u’(x)v’(x)+q(x)u(x) v(x)-\lambda r(x)u(x)v(x)\right],dx+a_{1}u(x_{1})v(x_{1})+a_{2}u (x_{2})v(x_{2})\right),}
其中 λ 由比值 {\displaystyle Q[u]/R[u]}{\displaystyle Q[u]/R[u]} 给出，如前所述。分部整合后，
{\displaystyle {\frac {R[u]}{2}}V_{1}=\int {x{1}}^{x_{2}}v(x)\left[-(pu’)’ +qu-\lambda ru\right],dx+v(x_{1})[-p(x_{1})u’(x_{1})+a_{1}u(x_{1})] +v(x_{2})[p(x_{2})u’(x_{2})+a_{2}u(x_{2})].}{\displaystyle {\frac {R[u] }{2}}V_{1}=\int {x{1}}^{x_{2}}v(x)\left[-(pu’)‘+qu-\lambda ru\right], dx+v(x_{1})[-p(x_{1})u’(x_{1})+a_{1}u(x_{1})]+v(x_{2})[p( x_{2})u’(x_{2})+a_{2}u(x_{2})].}
如果我们首先要求 {\displaystyle v}v 在端点处消失，第一个变体对于所有这样的 {\displaystyle v}v 将消失，仅当
{\displaystyle -(pu’)‘+qu-\lambda ru=0\quad {\hbox{for}}\quad x_{1}<x<x_{2}.}{\displaystyle -(pu’)’ +qu-\lambda ru=0\quad {\hbox{for}}\quad x_{1}<x<x_{2}.}
如果 {\displaystyle u}u 满足这个条件，那么对于任意 {\displaystyle v}v，第一个变化将消失，仅当
{\displaystyle -p(x_{1})u’(x_{1})+a_{1}u(x_{1})=0,\quad {\hbox{and}}\quad p(x_{2 })u’(x_{2})+a_{2}u(x_{2})=0.}{\displaystyle -p(x_{1})u’(x_{1})+a_{1} u(x_{1})=0,\quad {\hbox{and}}\quad p(x_{2})u’(x_{2})+a_{2}u(x_{2})=0 .}
后面的这些条件是这个问题的自然边界条件，因为它们不是为了最小化而强加于试验函数，而是最小化的结果。

多维特征值问题
高维特征值问题的定义与一维情况类似。例如，给定一个域 {\displaystyle D}D 在三个维度上具有边界 {\displaystyle B}B，我们可以定义

{\displaystyle Q[\varphi ]=\iiint _{D}p(X)\nabla \varphi \cdot \nabla \varphi +q(X)\varphi ^{2},dx,dy,dz+\ iint _{B}\sigma (S)\varphi ^{2},dS,}{\displaystyle Q[\varphi ]=\iiint _{D}p(X)\nabla \varphi \cdot \nabla \varphi +q(X)\varphi ^{2},dx,dy,dz+\iint _{B}\sigma (S)\varphi ^{2},dS,}
和
{\displaystyle R[\varphi ]=\iiint _{D}r(X)\varphi (X)^{2},dx,dy,dz.}{\displaystyle R[\varphi ]=\iiint _{D}r(X)\varphi (X)^{2},dx,dy,dz.}
令 {\displaystyle u}u 是使商 {\displaystyle Q[\varphi ]/R[\varphi ],}{\displaystyle Q[\varphi ]/R[\varphi ],} 最小化的函数，没有规定条件在边界 {\displaystyle B.}B. {\displaystyle u}u 满足的欧拉-拉格朗日方程为
{\displaystyle -\nabla \cdot (p(X)\nabla u)+q(x)u-\lambda r(x)u=0,}{\displaystyle -\nabla \cdot (p(X)\nabla u)+q(x)u-\lambda r(x)u=0,}
在哪里
{\displaystyle \lambda ={\frac {Q[u]}{R[u]}}.}{\displaystyle \lambda ={\frac {Q[u]}{R[u]}}.}
最小化 {\displaystyle u}u 也必须满足自然边界条件
{\displaystyle p(S){\frac {\partial u}{\partial n}}+\sigma (S)u=0,}{\displaystyle p(S){\frac {\partial u}{\partial n}}+\sigma (S)u=0,}
在边界 {\displaystyle B.}B.这个结果取决于椭圆偏微分方程的正则性理论；详见 Jost 和 Li-Jost (1998)。许多扩展，包括完备性结果、特征值的渐近性质和关于特征函数节点的结果都在 Courant 和 Hilbert (1953) 中。

13. 具体应用

光学
费马原理指出，光的路径（局部）最小化其端点之间的光学长度。如果选择 {\displaystyle x}x 坐标作为沿路径的参数，并且沿路径 {\displaystyle y=f(x)}y=f(x)，则光学长度由下式给出

{\displaystyle A[f]=\int {x{0}}^{x_{1}}n(x,f(x)){\sqrt {1+f’(x)^{2}}} dx,}{\displaystyle A[f]=\int {x{0}}^{x_{1}}n(x,f(x)){\sqrt {1+f’(x)^{2 }}}dx,}
其中折射率 {\displaystyle n(x,y)}n(x,y) 取决于材料。如果我们尝试 {\displaystyle f(x)=f_{0}(x)+\varepsilon f_{1}(x)}{\displaystyle f(x)=f_{0}(x)+\varepsilon f_{1 }(x)} 那么 {\displaystyle A}A 的第一个变体（{\displaystyle A}A 关于 ε 的导数）是
{\displaystyle \delta A[f_{0},f_{1}]=\int {x{0}}^{x_{1}}\left[{\frac {n(x,f_{0}) f_{0}‘(x)f_{1}’(x)}{\sqrt {1+f_{0}‘(x)^{2}}}}+n_{y}(x,f_{0} )f_{1}{\sqrt {1+f_{0}’(x)^{2}}}\right]dx.}{\displaystyle \delta A[f_{0},f_{1}]=\ int {x{0}}^{x_{1}}\left[{\frac {n(x,f_{0})f_{0}‘(x)f_{1}’(x)}{\ sqrt {1+f_{0}‘(x)^{2}}}}+n_{y}(x,f_{0})f_{1}{\sqrt {1+f_{0}’(x) ^{2}}}\right]dx.}
在括号内对第一项进行部分积分后，我们得到欧拉-拉格朗日方程

{\displaystyle -{\frac {d}{dx}}\left[{\frac {n(x,f_{0})f_{0}‘}{\sqrt {1+f_{0}’^{2 }}}}\right]+n_{y}(x,f_{0}){\sqrt {1+f_{0}‘(x)^{2}}}=0.}{\displaystyle -{\ frac {d}{dx}}\left[{\frac {n(x,f_{0})f_{0}’}{\sqrt {1+f_{0}‘^{2}}}}\right ]+n_{y}(x,f_{0}){\sqrt {1+f_{0}’(x)^{2}}}=0.}
光线可以通过积分这个方程来确定。这种形式主义在拉格朗日光学和哈密顿光学的背景下使用。

斯涅尔定律
当光进入或离开透镜时，折射率存在不连续性。让

{\displaystyle n(x,y)={\begin{cases}n_{(-)}&{\text{if}}\quad x<0,\n_{(+)}&{\text{if }}\quad x>0,\end{cases}}}{\displaystyle n(x,y)={\begin{cases}n_{(-)}&{\text{if}}\quad x<0 ,\n_{(+)}&{\text{if}}\quad x>0,\end{cases}}}
其中 {\displaystyle n_{(-)}}{\displaystyle n_{(-)}} 和 {\displaystyle n_{(+)}}{\displaystyle n_{(+)}} 是常数。那么欧拉-拉格朗日方程在 {\displaystyle x<0}x<0 或 {\displaystyle x>0,}{\displaystyle x>0,} 的区域和以前一样成立，实际上路径在那里是一条直线，因为折射率是恒定的。在 {\displaystyle x=0,}{\displaystyle x=0,} {\displaystyle f}f 必须是连续的，但 {\displaystyle f’}f’ 可能是不连续的。在单独区域中按部分积分并使用欧拉-拉格朗日方程后，第一个变化形式为
{\displaystyle \delta A[f_{0},f_{1}]=f_{1}(0)\left[n_{(-)}{\frac {f_{0}‘(0^{-}) }{\sqrt {1+f_{0}’(0^{-}){2}}}}-n_{(+)}{\frac {f_{0}‘(0^{+})} {\sqrt {1+f_{0}’(0^{+}){2}}}}\right].}{\displaystyle \delta A[f_{0},f_{1}]=f_{ 1}(0)\left[n_{(-)}{\frac {f_{0}‘(0^{-})}{\sqrt {1+f_{0}’(0^{-}) {2}}}}-n_{(+)}{\frac {f_{0}‘(0^{+})}{\sqrt {1+f_{0}’(0^{+}){ 2}}}}\右]。}
乘以 {\displaystyle n_{(-)}}{\displaystyle n_{(-)}} 的因子是入射光线与 {\displaystyle x}x 轴的角度的正弦值，乘以 {\displaystyle n_ {(+)}}{\displaystyle n_{(+)}} 是折射光线与 {\displaystyle x}x 轴的角度的正弦值。斯涅尔折射定律要求这些项相等。正如这个计算所表明的，斯涅尔定律等效于光程长度的第一次变化消失。

三个维度的费马原理
使用矢量表示法是方便的：让 {\displaystyle X=(x_{1},x_{2},x_{3}),}{\displaystyle X=(x_{1},x_{2},x_{ 3}),} 令 {\displaystyle t}t 为参数，令 {\displaystyle X(t)}X(t) 为曲线 {\displaystyle C,}{\displaystyle C,} {\displaystyle {\dot {X}}(t)}{\dot {X}}(t) 是它的切向量。曲线的光学长度由下式给出

{\displaystyle A[C]=\int {t{0}}^{t_{1}}n(X){\sqrt {{\dot {X}}\cdot {\dot {X}}}} ,dt.}{\displaystyle A[C]=\int {t{0}}^{t_{1}}n(X){\sqrt {{\dot {X}}\cdot {\dot { X}}}},dt.}
请注意，这个积分对于 {\displaystyle C.}{\displaystyle C.} 的参数表示的变化是不变的。最小化曲线的欧拉-拉格朗日方程具有对称形式

{\displaystyle {\frac {d}{dt}}P={\sqrt {{\dot {X}}\cdot {\dot {X}}}},\nabla n,}{\displaystyle {\frac {d}{dt}}P={\sqrt {{\dot {X}}\cdot {\dot {X}}}},\nabla n,}
在哪里
{\displaystyle P={\frac {n(X){\dot {X}}}{\sqrt {{\dot {X}}\cdot {\dot {X}}}}}.}{\displaystyle P ={\frac {n(X){\dot {X}}}{\sqrt {{\dot {X}}\cdot {\dot {X}}}}}。}
由定义可知 {\displaystyle P}P 满足

{\displaystyle P\cdot P=n(X)^{2}.}{\displaystyle P\cdot P=n(X)^{2}.}
因此，积分也可以写成

{\displaystyle A[C]=\int {t{0}}^{t_{1}}P\cdot {\dot {X}},dt.}{\displaystyle A[C]=\int _ {t_{0}}^{t_{1}}P\cdot {\dot {X}},dt.}
这种形式表明，如果我们可以找到一个函数 {\displaystyle \psi }\psi，其梯度由 {\displaystyle P,}P 给出，那么积分 {\displaystyle A}A 由 {\displaystyle \ psi }\psi 在积分区间的端点。因此，研究使积分平稳的曲线问题可以与研究 {\displaystyle \psi .}\psi 的水平面有关。为了找到这样的函数，我们求助于波动方程，它支配光的传播。这种形式主义在拉格朗日光学和哈密顿光学的背景下使用。

与波动方程的联系
非均匀介质的波动方程为

{\displaystyle u_{tt}=c^{2}\nabla \cdot \nabla u,}{\displaystyle u_{tt}=c^{2}\nabla \cdot \nabla u,}
其中 {\displaystyle c}c 是速度，通常取决于 {\displaystyle X.}X。光的波前是这个偏微分方程的特征表面：它们满足
{\displaystyle \varphi _{t}^{2}=c(X){2},\nabla \varphi \cdot \nabla \varphi .}{\displaystyle \varphi _{t}^{2}= c(X)^{2},\nabla \varphi \cdot \nabla \varphi .}
我们可能会在表格中寻找解决方案

{\displaystyle \varphi (t,X)=t-\psi (X).}{\displaystyle \varphi (t,X)=t-\psi (X).}
在这种情况下，{\displaystyle \psi }\psi 满足

{\displaystyle \nabla \psi \cdot \nabla \psi =n^{2},}{\displaystyle \nabla \psi \cdot \nabla \psi =n^{2},}
其中 {\displaystyle n=1/c.}n=1/c。根据一阶偏微分方程理论，如果 {\displaystyle P=\nabla \psi ,}{\displaystyle P=\nabla \psi ,} 那么 {\displaystyle P}P 满足
{\displaystyle {\frac {dP}{ds}}=n,\nabla n,}{\displaystyle {\frac {dP}{ds}}=n,\nabla n,}
沿着由下式给出的曲线系统（光线）
{\displaystyle {\frac {dX}{ds}}=P.}{\displaystyle {\frac {dX}{ds}}=P.}
如果我们进行识别，这些用于求解一阶偏微分方程的方程与欧拉-拉格朗日方程相同

{\displaystyle {\frac {ds}{dt}}={\frac {\sqrt {{\dot {X}}\cdot {\dot {X}}}}{n}}.}{\displaystyle {\ frac {ds}{dt}}={\frac {\sqrt {{\dot {X}}\cdot {\dot {X}}}}{n}}。}
我们得出结论，函数 {\displaystyle \psi }\psi 是作为上端点函数的最小化积分 {\displaystyle A}A 的值。即，当构建最小化曲线族时，光程的值满足与波动方程对应的特征方程。因此，求解相关的一阶偏微分方程等效于找到变分问题的解族。这是汉密尔顿-雅可比理论的基本内容，适用于更一般的变分问题。

力学

在经典力学中，作用 {\displaystyle S,}S 被定义为拉格朗日函数 {\displaystyle L.}L 的时间积分。拉格朗日是能量的差异，

{\displaystyle L=T-U,}{\displaystyle L=T-U,}
其中 {\displaystyle T}T 是机械系统的动能，{\displaystyle U}U 是其势能。汉密尔顿原理（或作用原理）指出，保守的完整（可积约束）机械系统的运动使得作用积分
{\displaystyle S=\int {t{0}}^{t_{1}}L(x,{\dot {x}},t),dt}{\displaystyle S=\int {t{ 0}}^{t_{1}}L(x,{\dot {x}},t),dt}
对于路径 {\displaystyle x(t).}{\displaystyle x(t).} 的变化是静止的。该系统的欧拉-拉格朗日方程称为拉格朗日方程：
{\displaystyle {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {x}}}}={\frac {\partial L}{\partial x}},} {\displaystyle {\frac {d}{dt}}{\frac {\partial L}{\partial {\dot {x}}}}={\frac {\partial L}{\partial x}},}
它们等效于牛顿运动方程（对于此类系统）。
共轭动量 {\displaystyle P}P 定义为

{\displaystyle p={\frac {\partial L}{\partial {\dot {x}}}}.}{\displaystyle p={\frac {\partial L}{\partial {\dot {x}} }}。}
例如，如果
{\displaystyle T={\frac {1}{2}}m{\dot {x}}^{2},}{\displaystyle T={\frac {1}{2}}m{\dot {x }}^{2},}
然后
{\displaystyle p=m{\dot {x}}.}{\displaystyle p=m{\dot {x}}.}
如果通过拉格朗日 {\displaystyle L}L 到哈密顿量 {\displaystyle H 的勒让德变换引入共轭动量代替 {\displaystyle {\dot {x}}}{\dot {x}} }H 定义为
{\displaystyle H(x,p,t)=p,{\dot {x}}-L(x,{\dot {x}},t).}{\displaystyle H(x,p,t) =p,{\dot {x}}-L(x,{\dot {x}},t)。}
哈密​​顿量是系统的总能量： {\displaystyle H=T+U.}{\displaystyle H=T+U.} 与费马原理的类比表明，拉格朗日方程的解（粒子轨迹）可以用以下术语来描述{\displaystyle X.}X 的某个函数的水平面。该函数是 Hamilton-Jacobi 方程的解：
{\displaystyle {\frac {\partial \psi }{\partial t}}+H\left(x,{\frac {\partial \psi }{\partial x}},t\right)=0.}{ \displaystyle {\frac {\partial \psi }{\partial t}}+H\left(x,{\frac {\partial \psi }{\partial x}},t\right)=0.}

14. 极小值的变分和充分条件（Variations and sufficient condition for a minimum）

变分法关注泛函的变分，这是由于作为其参数的函数的微小变化而导致的泛函值的微小变化。一阶变分（first variation）被定义为泛函变化的线性部分，二阶变分（second variation）被定义为二次部分。

例如，如果 $J[y]$ 是一个以函数 $y=y(x)$ 作为参数的泛函，并且它的参数从 $y$ 到 $y+h$ 有一个小的变化，其中 $h=h(x)$ 是与 $y$ 处于同一函数空间的函数，则泛函的对应变化为：

$$\Delta J[h]=J[y+h]-J[y]$$

泛函 $J[y]$ 被认为是可微的，如果：

$$\Delta J[h]=\phi [h]+\epsilon \Vert h\Vert$$

其中 $\phi [h]$ 是线性泛函，$\Vert h\Vert$ 是 $h$ 的范数， 当 $\Vert h\Vert \to 0$，$\epsilon \to 0$。线性泛函 $\phi [h]$ 是 $J[y]$ 的一阶变分，并表示为：

$$\delta J[h]=\phi [h]$$

泛函 $J[y]$ 被称为是二次可微的，如果：

$$\Delta J[h]={\phi }_1[h]+{\phi }_2[h]+\epsilon \Vert h{\Vert }^2$$

其中 ${\phi }_1[h]$ 是线性泛函（一阶变分），${\phi }_2[h]$ 是二次泛函，随着 $\Vert h\Vert \to 0$，$\epsilon \to 0$。${\phi }_2[h]$ 是 $J[y]$ 的二次泛函，并表示为：

$${\delta }^{2}J[h]={\phi }_2[h]$$

二阶变分 ${\delta }^{2}J[h]$ 被认为是恒正的（stongly positive），如果对于所有 $h$ 和一些常数 $k>0$：

$${\delta }^{2}J[h]\ge k\Vert h{\Vert }^2$$

使用上面的定义，特别是一阶变分、二阶变分和恒正的定义，可以陈述以下最小泛函的充分条件。

极小值的充分条件：

如果在 $y=\hat{y}$，一阶变分 $\delta J[h]=0$，在 $y=\hat{y}$ ，二阶变分 ${\delta }^{2}J[h]$ 恒正，则泛函 $J[y]$ 在 $y=\hat{y}$ 有一个极小值。

15. 变分法的基本引理（Fundamental lemma of calculus of variations）

在数学中，特别是在变分法中，函数 $f$ 的变分 $\delta f$ 可以集中在任意小的区间上，但不能集中在单个点上。因此，极值的必要条件（函数导数为零）出现在与任意函数 $\delta f$ 集成的弱公式（weak formulation）（变分形式）中。变分法的基本引理（fundamental lemma of calculus of variations）通常用于将这个弱公式转换为强公式（微分方程），而无需与任意函数进行积分。证明通常利用这种可能性去选择 $\delta f$，$\delta f$ 集中在可以使 $f$ 保持符号（正或负）的区间上。引理的有几个版本。最基本的版本易于表示和证明。

15.1 基本形式

如果开区间 $(a,b)$ 上的连续函数 $f$ 对于 $(a,b)$ 上的所有紧致支持（compactly supported smooth functions）的平滑函数 $h$，满足等式：

$${\int }_a^{b}f(x)h(x)\mathrm{d}x=0$$

则 $f$ 为零。

这里的“平滑”可以解释为“无限可微”，但通常被解释为“两次连续可微”或“连续可微”，甚至只是“连续”，因为这些较弱的陈述对于给定的任务已经足够了。 “紧支持（compactly supported）”是指“对于某些 $c$，$d$ 使得 $a<c<d<b$"；但通常一个较弱的陈述就足够了，假设只有 $h$（或 $h$ 及其许多衍生物）在端点 $a$，$b$；在这种情况下使用闭区间 $[a,b]$。

15.2 两个给定函数的形式

如果区间 $(a,b)$ 上的一对连续函数 $f$，$g$ 对于 $(a,b)$ 上的所有紧支持的平滑函数 $h$，满足等式：

$${\int }_a^b(f(x)h(x)+g(x)h^{\prime }(x))\mathrm{d}x=0$$

则 $g$ 是可微的，并且处处 $g^{\prime }=f$。

$g=0$ 时的特殊情况只是基本形式。

另外当 $f=0$ 时的特殊情况（通常足够）：对于 (a,b) 上的所有平滑函数 $h$ 满足 $h(a)=h(b)=0$，如果区间 $(a,b)$ 上的连续函数 $g$ 满足等式：

$${\int }_a^{b}g(x)h^{\prime }(x)\mathrm{d}x=0$$

则 $g$ 是常数。

此外，如果假设 $g$ 连续可微，那么分部积分法将两个表述都简化为基本形式；这个例子由 Joseph-Louis Lagrange 给出，而 $g$ 的可微性证明由 Paul du Bois-Reymond 给出。

15.3 不连续函数的形式

给定的函数 $(f,g)$ 可以是不连续的，只要它们是局部可积的（在给定的区间上）。在这种情况下，Lebesgue 积分意味着，结论几乎无处不在（因此，在所有连续性点），$g$ 的可微性被解释为局部绝对连续性（而不是连续可微性）。有时给定的函数被假定为分段连续的，在这种情况下，黎曼积分就足够了，除了有限的不连续点集外，所有地方都说明了结论。

15.4 高阶导数下的形式

如果一个连续函数元组 $f_0,f_1,\cdots ,f_n$ 对于 $(a,b)$ 上所有紧支持的平滑函数 $h$，在区间 $(a,b)$ 上满足等式：

$${\int }_a^b(f_0(x)h(x)+f_1(x)h^{\prime }(x)+\cdots +f_n(x)h^{(n)}(x))\mathrm{d}x=0$$

则存在连续可微函数 $u_0,u_1,\dots ,u_{n-1}$，在 $(a,b)$ 上使得：

$$\begin{array}{rl}{f}_0& =u_0^{\prime },\\ f_1& =u_0+u_1^{\prime },\\ f_2& =u_1+u_2^{\prime }\\ ⋮& \\ f_{n-1}& =u_{n-2}+u_{n-1}^{\prime },\\ f_n& =u_{n-1}\end{array}$$

这个必要条件也是充分的，因为被积函数变为：

$$(u_{0}h{)}^{\prime }+(u_1{h}^{\prime }{)}^{\prime }+\cdots +(u_{n-1}{h}^{(n-1)}{)}^{\prime }$$

$n=1$ 的情况只是两个给定函数的版本，因为 $f=f_0=u_0^{\prime }$ 和 $f_1=u_0$，因此，$f_0-f_1^{\prime }=0$。

相反，$n=2$ 的情况不会导致关系 $f_0-f_1^{\prime }+f_2^{\prime \prime }=0$，因为函数 $f_2=u_1$ 不需要可微分两次。充分条件 $f_0-f_1^{\prime }+f_2^{\prime \prime }=0$ 是不必要的。相反，对于 $n=2$ 充分必要条件可以写成 $f_0-(f_1-f_2^{\prime }{)}^{\prime }=0$，对于 $n=3$，$f_0-(f_1-(f_2-f_3^{\prime }{)}^{\prime }{)}^{\prime }=0$，以此类推；通常，由于不可微分，括号不能打开。

15.5 向量值函数（Vector-valued functions）

推广到向量值函数 $(a,b)\to {\mathbb{R}}^d$ 很简单；将标量函数的结果分别应用于每个坐标，或从头开始处理向量值情况。

15.6 多变量函数（Multivariable functions）

如果开集 $\Omega \subset {\mathbb{R}}^d$ 上的连续多变量函数 $f$ 对于 $\Omega$ 上的所有紧支持的平滑函数 $h$，满足等式：

$${\int }_{\Omega }f(x)h(x)\mathrm{d}x=0$$

则 $f$ 完全为零。

与基本形式类似，可以考虑 $\Omega$ 闭包上的连续函数 $f$，假设 $h$ 在 $\Omega$ 的边界上消失（而不是紧支持）。

下面是不连续多变量函数的形式。

令 $\Omega \subset {\mathbb{R}}^d$ 为开集，且 $f\in L^2(\Omega )$ ，对于 $\Omega$ 上的所有紧支持的平滑函数 $h$，满足等式：

$${\int }_{\Omega }f(x)h(x)\mathrm{d}x=0$$

然后 $f=0$（在 $L^2$ 中，即几乎所有地方(almost everywhere)）。

15.7 紧致支持（Compact support）

• 紧致空间（Compact space）

在数学中，特别是一般拓扑学中，紧致性（compactness）是一种属性，旨在通过精确定义没有“洞”或“缺失端点”的空间的概念来概括欧几里得空间的封闭和有界子集的概念，即该空间不排除点的任何“极限值（limiting values）”。例如，“未闭合”区间 $(0,1)$ 不会是紧致的，因为它排除了 $0$ 和 $1$ 的“极限值”，而闭合区间 $[0,1]$ 将是紧致的。类似地，有理数（rational numbers）空间 $\mathbb{Q}$ 不是紧致的，因为它有无数个对应于无理数的“洞”，而实数空间 $\mathbb{R}$ 也不是紧致的，因为它排除了极限值 $\infty$ 和 $-\infty$。然而，扩展实数线（extended real number line）将是紧致的，因为它包含两个无穷大。有很多方法可以使这个启发式概念变得精确。这些方式在欧几里得空间中通常是一致的，但在其他拓扑空间中可能不等价。

图 根据 Heine-Borel 定理中所述的欧几里得空间的紧致性标准，区间 A = (-∞, -2] 不是紧致的，因为它是无界的。区间 C = (2, 4) 不是紧致的，因为它不是封闭的。区间 B = [0, 1] 是紧的，因为它既是封闭的又是有界的。

一个这样的概括是，如果从空间中采样的每个无穷点序列都有一个无穷子序列收敛到空间的某个点，则拓扑空间是顺序紧凑的（sequentially compact ）。（Bolzano-Weierstrass 定理）指出，欧几里得空间的一个子集在这种顺序意义上是紧致的当且仅当它是封闭的和有界的。因此，如果在闭单位区间 $[0,1]$ 中选择无限数量的点，则其中一些点将任意接近该空间中的某个实数。例如，序列 $1/2,4/5,1/3,5/6,1/4,6/7,\cdots$ 中的一些数字累积为 $0$（而其他数字累积为 $1$）。同一组点不会累加到开单位区间 (0, 1) 的任何一点上，因此开单位区间不是紧致的。尽管欧几里得空间的子集（子空间）可以是紧致的，但整个空间本身并不紧致，因为它是无界的。例如，考虑 ${\mathbb{R}}^1$，即整个实数线，点的序列 $0,1,2,3,\cdots$ , 没有收敛到任何实数的子序列。

紧致性由 Maurice Fréchet 于 1906 年正式引入，以将 Bolzano-Weierstrass 定理从几何点空间推广到函数空间。 Arzelà-Ascoli 定理和 Peano 存在定理举例说明了这种紧致性概念在经典分析中的应用。在最初的介绍之后，在一般度量空间中开发了各种等价的紧致性概念，包括顺序紧致性和极限点紧致性。然而，在一般拓扑空间中，这些紧致性概念不一定是等价的。非限定项（unqualified term）紧致性的最有用的概念和标准定义是这样表述的：“覆盖”空间的开集有限族（finite families of open sets）的存在，即空间的每个点都位于该开集所包含的某个集合中。这个更微妙的概念由 Pavel Alexandrov 和 Pavel Urysohn 在 1929 年提出，将紧空间展示为有限集的推广（generalizations of finite sets）。在这种意义上的紧致空间中，通常可以将局部存在的信息（即每个点的邻域）拼凑成在整个空间中存在的相应陈述，许多定理都具有这种性质。

在这种意义上紧凑的空间中，通常有可能将局部的信息，即在每个点的邻域内的信息，拼凑成对应的陈述（statements），这些陈述贯穿整个空间，许多定理都具有这种性质。

术语“紧致集（compact set）”有时用作紧致空间的同义词，但通常也指拓扑空间的紧致子空间（compact subspace）。

• 支持（Support）

在数学中，实值函数 $f$ 的支持（support）是包含未映射到零的元素的域的子集。 如果 $f$ 的域是拓扑空间，则 $f$ 的支持被定义为包含所有未映射到零的点的最小闭集。这个概念在数学分析中被广泛使用。

假设 $f:X\to \mathbb{R}$ 是一个实值函数，其定义域是任意集合 $X$。$f$ 的集合论支持（set-theoretic support），表示为 $\mathrm{supp}(f)$，其是 $X$ 中点的几何，其中对应的 $f$ 不为零：

supp ⁡ ( f ) = { x ∈ X   :   f ( x ) ≠ 0 } \operatorname {supp} (f)=\{x\in X\,:\,f(x)\neq 0\} supp(f)={x∈X:f(x)=0}

$f$ 的支持是 $X$ 的最小子集，其性质是 $f$ 在子集的补集上为零。如果对于所有有限的点 $x\in X$，$f(x)=0$，那么就说 $f$ 有有限的支持（finite support）。

如果集合 $X$ 有一个额外的结构（例如，一个拓扑），那么 $f$ 的支持被定义为类似于一个适当类型的 $X$ 的最小子集，使得 $f$ 在其补集上以适当的意义消失。支持的概念也以一种自然的方式扩展到比 $\mathbb{R}$ 更一般的集合中的取值函数和其他对象，例如测度（measures）或分布（distributions）。

• 闭支持（Closed support）

最常见的情况发生在 $X$ 是拓扑空间（例如实线或 $n$ 维欧几里得空间）且 $f:X\to \mathbb{R}$ 是一个连续实（或复）值函数。在这种情况下，$f$ 的支持（support）在拓扑上被定义为 $X$ 的子集的闭包（closure，在拓扑学中，拓扑空间中点的子集 $S$ 的闭包由 $S$ 中的所有点以及S的所有极限点组成。$S$ 的闭包可以等价地定义为 $S$ 及其边界的并集，也可以定义为包含 $S$ 的所有闭集的交集。直观地说，闭包可以被认为是在 $S$ 中或“附近” $S$ 中的所有点. 在S的闭包中的点是 $S$ 的闭包点。）（取于 $X$），其中 $f$ 不为零，即：

supp ⁡ ( f ) : = cl ⁡ X ( { x ∈ X   :   f ( x ) ≠ 0 } ) = f − 1 ( { 0 } c ) ‾ \operatorname {supp} (f):=\operatorname {cl} _{X}\left(\{x\in X\,:\,f(x)\neq 0\}\right)={ \overline {f^{-1}\left(\{0\}^{c}\right)}} supp(f):=clX​({x∈X:f(x)=0})=f−1({0}c)​

由于闭集的交集是闭集，$\mathrm{supp}(f)$ 是所有包含 $f$ 集合论支持（set-theoretic）的封闭集的交集。

例如，如果函数 $f:\mathbb{R}\to \mathbb{R}$ 被定义为：

$$f(x)=\{\begin{array}{ll}1-x^2& \text{if }|x|<1\\ 0& \text{if }|x|\ge 1\end{array}$$

那么 $f$ 的支持是闭区间 $[-1,1]$，因为 $f$ 在开区间 $(-1,1)$ 非零，而这个集合的闭包是 $[-1,1]$。

闭支持的概念通常应用于连续函数，但该定义对拓扑空间上的任意实数或复值函数有意义，并且一些作者不要求 $f:X\to \mathbb{R}$ 或 $f:X\to \mathbb{C}$ 是连续的。

• 紧支持（Compact support）

在拓扑空间 $X$ 上具有紧支持的函数是那些闭支持是 $X$ 的紧致子集的函数。如果 $X$ 是实线，或者 $n$ 维欧几里得空间，那么一个函数具有紧支持当且仅当它具有有界支持（bounded support），因为 ${\mathbb{R}}^n$ 的子集是紧的当且仅当它是闭和有界的。

例如，上面定义的函数 $f:\mathbb{R}\to \mathbb{R}$ 是一个紧致支持 $[-1,1]$ 的连续函数。如果 $f:{\mathbb{R}}^n\to \mathbb{R}$ 是一个平滑函数，因为 $f$ 在开子集 ${\mathbb{R}}^n\setminus \mathrm{supp}(f)$ 与 $0$ 相同，$f$ 的所有阶的偏导数在 ${\mathbb{R}}^n\setminus \mathrm{supp}(f)$ 上也是与 $0$ 完全相同的。

紧支持的条件比在无穷远处消失的条件强。例如，函数 $f:\mathbb{R}\to \mathbb{R}$ 定义为

$$f(x)=\frac{1}{1+x^2}$$

在无穷远处消失，因为随着 $|x|\to \infty$，$f(x)\to 0$，但它的支持 $\mathbb{R}$ 不是紧致的。

欧几里得空间上的实值紧支持（Real-valued compactly supported）平滑函数称为凹凸函数。Mollifiers 是凹凸函数（bump functions）的一个重要特例，因为它们可用于分布理论，通过卷积创建近似非平滑（广义）函数的平滑函数序列。

在好的情况下，具有紧支持的函数在无穷远处消失的函数空间中是密集的（dense），但是这个属性需要一些技术工作来证明给定示例的合理性。作为对更复杂示例的直觉，在极限语言中，对于任何 $\epsilon >0$，任何函数 $f$ 在实线上 $\mathbb{R}$，可以通过选择 $\mathbb{R}$ 的适当紧子集 $C$ 来近似，使得

$$\left|f(x)-I_C(x)f(x)\right|<\epsilon$$

对于所有 $x\in X$，其中 $I_C$ 是 $C$ 的指示函数（Indicator function）。紧致拓扑空间上的每个连续函数都有紧支持，因为紧致空间的每个闭子集确实是紧致的。

16. 更多应用

• 悬链线形状的推导
• 牛顿最小阻力问题的解法
• brachistochrone 问题的解决方案
• tautochrone 问题的解决方案
• 等距问题的解决方案
• 计算测地线
• 寻找最小曲面并解决高原问题
• 最佳控制
• 分析力学，或牛顿运动定律的重新表述，最著名的是拉格朗日和哈密顿力学；
• 几何光学，尤其是拉格朗日和哈密顿光学；
• 变分法（量子力学），一种寻找最低能量本征态或基态以及一些激发态的近似值的方法；
• 变分贝叶斯方法，一组用于逼近贝叶斯推理和机器学习中出现的棘手积分的技术；
• 广义相对论中的变分方法，使用变分法解决爱因斯坦广义相对论中问题的一系列技术；
• 有限元法是求微分方程中边值问题数值解的变分方法；
• 总变差去噪，一种用于过滤高方差或噪声信号的图像处理方法。

几乎所有的物理和力学的基本规律都陈述为规定某一泛函的变分应该是 0 的“变分法原理”，由于这个原故变分法使许多重要的物理问题及技术问题得以解决。

17. 泛函分析（Functional analysis）简介

wiki: Functional analysis

---

• 参考资料：

【数学百科】变分是什么？它和微分有什么区别？

wiki: Calculus of variations

wiki: Euler–Lagrange equation

wiki: Fundamental lemma of calculus of variations

wiki:Compact space

wiki: Mollifier

wiki: Bump function

wiki: Characteristic function

wiki: Indicator function

Beltrami identity