数理统计中的区间估计

区间估计

用点估计$\hat\theta(X_1,X_2,\dots,X_n)$来估计总体的未知参数 $\theta$，一旦我们获得了样本观察值 $(x_1,x_2,\dots,x_n)$，将它代入$\hat\theta(X_1,X_2,\dots,X_n)$，即可得到$\theta$的一个估计值。这很直观，也很便于使用。但是，点估计值只提供了$\theta$的一个近似值，并没有反映这种近似的精确度。同时，由于$\theta$本身是未知的，我们也无从知道这种估计的误差大小。因此，我们希望估计出一个真实参数所在的范围，并希望知道这个范围以多大的概率包含参数真值，这就是参数的区间估计问题。

定义

设$\theta$为总体$\xi$的未知参数,$\xi_1,\xi_2,\dots,\xi_n$为$\xi$的一个子样，$T1(\xi_1,\xi_2,\dots,\xi_n),T2(\xi_1,\xi_2,\dots,\xi_n)$ 为两个统计量。对于任意给定的$\alpha(0<\alpha<1)$，若$T_1,T_2$满足

$$P\{T_1\leq\theta\leq T_2\}=1-\alpha$$ ——(4)
则称随机区间 $[T_1,T_2]$为 $\theta$的置信水平为 $1-\alpha$的区间估计， $\alpha$为显著性水平， $T_1,T_2$分别称为置信下限和置信上限.
注意：也称$T_2-T_1$为该区间估计的精度。
值得注意的是，置信区间 $(\hat\theta_1,\hat\theta_2)$是一个随机区间，对于给定的样本 $(X_1,X_2,\dots,X_n)$， 可能包含未知参数 $(\hat\theta_1,\hat\theta_2)$，也可能不包含 $\theta$。但（4）表明，在重复取样下，将得到许多不同的区间 $\hat\theta_1(x_1,x_2,\dots,x_n)、\hat\theta_2(x_1,x_2,\dots,x_n)$，根据贝努利大数定律，这些区间中大约有 $100(1-\alpha)%$ 的区间包含未知参数 $\theta$ 。
置信度表示区间估计的可靠度，置信度 $1-\alpha$越接近于1越好。区间长度则表示估计的范围，即估计的精度，区间长度越短越好。当然，置信度和区间长度是相互矛盾的。在实际问题中，我们总是在保证可靠度的前提下，尽可能地提高精度。因此区间估计的问题，就是在给定 $\alpha$值的情况下，利用样本 $(X_1,X_2,\dots,X_n)$去求两个估计量 $\hat\theta_1$和 $\hat\theta_2$ 的问题。

置信区间的含义

以$\alpha=0.01$为例，此时置信度为$99%$。假设反复抽取样本1000次，则得到1000个随机区间$[T_1,T_2]$，在这1000个区间中，包含值的大约有990个，而不包含$\theta$值的大约有10个。

构造区间估计的步骤

1.构造一个与$\theta$有关的函数

$$\left\{\begin{aligned} U不含其它未知参数\\ 已知U的分布 \end{aligned} \right.$$
2.对给定的 $\alpha(0 < \alpha < 1)$，求 $a,b$ 使得
$$P\{a\leq U\leq b\}=1-\alpha$$
3.解不等式 $a\leq U\leq b \Leftrightarrow T_1\leq\theta\leq T_2$,得到区间 $[T_1,T_2]$

正态总体均值与方差的区间估计

设$\xi～N(a,\sigma^2),\xi_1,\dots,\xi_n$为$\xi$的一子样

单个总体$\xi ～ N(a,\sigma^2)$的情形

$\sigma^2=\sigma^2_0$已知时，求$a$的区间估计

因为$\overline \xi$是$a$的最优无偏估计，因此在求$a$的区间估计时，自然从$\overline \xi$出发来构造一个适合的函数。因为

$$\xi～N(a,\sigma_0^2) \Rightarrow\overline\xi～N(a,{\sigma^2_0\over n})$$
令 $U={\overline\xi-a \over \sigma_0/\sqrt{n}}$，则 $U～N(0,1)$
对给定的 $\alpha(0<\alpha<1)$，求 $u_\alpha$，使得
$$P\{|U|\leq u_\alpha\}=1-\alpha——(*)$$
临界值 $u_\alpha$可由 $P\{U \leq u_\alpha\}=1-\frac{\alpha}{2}$，查 $N(0，1)$分布表得到
（*）式变为
$$P\{ |{\overline\xi-a\over \sigma/\sqrt{n}}|\leq u_\alpha\}=1-\alpha$$
亦是
$$P\{ \overline\xi-u_\alpha\frac{\sigma_0}{\sqrt{n}}\leq a \leq \overline\xi+u_\alpha\frac{\sigma_0}{\sqrt{n}}\}=1-\alpha$$
因此 $a$的置信水平为 $1-\alpha$的区间估计为
$$[\overline\xi-u_\alpha\frac{\sigma_0}{\sqrt{n}},\overline\xi+u_\alpha\frac{\sigma_0}{\sqrt{n}}]$$
不同置信水平 $1-\alpha$下， $a$的区间估计为

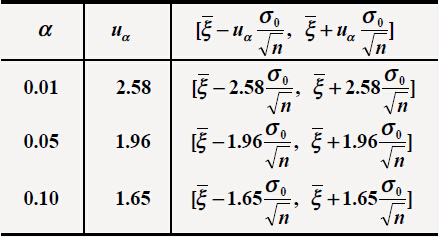
例题

设某种清漆的9个样品，其干燥时间(以小时计)分别为$6.0 ， 5.7 ， 5.8 ， 6.5 ， 7.0 ， 6.3 ，5.6 ，6.1 ，5.0$ ,
设干燥时间总体服从正态分布$N(a,0.6^2)$，求a的置信
水平为$0.95$的置信区间。
解：