熟悉决策树算法的人都知道ID3以及C4.5两种算法,当然也非常清楚信息增益以及信息增益率两个概念。
信息增益:节点M的信息熵E1与其全部子节点信息熵之和E2的差。
信息增益率:节点信息增益与节点分裂信息度量的比值。
信息增益是ID3算法的基础,信息增益率是C4.5算法的基础。同时,C4.5是ID3算法的改进版,改进了某些情况下,决策树构建过程中过拟合的问题。
首先说一下信息增益:
在网上,我们可以轻松找到信息增益的计算公式,乍一看,公式极为简单,只是两个熵减一下,但实际上,当我们去代码实现时,却可能会遇到,究竟该如何计算Entropy(S)跟Gain(S,A)的问题。
S是样本集合这句话描述的并不清晰,对于初学决策树模型的人来说,把S说成所有位于节点M的样本的集合,或许更为恰当。
之所以这么说,是因为下图
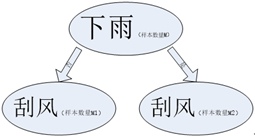
同样是刮风的属性,但是,样本的数量却发生的变化,这在决策树的构建过程中是经常遇到的现象。
属性会重复出现?有些人或许会感到不解,但是看weka使用J48跑测试样例的结果,大家或许就能明了了。
在一条从上往下的路径中,petalwidth属性出现了两次呢。
许多刚刚学习决策树的人很难理解为什么计算一个节点的时候需要用到样本(误以为是整个样本)集合,其实这里的样本集合指的是,当前在某个节点N上的样本集合SN;
使用数学话的形式表述信息增益前,定义几个常用的变量,使用变量表示节点A上的样本集合,使用
表示在节点A的全部样本中属于类别Ci的样本数量,使用NAm表示在节点A选择属性m的样本数量,用
表示选择属性m的样本中,属于类别Ci的样本数量。
这样我们可以表示出节点A的熵为,注意,这里直接使用了概率公式替换了前面公式中的p;
节点A的属性有M个,所以Gain(S,A)即可表述成如下形式
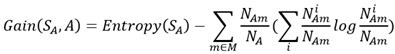
有了信息增益的实际表达式之后,我们再根据信息增益率的描述写出信息增益率的表达式:
信息增益比率实际在信息增益的基础上,又将其除以一个值,这个值一般被成为分裂信息量,是将属性可选值m作为划分,计算节点上样本总的信息熵。
大家可以在网上找到如下公式:
必须说,直接去写S很容易误导人,所以我将公式重写了一下,如下:
然后,我们将之前定义的变量代入到公式中,可以得到GainRatio(SA,A)的最终表达式:
即:
大家一定要注意,计算节点熵和计算节点分类信息量的时候,样本的划分标准一个是类别,一个是节点的可选属性!!
最后的公式可能有点复杂,但是如果一点一点拼凑起来的话,其实很简单,以此勉励。








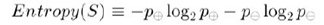
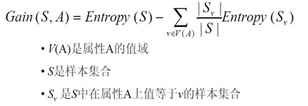

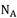
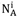
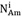
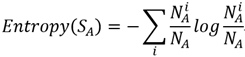
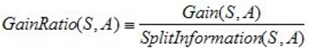
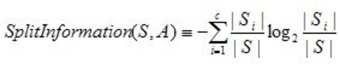
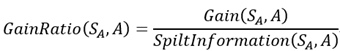
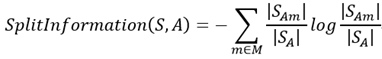
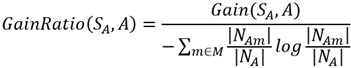
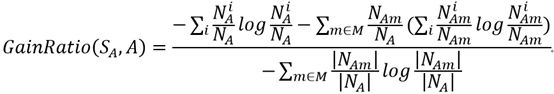
















 1503
1503

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








