优化问题

线性规划

优化目标和约束条件都是线性的优化问题，属于线性规划，其主要解法有：

1. 图解法
2. 单纯形法

整数规划

在线性规划问题的基础上，可能某些问题存在必须是整数的约束，那么这就转化为整数规划问题，主要解法有：

1. 分支定界法‘
2. 割平面法

非线性规划

优化目标或者约束条件存在非线性的优化问题，属于非线性规划，其主要分为无约束问题和有约束问题。下面介绍几个重要的概念：

凸函数和严格凸函数
形如$f(\alpha{x_1}+(1-\alpha)x_2)\leqslant \alpha{f(x_1)}+(1-\alpha)f(x_2)$则称之为凸函数，其中$0<\alpha<1$;

凸函数的极值
对于定义在凸集上的凸函数而言，其局部极值就是其全局极值。

无约束极值问题的求解方法

1. 梯度下降法，也就是搜索方法是负梯度方法，他是使得函数值下降最快的方向。最速下降法有锯齿现像，收敛速度慢；
2. 牛顿迭代法，牛顿法是二次收敛的，并且收敛阶数是2。一般目标函数在最优点附近呈现为二次函数，于是可以想像最优点附近用牛顿迭代法收敛是比较快的。而在开始搜索的几步，我们用梯度下降法收敛是比较快的。将两个方法融合起来可以达到满意的效果。收敛快是牛顿迭代法最大的优点，但也有致命的缺点：Hesse矩阵及其逆的求解计算量大
3. 拟牛顿法，Hesse矩阵在拟牛顿法中是不计算的，拟牛顿法是构造与Hesse矩阵相似的正定矩阵，这个构造方法，使用了目标函数的梯度（一阶导数）信息和两个点的“位移”$x_k-x_{k-1}$来实现。
4. 共轭方向法，最速下降法有锯齿现像，收敛速度慢；而牛顿法需要计算Hesse矩阵而计算量大。共轭方向法收敛速度界于两者之间，具有二次收敛性。共轭方向法属于效果好而又实用的方法。由于一般目标函数在最优点附近呈现为二次函数，因此可以设想一个算法对于二次函数比较有效，就可能对一般函数也有较好效果。共轭方向法是在研究对称正定二次函数的基础上提出来的。
5. 共轭梯度法，共轭梯度法是共轭方向法的一种延伸，初始共轭向量$P_0$由初始迭代点$x_0$处的负梯度$-g_0$来给出。以后的$P_k$由当前迭代点的负梯度与上一个共轭向量的线性组合来确定.

约束极值问题的求解方法
约束极值问题比无约束极值问题复杂得多。下面首先介绍几个重要的概念：
库恩-塔克（KT条件或者KKT条件）：
首先介绍一下优化问题：

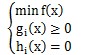
对于约束条件，$h_i$称之为起作用约束（有效约束），因为其处于作用域的边界，任何扰动都可以使得结果”崩溃”；$g_i$可以分为=和>两部分，其中=部分属于有效约束，而>属于无效约束或者不起作用约束。
假设$x_0$是极值点，$\triangledown g(x_0)$是$x_0$在有效约束下的梯度，$\triangledown f(x_0)$是$x_0$在目标函数下的梯度（这里补充一下，梯度对于标量函数而言对应增长最快的方向，那么负梯度便对应下降最快的方向）。则下列关系必然不存在：

$$\begin{matrix} -\triangledown f(x_0)*D > 0\\ \triangledown g(x_0)*D > 0 \end{matrix}$$
即不存在一个可行下降方向，那么就存在 $\triangledown f(x_0)=\lambda\triangledown g(x_0)$,其中 $\lambda<0$。

所以KKT条件就是约束条件和拉格朗日乘子等于0，即 $\alpha_ig(x)=0$，当 $\alpha_i=0$时，对应的样本不是支持向量，而支持向量对应的 $\alpha_i=0$.

顺便插一句，承接上一篇的SVM。 非线性SVM可用经典的二次规划方法求解，但同时求解n个拉格朗日乘子涉及很多次迭代，计算开销太大。所以一般采用Sequential Minimal Optimization(SMO)算法。其基本思路是每次只更新两个乘子，迭代获得最终解。计算流程可表示如下：

 For i=1:iter

    1.根据预先设定的规则，从所有样本中选出两个
    2.保持其它拉格朗日乘子不变，更新所选样本对应的拉格朗日乘子

 End

SMO算法的优点在于，只有两个变量的二次规划问题存在解析解。关键的技术细节在于，一是在每次迭代中，怎样更新乘子；二是怎样选择每次迭代需要更新的乘子。此外求解SVM另外一种方法是LS-SVM，与SVM的关键不同是约束条件由不等式变为了等式，对应的优化问题：

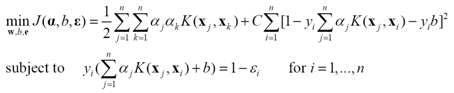
不等式变为等式后，拉格朗日乘子可以通过解线性系统得到：

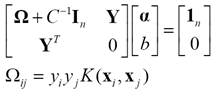
解线性系统远易于解二次规划问题。但相应地，绝大部分拉格朗日乘子都将不为零。也就是说，LS-SVM分类器的测试时间将长于SVM分类器。