凸多边形的极值点

最新推荐文章于 2023-05-28 22:28:35 发布

SimpleFelix

最新推荐文章于 2023-05-28 22:28:35 发布

阅读量1.4k

点赞数

分类专栏：计算几何算法与实现文章标签：几何学

本文链接：https://blog.csdn.net/u013279723/article/details/104458627

版权

计算几何算法与实现专栏收录该内容

10 篇文章 16 订阅

订阅专栏

前言

在计算几何中，我们经常需要寻找一个2D多边形（Polygon）的极值点。例如通过x\y的极值点，我们可以定义一个多边形的包围盒。更一般的情况下，我们可能会需要寻找一个多边形在任意方向上的极值点。对于n个点的点集，很容易找到一个O(n)的算法，只需要依次测试每个点即可。然而对于凸多边形，可以利用二分搜索的思想在 $O(log(n))$ 时间内找到极值点。首先，定义一个任意的方向向量u，接下来我们详细讲解该算法的思路。

平面点集和简单多边形的凸包在这两篇博文中已经介绍过了：平面点集的凸包算法、多边形快速凸包算法。因此，对于平面点集和任意简单多边形只需要先计算凸包，然后再计算凸包极值点即可。其算法复杂度由凸包算法决定。

凸包极值点算法

首先，定义2D凸多边形S由n个点构成V0,V1,...,Vn-1,Vn=V0，并且沿着逆时针方向给定。

定义 $e_i$ 为第i条边（从Vi到Vi+1）， $\mathbf{ev_i}=V_{i+1}-V_i$ 为边向量。

目标：找到S中的所有点在u方向上的极值点。也就是将点投影在u说定义的直线上，极值点就是投影点的极值点，如下图所示：

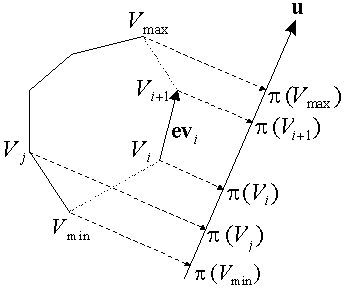
可以看到，相对于u，Vi在Vj之上。也就是（Vi-Vj）与u之间形成一个锐角，相当于下面的几何条件：

$\mathbf{u}*(V_i-V_j)>0$

这个条件可以帮助我们判断，一条边 $e_i$ 相对于u的投影是在增加还是减少。

暴力算法

最直接的办法就是暴力搜索每个点，每一步与当前保存的极值点比较。该算法的伪代码如下：

Input: W = {V0,V1,...,Vn-1}  n个点的点集
       u = 给定的方向向量
记 max = min = 0。
for each point Vi in {V1,...,Vn-1}  (i=1,n-1)
{
    if (u · (Vi - Vmax) > 0) {  // Viis above the prior max
        max = i;                // new max index = i
        continue;               // a new max can't be a new min
    }
    if (u · (Vi - Vmin) < 0)    // Vi is below the prior min
        min = i;                // new min index = i
}

return max = 最大值点的Index
       min = 最小值点的Index

尽管算法是线性的，但还可以通过二分搜索加快。

二分搜索

对于一个凸多边形的点集，我们可以通过二分搜索，在 $O(log(n))$ 时间内找到极值点。

首先，假设极大值点在顶点Va和Vb之间，Vc为Va和Vb的中间点，为了实现二分搜索，我们需要将下一步的搜索范围缩小到[a, c]或者[c, b]。由于多边形是凸的，我们可以通过比较A、C处的边向量 $\mathbf{ev}_a$ 、 $\mathbf{ev}_c$ 来做到这一点。下面详细说明：

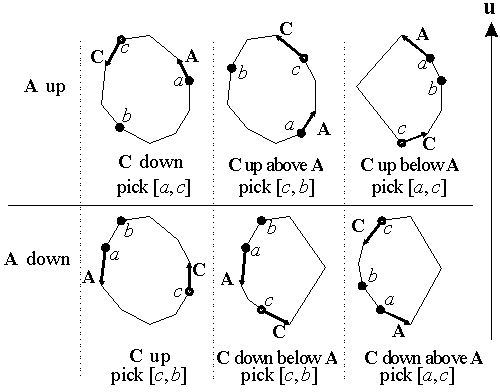
如上图所示。假定u向上，A、B、C的相对位置可能有6种情况。对于每种情况，要么[a, c]，要么[c, b]包含最大值点。这是因为，多边形S在u方向上是单调的，它由两个单调链组成，从最小值点开始，到最大值点单调递增，然后再单调递减回到最小值点。而且无论u的方向如何，这个结论都是成立的。

接下来，我们就能构造二分搜索了。从 $[a=0,b=n]$ 开始， $c=\left \lfloor (a+b)/2 \right \rfloor$ ,在每一步，我们需要确定是将a增加到c,还是b减小到c，将包含最大值的区间缩小一半。当然，我们需要检查，是否已经找到了一个局部极大值点Vc，这只需要检查 $\mathbf{ev}_{c-1}\cdot \mathbf{u}$ 和 $\mathbf{ev}_{c}\cdot \mathbf{u}$ 的符号是否一致即可。如果两者的符号不一致，说明Vc是局部极大值点，同时也是多边形的全局最大值点。

于是，我们得到，寻找相对于u的最大值点的伪代码如下：

Input: OMEGA = {V0,V1,...,Vn-1,Vn=V0} is a 2D proper convex polygon
       u = a 2D direction vector

if V0 is a local maximum, then return 0;
Put a=0; b=n;
Put A = the edge vector at V0;
forever {
    Put c = the midpoint of [a,b] = int((a+b)/2);
    if Vc is a local maximum, then it is the global maximum
        return c;

    // no max yet, so continue with the binary search
    // pick one of the two subchains [a,c] or [c,b]
    Put C = the edge vector at Vc;
    if (A points up) {
        if (C points down) {
            b = c;                     select [a,c]
        }
        else C points up {
            if Va is above Vc {
                 b = c;                 select [a,c]
            }
            else Va is below Vc {
                 a = c;                 select [c,b]
                 A = C;
            }
        }
    }
    else A points down {
        if (C points up) {
            a = c;                     select [c,b]
            A = C;
        }
        else C points down {
            if Va is below Vc {
                 b = c;                 select [a,c]
            }
            else Va is above Vc {
                 a = c;                 select [c,b]
                 A = C;
            }
        }
    }
    if (b <= a+1) then the chain is impossibly small
        return an error; since something's  wrong
}

下面是二分搜索算法的一个C++实现：

// Assume that classes are already given for the objects:
//    Point and Vector (2D) with:
//        coordinates {float x, y;}
//        operators for:
//            == to test equality
//            != to test inequality
//            =  for assignment
//            -Vector for unary minus
//            Point  = Point ± Vector
//            Vector = Point - Point
//            Vector = Vector ± Vector
//    Line with defining points {Point P0, P1;}
//===================================================================


// dot product (2D) which allows vector operations in arguments
#define dot(u,v)   ((u).x * (v).x + (u).y * (v).y)

// tests for vector orientation relative to a direction vector u
#define up(u,v)         (dot(u,v) > 0)
#define down(u,v)       (dot(u,v) < 0)
#define dr(u,Vi,Vj)     (dot(u, (Vi)-(Vj))) // direction sign of (Vi-Vj)
#define above(u,Vi,Vj)  (dr(u,Vi,Vj) > 0)   // true if Vi is above Vj
#define below(u,Vi,Vj)  (dr(u,Vi,Vj) < 0)   // true if Vi is below Vj
 

// polyMax_2D(): find a polygon's max vertex in a specified direction
//    Input:  U   = a 2D direction vector
//            V[] = array vertices of a proper convex polygon
//            n   = number of polygon vertices, with V[n]=V[0]
//    Return: index (>=0) of the maximum vertex, or
//            (-1) = an error [Note: should be impossible, but...]
int
polyMax_2D( Vector U, Point* V, int n )
{
    if (n < 10) {               // use brute force search for small polygons
        int max = 0;
        for (int i=1; i<n; i++)     // for each point in {V1,...,Vn-1}
            if (above(U, V[i], V[max]))  // if V[i] is above prior V[max]
                 max = i;                // new max index = i
        return max;
    }

    // use binary search for large polygons
    int     a, b, c;            // indices for edge chain endpoints
    Vector  A, C;               // edge vectors at V[a] and V[c]
    int     upA, upC;           // test for "up" direction of A and C

    a=0; b=n;                   // start chain = [0,n] with V[n]=V[0]
    A = V[1] - V[0];
    upA = up(U,A);
    // test if V[0] is a local maximum
    if (!upA && !above(U, V[n-1], V[0]))    //  V[0] is the maximum
        return 0;

    for(;;) {
        c = (a + b) / 2;        // midpoint of [a,b], and 0<c<n
        C = V[c+1] - V[c];
        upC = up(U,C);
        if (!upC && !above(U, V[c-1], V[c])) // V[c] is a local maximum
            return c;                        // thus it is the maximum

        // no max yet, so continue with the  binary search
        // pick one of the two subchains [a,c]  or [c,b]
        if (upA) {                       // A points up
            if (!upC) {                      // C points down
                 b = c;                       // select [a,c]
            }
            else {                           // C points up
                 if (above(U, V[a], V[c])) {    // V[a] above V[c]
                     b = c;                       // select [a,c]
                 }
                 else {                         // V[a] below V[c]
                     a = c;                       // select [c,b]
                     A = C;
                     upA = upC;
                 }
            }
        }
        else {                           // A points down
            if (upC) {                       // C points up
                 a = c;                       // select [c,b]
                 A = C;
                 upA = upC;
            }
            else {                           // C points down
                 if (below(U, V[a], V[c])) {    // V[a] below V[c]
                     b = c;                       // select [a,c]
                 }
                 else {                         // V[a] above V[c]
                     a = c;                       // select [c,b]
                     A = C;
                     upA = upC;
                 }
            }
        }
        // have a new (reduced) chain [a,b]
        if (b <= a+1)           // the chain is impossibly small
            return (-1);        // return an error: something's wrong
    }
}
//===================================================================

SimpleFelix

关注

0
点赞
踩
4

收藏

觉得还不错? 一键收藏
0
评论
凸多边形的极值点

前言在计算几何中，我们经常需要寻找一个2D多边形（Polygon）的极值点。例如通过x\y的极值点，我们可以定义一个多边形的包围盒。更一般的情况下，我们可能会需要寻找一个多边形在任意方向上的极值点。对于n个点的点集，很容易找到一个O(n)的算法，只需要依次测试每个点即可。然而对于凸多边形，可以利用二分搜索的思想在时间内找到极值点。首先，定义一个任意的方向向量u，接下来我们详细讲解该算法的思路。...
复制链接

扫一扫