指标重要性的量化方法 熵值法 Entropy Weight Method

01.定义    

    在上一篇文章中，我们介绍了层次分析法，但该方法存在一定的局限性：评价极具主观性。但是在实际数据评价分析中，我们需要更具客观的方法评价。

    本文介绍一种客观的赋权重的数据分析方法-熵值法。熵值法（Entropy Weight Method）是一种常用于多指标决策分析的方法，其计算原理基于信息熵理论。该方法可以将不同指标的重要性进行量化，并将其应用于多目标决策、评价和排名等领域。
    熵是信息论中的一个概念，用来描述一个随机事件的不确定性和信息量的大小。在熵值法中，熵值的计算公式是基于信息熵的，通过将指标的取值范围等分成若干等份，计算每个等份的概率，再将概率带入信息熵的公式进行计算得到指标的熵值。熵值是用来量化指标的波动和不确定性的指标。熵值越大，表示该指标的波动和不确定性越大，其对决策结果的影响也越大。多目标决策中，通过计算各个指标的熵值，可以对各个指标的重要性进行量化，进而确定各个指标的权重，使得决策更加科学、客观和准确。

02.计算原理

    熵值法的计算原理较为简单，主要分为四步。但在计算之前需要对原始数据进行预处理，在实际问题中，对于一个问题可能存在多个指标，而不同的指标可能会存在以下几种情况：①指标值越大越好；②指标值越小越好；③呈类似正态分布曲线，在中间某一个点时最好。

    对于不同种类情况的指标存在不同的数据预处理方法，但要明白的是，我们对于数据进行预处理的最初目的是为了消除不同指标之间的单位和量纲的影响。因此，通常我们选择将所有指标放缩到[0,1]区间之内进行分析。

    值得注意的是，此时如果直接选择归一化，会存在一个致命的问题，就是前面提到的不同指标数据存在的三种分散情况。我们在正式归一化前，需要将所有指标同向化（指标正同向化：即所有指标都是数值越大越好；指标负同向化：即所有指标都是数值越小越好）。在本文中，采用指标正同向化处理数据，即对原始数据按情况进行以下计算：

    设有m个待评对象，n个评价指标，可以构成数据矩阵：

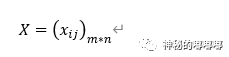
设数据矩阵内元素，经过指标正向化处理过后的元素为 ：

Step0：指标正同向化

    注意：指标正同向化方法不一定，大家也可以自行推导，只要不改变指标性质的基础即可。除此之外，要注意去负数化，即如果指标中存在负数，应该先将原始数据归一化至[0,1]区间内，再进行指标同向化。

    ①越小越好型指标：

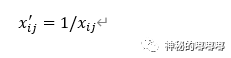
    ②越大越好型指标：

    ③正态分布曲线型：

Step1：归一化处理

    将所有指标正同向化后，再将其进行归一化处理，归一化后的矩阵为（Rij）m*n：

    这里的归一化，在以前的博文中有详细讲过，如果忘记了，可以看链接：

数据预处理之回归类模型

Step2：计算各指标的熵值

    这一步注意的是Pij不能为0，否则进行对数运算会报错，如果要解决这个情况，只需要再上一步归一化时，将区间下限设置稍微大于0即可。如果某个指标的信息熵   越小,就表明其指标值的变异程度越大，提供的信息量也越大，可以认为该指标在综合评价起到作用也越大。

Step3：计算指标的权重

Step4：求加权和，并得出结论

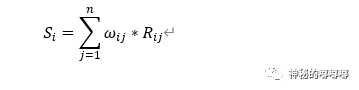
03.代码实现

    本文使用了经典购买轿车决策案例，原始数据如下所示：

	油耗	功率	价格	安全性	维护	操作
本田	5	1.4	6	3	5	7
奥迪	9	2	30	7	5	9
桑塔纳	8	1.8	11	5	7	5
别克	12	2.5	18	7	5	5

%% 计算代码如下所示：
%% 程序初始化
clear all
clc

%% 原始数据读取
data = [5,1.4,6,3,5,7;9,2,30,7,5,9;8,1.8,11,5,7,5;12,2.5,18,7,5,5];
[m,n] = size(data);

%% 指标正同向化
% 我们再这里认为油耗、费用、操作性越小越好；功率、安全性、维护性越高越好
% 越小越好型数据处理
index = [1,3,6];
for i =1:length(index)
    data(:,index(i)) = 1./data(:,index(i));
end

%% 数据归一化
% 由于mapminmax是按行归一化，所以归一化前先将其转置,且为了不出现0，所以将归一化范围下线设定为0.001
new_data = mapminmax(data',0.001,1);
new_data = new_data';

%% 计算个指标熵值
% Step1:求Pij
for i = 1:m
    for j = 1:n
        P(i,j) = new_data(i,j)/sum(new_data(:,j));
    end
end


% Step2:求Ej
for i = 1:m
    for j = 1:n
        e(i,j) = P(i,j)*log(P(i,j));
    end
end

for j=1:n
    E(j)=-1/log(m)*sum(e(:,j));
end

%% 差异系数
g = 1-E;

%% 计算指标权重
for j = 1:n
    w(j) = g(j)/sum(g);
end

disp('各指标权重为：')
disp(w)

%% 计算得分
for i =1:m
    score(i,1) = sum(new_data(i,:).*w);
end

disp('各品牌综合分数为：')
disp(score)

    熵值法虽然是根据各项指标指标值的变异程度来确定指标权数的，这是一种客观赋权法，避免了人为因素带来的偏差。但仍存在一定的缺点：忽略了指标本身重要程度，有时确定的指标权数会与预期的结果相差甚远，同时熵值法不能减少评价指标的维数。

原文：数据评价分析-熵值法