《统计学习方法》学习笔记（4）--k近邻法及常用的距离（or 相似度）度量

一、k近邻法基础知识
1. 特征空间中两个实例点的距离反应了两个实例点的相似程度。
2. k近邻模型三要素 = 距离度量（有不同的距离度量所确定的最邻近点不同）+k值的选择（应用中，k值一般取一个比较小的值，通常采用交叉验证法来确定最优k值）+分类决策规则（往往是多数表决规则（majority voting rule），此规则等价于经验风险最小化）
3. 在训练数据量太大或者是维数很高时，显然线性扫描（linear scan）耗时太大，不可取。其中一个办法就是构建kd树（空间划分树，实际上是一种平衡二叉树）实现对训练数据的快速k近邻搜索。
二、距离度量相关

Note：根据数据特性的不同，可以采用不同的度量方法。一般而言，定义一个距离函数 d(x,y), 需要满足下面几个准则：
1) d(x,x) = 0 // 到自己的距离为0
2) d(x,y) >= 0 // 距离非负
3) d(x,y) = d(y,x) // 对称性: 如果 A 到 B 距离是 a，那么 B 到 A 的距离也应该是 a
4) d(x,k)+ d(k,y) >= d(x,y) // 三角形法则: (两边之和大于第三边)

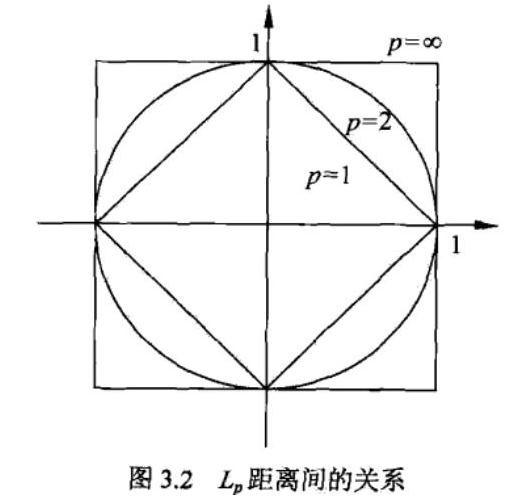
1. 闵可夫斯基距离(Minkowski Distance)又称Lp距离，闵氏距离不是一种距离，而是一组距离的定义。
   两个n维变量a(x11,x12,…,x1n)与 b(x21,x22,…,x2n)间的闵可夫斯基距离定义为：
   
   其中p是一个变参数，根据变参数的不同，闵氏距离可以表示一类的距离。
   当p=1时，就是曼哈顿距离，又称L1距离或者是程式区块距离（city block distance）等。
   当p=2时，就是欧氏距离，又称L2距离，是直线距离。
   当p→∞时，就是切比雪夫距离
   
   闵氏距离，包括曼哈顿距离、欧氏距离和切比雪夫距离都存在明显的缺点。
   　　举个例子：二维样本(身高,体重)，其中身高范围是150~190，体重范围是50~60，有三个样本࿱