在 3DTiles 的官方文档中详细介绍了关于几何度量误差 Geometric Error 的一些理念和内涵,概括来说可以翻译为如下定义:
几何度量误差,Geometric Error,简称 GE,是计算机图形图像学领域中用来描述计算机绘制的近似几何模型与理想数学模型之间近似程度的一种度量误差。
除此之外,与几何度量误差概念相似但表现形式不同的还有一个名为 Screen Space Error 的屏幕空间误差,是几何度量误差在三维渲染管线处理后最终呈现在屏幕上的一种表现形式。二者之间的关系如下图:
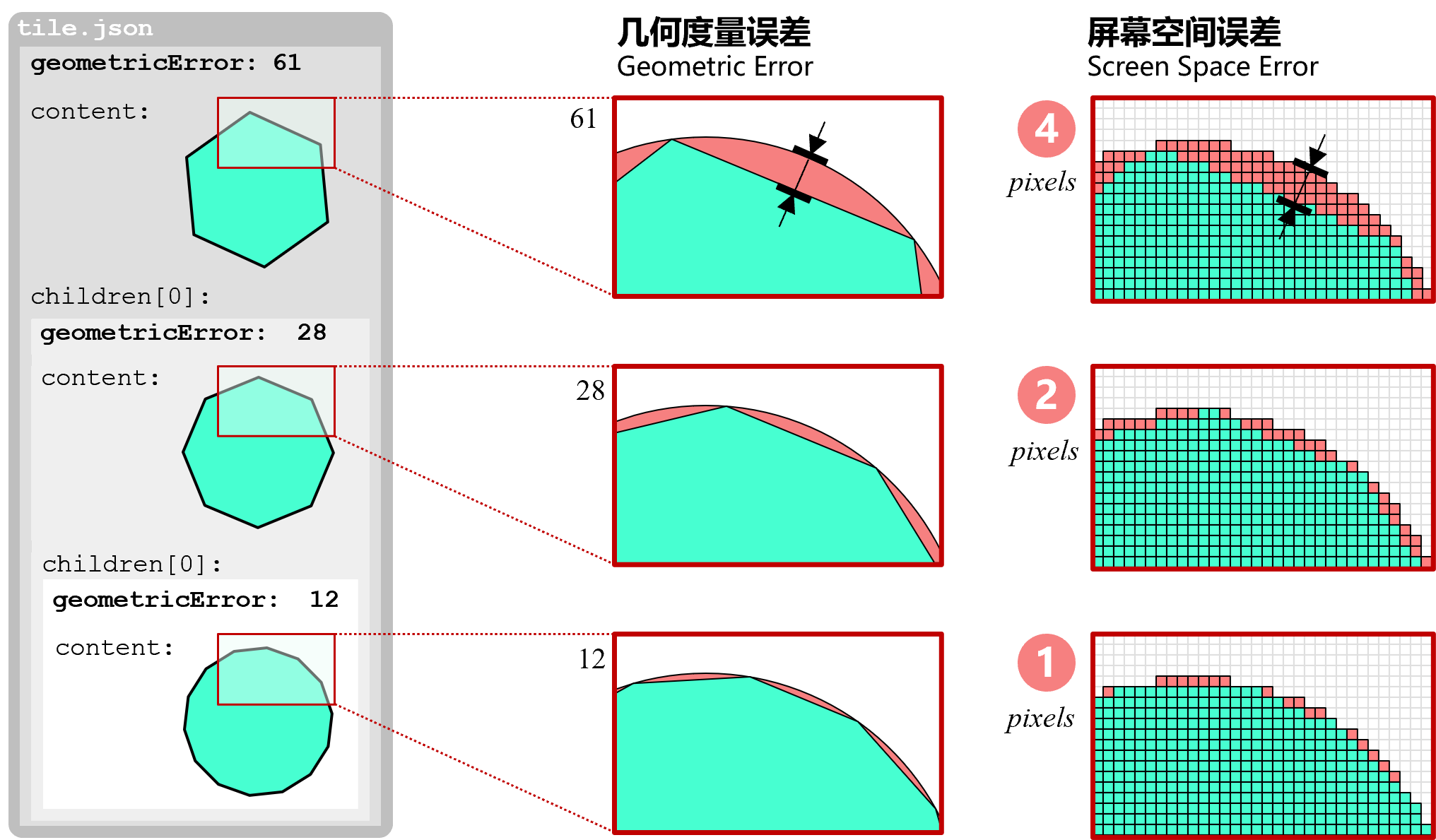
3DTiles 的设计师们在这个概念的基础上做了一件很有意思的事情,他们将这个几何度量误差与层次化细节模型紧密衔接在一起,用几何度量误差来敲定层次化细节模型的加载时机和加载顺序。所谓的层次化细节层次模型,其英文全称为 Hierachical Level of Detail,也即 HLOD,可以理解为细节层次模型的一类变种:
LOD,Level of Detail,细节层次模型
根据距离用一个模型代替另一个模型,当距离该模型远的时候,可以用一个面数更少的模型来代替之前的模型来较少渲染损耗。这个过程需要额外的一次绘制调用。HLOD,Hierarchical Level of Detail,层次化细节层次模型
当距离足够远时,可以把多个对象组合成一个新的对象,这个新的对象是一个低面数的模型。
拿屏幕空间误差 SSE 作为理解 HLOD 切换的核心,可以这样解释:计算机所绘制的近似几何模型是且仅是栅格数据结构,当用户的浏览视角对近似几何模型进行放大时,几何模型的光栅化效果将会以更多的像素放大近似模型与理想数学模型之间的差距,具体呈现为屏幕空间误差 SSE 在其数值意义上的膨胀。HLOD 在这个基础上为实现屏幕误差的逐级逼近所做的事情只有一个:当屏幕空间误差 SSE 超过某一阈值时,将原来的粗略模型切换为更精细的几何模型。
那么,接下来的问题就是,如何计算出这个我们所需要的 Geometric Error 的大小呢。首先来看一下官方文档中所给出的在透视投影几何中, SSE 与 GE 之间的转换关系式:
e
s
=
e
g
⋅
H
d
⋅
2
⋅
tan
(
θ
f
/
2
)
e_{s}=\frac{e_{g}\cdot H}{d\cdot 2\cdot\tan\left(\theta_f/2\right)}
es=d⋅2⋅tan(θf/2)eg⋅H
其中,
e
s
e_{s}
es 为屏幕空间误差,
e
g
e_g
eg 为几何度量误差,
H
H
H 为以像素为单位的渲染窗口的高度,
d
d
d 为视线中心与瓦片中心之间的距离,
θ
f
\theta_f
θf 为视场角的大小。参照 jdq0603 博客《3DTile 的geometricError含义》的理解可以绘制出一个关于 Geometric Error 和 Screen Space Error 之间转换关系的示意图:

据此,可根据相似三角形以及三角函数的相关公式推知:
e
s
=
d
′
⋅
e
g
d
=
H
2
tan
(
θ
f
/
2
)
⋅
e
g
d
=
e
g
⋅
H
d
⋅
2
⋅
tan
(
θ
f
/
2
)
e_s=d'\cdot\frac{ e_g}{d}=\frac{H}{2\tan(\theta_f/2)}\cdot\frac{e_g}{d}=\frac{e_{g}\cdot H}{d\cdot 2\cdot\tan\left(\theta_f/2\right)}
es=d′⋅deg=2tan(θf/2)H⋅deg=d⋅2⋅tan(θf/2)eg⋅H
显然,这里的转换关系针对的是具体的数值而非 jdq0603 的博客所理解的物体的半径大小,也就是说这个公式中并没有体现出上文所提到的几何度量误差的实际意义,其代表的是数值映射关系,而非 Geometric Error 的抽象指代。秋意正寒的《3dTiles 几何误差详解》一文所指出几何度量误差的计算是一个依赖于经验值的东西,其大小与观察距离有一定程度的联系,其提供了这样一个经验公式:
e
g
=
f
(
d
)
≈
d
×
0.56
×
16
÷
936
=
0.00957
⋅
d
e_g=f(d)\approx d\times0.56\times 16 \div 936=0.00957\cdot d
eg=f(d)≈d×0.56×16÷936=0.00957⋅d
























 519
519

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








