截止频率(Cutoff Frequency)是滤波器设计中的一个重要参数,用于定义滤波器在不同频率段的行为。具体来说,截止频率是指滤波器从通带到阻带或从阻带到通带的过渡点。不同的滤波器类型有不同的截止频率定义方式,但通常都是基于信号幅值的衰减来确定的。
滤波器的截止频率通常定义为信号幅值下降到其最大值的 − 3 -3 −3dB点。这里的 − 3 -3 −3dB是一个标准的工程术语,表示功率减少了一半。
分贝是我国法定计量单位中的级差单位,表示为dB,其定义为:“两个同类功率量或可与功率类比的量之比值的常用对数乘以10等于1时的级差” 。
根据上面的定义,分贝就是级差单位。简单来说,分贝dB用来表征两个功率的比值关系,数值上等于功率比值取对数后再乘以10。
0.707取对数再乘以20,等于 − 3 -3 −3dB。因此,当功率降为原来的一半,此时的幅值降为原来的0.707倍。
当保持输入信号的幅值不变,改变频率使输出信号降至最大值的0.707倍,即为截止频率,它是用来说明频率特性指标的一个特殊频率。输出信号幅值衰减为输入信号幅值的0.707倍时,这个频率就是截止频率。0.707是幅值的比值关系。
由于功率与幅值的平方成正比,所以当幅值下降为原来的约0.707倍时,功率减少了50%,这对应于3dB的衰减。
- 低通滤波器(Low-Pass Filter, LPF):
- 截止频率 f c f_c fc 是指高频信号开始被衰减的频率。
- 在这个频率点,信号幅值通常下降到最大值的-3dB(即功率下降为原来的一半)。
- 数学表达式: ∣ H ( j ω c ) ∣ = 1 2 ≈ 0.707 |H(j\omega_c)| = \frac{1}{\sqrt{2}} \approx 0.707 ∣H(jωc)∣=21≈0.707。

2. 高通滤波器(High-Pass Filter, HPF):
- 截止频率 f c f_c fc是指低频信号开始被衰减的频率。
- 在这个频率点,信号幅值同样下降到最大值的-3dB。
- 数学表达式: ∣ H ( j ω c ) ∣ = 1 2 ≈ 0.707 |H(j\omega_c)| = \frac{1}{\sqrt{2}} \approx 0.707 ∣H(jωc)∣=21≈0.707。

-
带通滤波器(Band-Pass Filter, BPF):
- 带通滤波器有两个截止频率:下截止频率 f c 1 f_{c1} fc1和上截止频率 f c 2 f_{c2} fc2。
- 这两个频率分别定义了通带的下限和上限。
- 在这两个频率点,信号幅值通常下降到最大值的-3dB。
- 数学表达式:
∣
H
(
j
ω
c
1
)
∣
=
∣
H
(
j
ω
c
2
)
∣
=
1
2
≈
0.707
|H(j\omega_{c1})| = |H(j\omega_{c2})| = \frac{1}{\sqrt{2}} \approx 0.707
∣H(jωc1)∣=∣H(jωc2)∣=21≈0.707。

-
带阻滤波器(Band-Reject Filter, BRF):
- 带阻滤波器也有两个截止频率:下截止频率 f c 1 f_{c1} fc1和上截止频率 f c 2 f_{c2} fc2。
- 这两个频率分别定义了阻带的下限和上限。
- 在这两个频率点,信号幅值通常下降到最大值的-3dB。
- 数学表达式:
∣
H
(
j
ω
c
1
)
∣
=
∣
H
(
j
ω
c
2
)
∣
=
1
2
≈
0.707
|H(j\omega_{c1})| = |H(j\omega_{c2})| = \frac{1}{\sqrt{2}} \approx 0.707
∣H(jωc1)∣=∣H(jωc2)∣=21≈0.707。

所以,这些截止频率想在哪在哪得有多离谱。
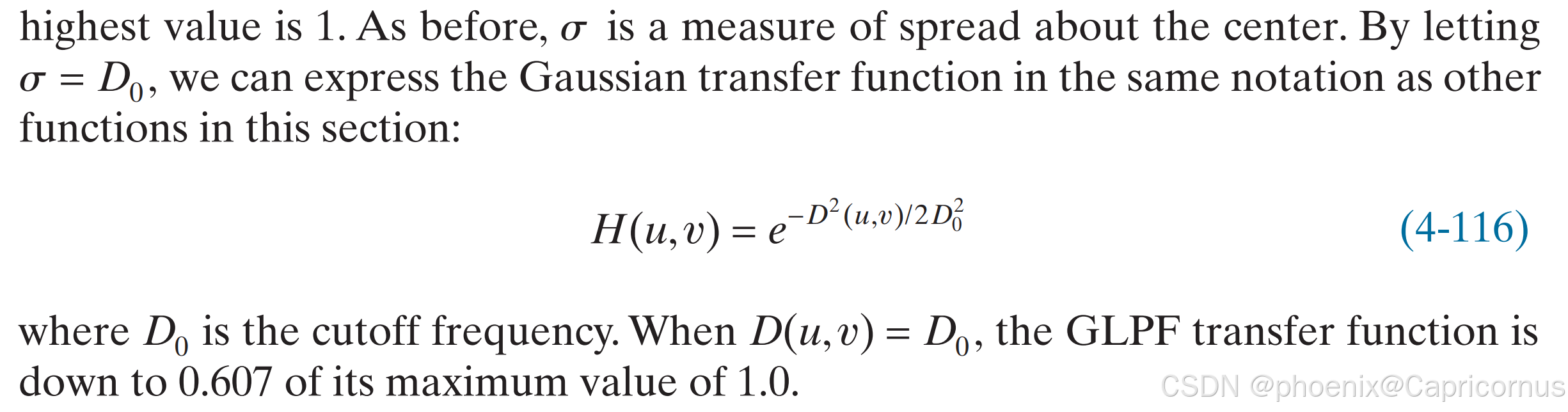



























 2553
2553

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








