艾里斑（Airy Disk）与瑞利判据（Rayleigh criterion）

有的人理解能力差，我补充一些内容。如果你理解能力差，就不要说别人有问题。秉承谦虚的态度学习。还有不懂的地方提出来，我再补充。

艾里斑的定义与形成

艾里斑（Airy Disk），又称艾里图样（Airy Pattern），是光通过圆形孔径发生衍射时，在焦点处形成的光斑。这一现象由英国数学家和天文学家George Biddell Airy在19世纪首次详细描述。

当一束平行光通过一个理想透镜时，根据几何光学的观点，理论上会在焦平面处形成一个点图像。然而，当点光源通过圆孔或圆屏衍射时，由于光的波动性质，光会在通过圆孔后发生衍射，从而在焦点处形成一个中心亮斑和周围一系列明暗相间的同心圆环向外扩散。其中，以第一暗环为界限的中央亮斑被称为艾里斑。

艾里斑的强度分布

在光学中，傅里叶变换常用于分析光的衍射和成像过程。具体来说，光的衍射图案可以看作是光波前通过某一孔径或障碍物后的傅里叶变换结果。在极坐标系下，圆域函数的傅里叶变换是贝塞尔函数。

艾里斑的光强分布可以通过一阶第一类贝塞尔函数进行数学描述。艾里斑的光强分布函数与$J_1(x)/x$的平方成正比，其中$x$是与观察角度或空间位置相关的变量。

$$I(\theta )=I_0{\left(\frac{2J_1(x)}{x}\right)}^2$$

其中，

• $I_0$是中心强度；
• $J_1(x)$是一阶第一类贝塞尔函数；
• $x=\frac{\pi D\sin (\theta )}{\lambda }$，这里$D$是孔径直径，$\theta$是相对于中心轴的角度，$\lambda$是光的波长。

一阶贝塞尔函数 $J_1(x)$的定义可以通过下面的无穷级数给出：

$$J_1(x)=\sum _{m=0}^{+\infty }\frac{(-1{)}^m}{m!\Gamma (m+2)}{\left(\frac{x}{2}\right)}^{2m+1}$$

在这个级数中：

• $m$是非负整数索引，
• $(-1{)}^m$表示项的符号随 $m$增加而交替变化，
• $m!$是 $m$的阶乘，即 $m\times (m-1)\times ...\times 1$，
• $\Gamma (m+2)$是伽玛函数，它是阶乘的推广，适用于所有实数和复数（除了负整数）。特别地，对于正整数 $n$，有 $\Gamma (n+1)=n!$，
• $x$是变量。

这个级数收敛于一阶贝塞尔函数 $J_1(x)$，并且提供了计算该函数值的一种方法。需要注意的是，虽然这个级数看起来复杂，但在实际应用中，通常只需要计算有限几项就可以得到足够精确的结果。

贝塞尔函数是一类在波动问题、圆柱坐标和球坐标中的势函数、量子力学中的径向波函数等问题中常出现的特殊函数。它们满足贝塞尔微分方程，是这类方程的解。贝塞尔函数有多种，其中最常见的是第一类贝塞尔函数（Bessel function of the first kind），记作$J_{\alpha }(x)$，其中$\alpha$为阶数。当$\alpha$为整数时，如$\alpha =1$，即得到一阶第一类贝塞尔函数$J_1(x)$。

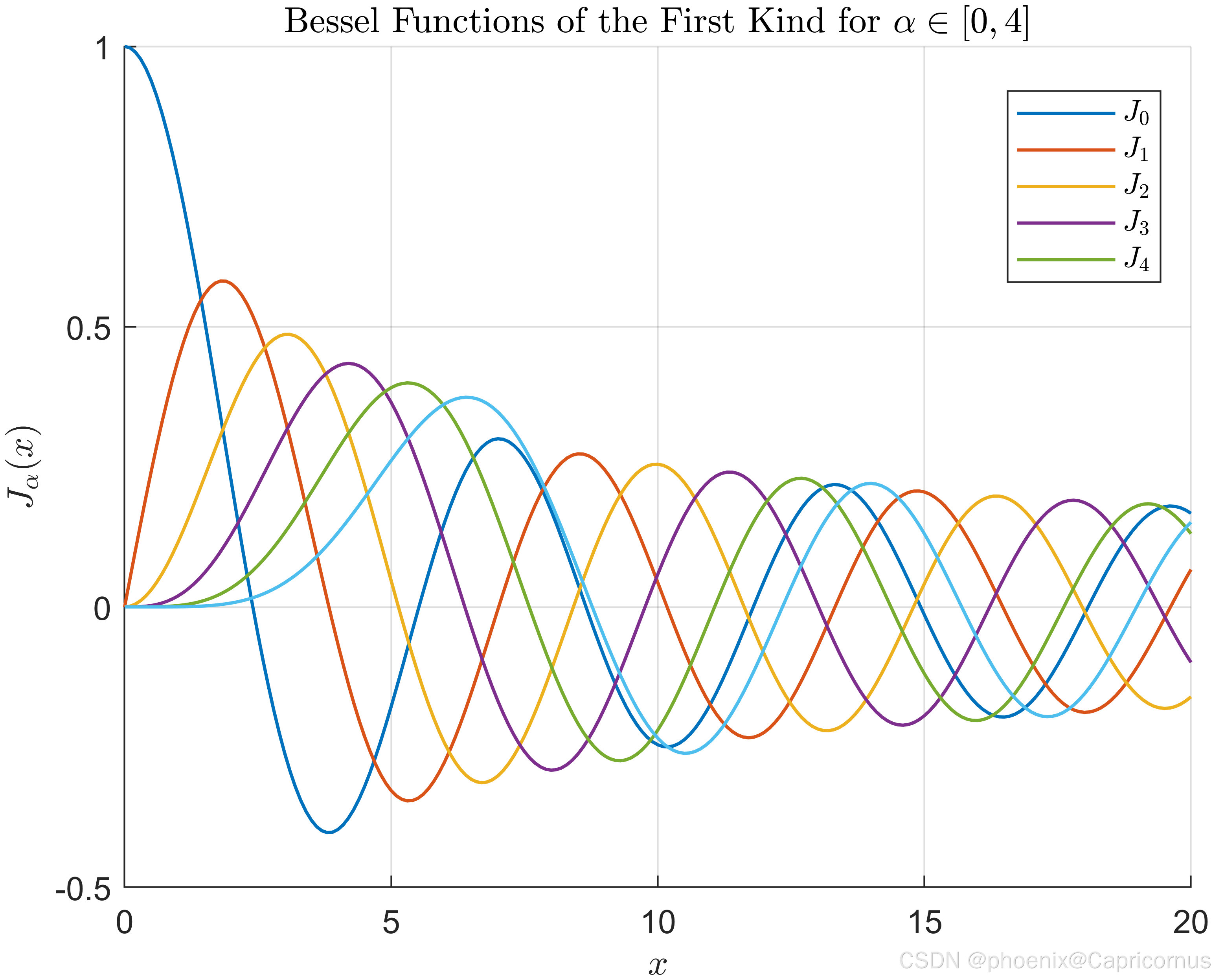
艾里斑的光强分布函数

一阶第一类贝塞尔函数在艾里斑的形成中起到了关键作用。它不仅描述了艾里斑中心亮斑的光强分布，还通过其零点位置确定了艾里斑的半径以及周围衍射环的位置。这种关系不仅揭示了艾里斑形成的物理机制，还为我们在光学、波动学等领域的研究提供了重要的数学工具。

光学分辨率

在光学成像系统中，分辨率是指系统区分两个相邻物体的能力。在实际的光学成像系统中，艾里斑的出现会导致图像的分辨率下降，因为它限制了光学系统的分辨能力。

瑞利判据

瑞利判据（Rayleigh criterion）在衍射极限系统当中定义了分辨率极限，换言之，何时能够将两个点光源相互区分或分辨。

使用艾里斑理论，如果两个单独艾里斑的衍射图案不重叠，则就可以轻松区分、‘分辨’两者并认定满足瑞利判据。而当艾里斑的中心直接重叠于另一个艾里斑的第一个暗环时，则两者认定为‘刚好分辨’，同时依然可以区分为两个独立的点光源。如果艾里斑再继续相互接近，则两者无法满足瑞利判据，因此“无法被分辨”为两个不同的点光源。

根据瑞利判据，一个点光源艾里斑的中央主极大与近旁的另一个艾里斑的第一个暗环重合，以此作为光学系统的分辨率极限，这个距离恰好就是艾里斑半径。也就是两个物点的距离必须大于或等于艾里斑直径的一半，才能被视为可分辨的。

光学系统的分辨率可以通过计算艾里斑的半径来确定，这个半径称为艾里斑的半角宽度。艾里斑的第一个暗环对应的半角宽度（half-angle width）可以用来量化光学系统的分辨率。在理想情况下，如果两个物点产生的艾里斑的中心之间距离小于艾里斑的半角宽度，那么这两个物点就无法被分辨开。因此，艾里斑的存在决定了光学系统的最高分辨率。

艾里斑的第一个暗环出现在$J_1(x)$首次过零点的位置。这个过零点的位置大约在 $x=3.8317$，这是第一阶贝塞尔函数的第一个零点。由此可以得到半角宽度 ${\theta }_A$的计算公式：

$${\theta }_A=\arcsin \left(\frac{3.8317\lambda }{\pi D}\right)\approx 1.22\frac{\lambda }{D}$$

这里用了近似值 $\arcsin (3.8317/(\pi D))\approx 1.22\lambda /D$，这是因为对于小角度，$\arcsin (x)\approx x$。

半角宽度${\theta }_A$可以用下面的公式来计算：

$${\theta }_A=1.22\frac{\lambda }{D}$$

其中，

• $\lambda$是光的波长；
• $D$是孔径的直径（例如透镜的直径）。

${\theta }_A$称为最小分辨角。分辨力与${\theta }_A$成反比。

• 波长越短，半角宽度${\theta }_A$越小，分辨率越高。因此，使用较短波长的光可以提高分辨率。例如，紫外线的波长比可见光短，因此使用紫外线可以获得更高的分辨率。
• 孔径越大，半角宽度${\theta }_A$越小，分辨率越高。因此，增大孔径直径可以提高分辨率。这就是为什么高分辨率的显微镜和望远镜往往会有较大孔径的原因。

分辨率极限

对于小角度，$\tan \theta \approx \theta$。根据瑞利判据，两个物点之间的距离$d$

$$\frac{d}{L}=1.22\frac{\lambda }{D}$$

称为光学系统的分辨率极限。其中$L$是物点到透镜的距离。当两个物点之间的距离小于或等于这个值时，光学系统将无法将它们分辨开来。物点距离透镜越远，分辨率极限$d$也会相应增大。