信号移位或补零不会改变卷积的结果——卷积的时移性质（答作者问）

廖老师认为图(b)和图©与信号卷积的结果不同。

答：图©只是图(b)的移位加补零，都不会改变卷积的有效结果。

卷积的时移性质适用于连续时间信号和离散时间信号，如果对参与卷积的一个信号进行时移，那么卷积的结果也会相应地发生相同的时移。

连续时间卷积的时移性质

对于两个连续时间信号$f(t)$和$h(t)$，它们的卷积定义为：
$$(f\ast h)(t)={\int }_{-\infty }^{\infty }f(\tau )h(t-\tau )d\tau$$

如果我们对$f(t)$或$h(t)$中的任何一个应用一个时间延迟$t_0$，即$f(t-t_0)$或$h(t-t_0)$，那么卷积结果将会是原卷积结果的时间平移$t_0$：
$$(f(t-t_0)\ast h(t))(t)=(f\ast h)(t-t_0)$$
$$(f(t)\ast h(t-t_0))(t)=(f\ast h)(t-t_0)$$

在卷积运算中，任何一个输入信号的时间平移将直接导致输出信号相同量的时间平移。

离散时间卷积的时移性质

在离散时间域中，我们处理的是序列而不是连续函数，并且时间延迟通常表示为整数个样本点。假设我们有两个离散时间序列$x[n]$和$h[n]$，它们的离散卷积定义为：
$$y[n]=(x\ast h)[n]=\sum _{k=-\infty }^{\infty }x[k]h[n-k]$$

如果我们对$x[n]$或$h[n]$中的任何一个应用一个时间延迟$n_0$（即$x[n-n_0]$或$h[n-n_0]$），那么卷积结果将会是原卷积结果的时间平移$n_0$：
$$(x[n-n_0]\ast h[n])=y[n-n_0]$$
$$(x[n]\ast h[n-n_0])=y[n-n_0]$$

在离散卷积中，任何一个输入序列的时间平移会导致输出序列相同量的时间平移。

时域前面补零是移位，时域末尾补零就是增加了卷积结果长度。

时域末尾补零通常有两个作用，很重要。

• 利用离散傅里叶变换（DFT）实现线性卷积。见线性卷积和循环卷积等效的条件。
• 在频域增加采样密度，见频率间隔、频率分辨率与频率采样密度。

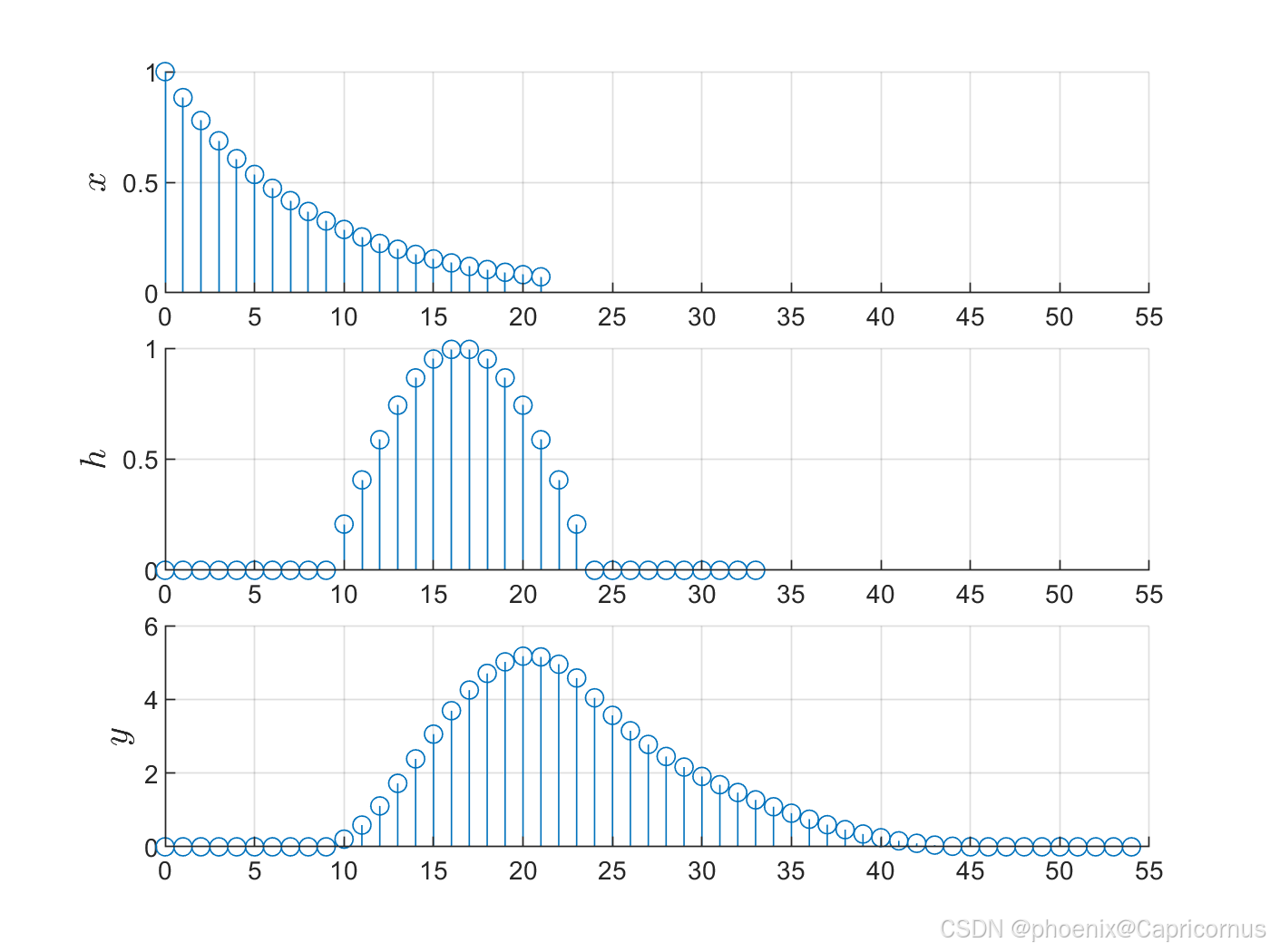
总结

无论是连续时间还是离散时间卷积，时移性质都表明了同样的原理：对卷积中的任一函数或序列应用时移，等同于对卷积结果应用相同的时移。