RevIN 时间序列预测可逆实例归一化论文笔记 ICLR 2022

特别闹

已于 2024-12-19 14:34:13 修改

阅读量1.9k

点赞数 34

文章标签：论文阅读深度学习人工智能算法数据挖掘

于 2024-10-25 15:06:53 首次发布

本文链接：https://blog.csdn.net/u013611278/article/details/143116621

版权

# 这个笔记写的可能有点仓促，有空再补

文献地址：https://openreview.net/pdf?id=cGDAkQo1C0p

代码地址：GitHub - ts-kim/RevIN: RevIN: Reversible Instance Normalization For Accurate Time-series Forecasting Against Distribution Shift

在时间序列中，均值和方差等统计属性经常随时间变化，即时间序列数据存在分布移位问题。也就是说，对于不同滑动窗口，其内部的均值和方差不是固定的，会随着时间而变化。

时间序列的归一化操作，我们可以采用StandardScaler, MinMaxScaler, MaxAbsScaler..…，但是通常我们是基于历史的整体观察序列来计算max, min，mean, std等统计量，有时候在推理阶段的反归一化往往会产生数据分布的概念性漂移，如下图这样：

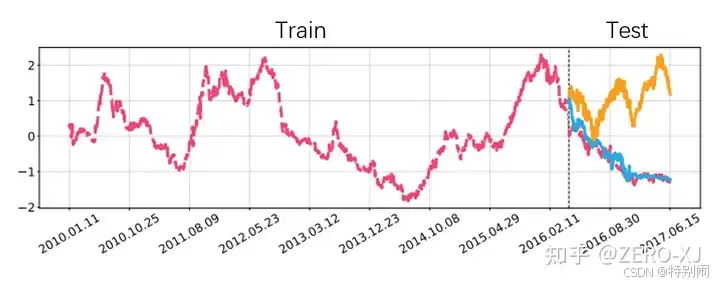
我们需要的预测结果是蓝色线条，但是结果往往倾向于橙色的结果，也就是说预测模型的训练数据和测试数据的分布不一致。

(上图来源知乎文章：https://zhuanlan.zhihu.com/p/528990583)

如果我们从输入序列中去除非平稳信息，即实例的均值和标准差，则会减少数据分布中的差异，从而提高模型的性能。然而，将这种归一化应用于模型输入可能会导致另一个问题，因为它可能会阻止模型捕获原始数据分布。它消除了在预测任务中对预测未来值很重要的非平稳信息。

文章提出了一种简单而有效的归一化和反规范化方法——可逆实例归一化（RevIN），该方法首先对输入序列进行归一化，然后对模型输出序列进行反规范化，以解决分布移位的时间序列预测问题。

问题描述

时间序列数据的统计特性（如均值和方差）随时间变化而变化，这种现象被称为分布偏移（distribution shift）。分布偏移是导致时间序列预测模型性能下降的主要原因之一，因为它会在训练和测试数据之间造成差异。

时间序列预测模型往往受到时间序列数据中一个独特特征的严重影响：它们的统计特性，如均值和方差，会随着时间的推移而变化。这被广泛称为分布偏移问题，它可能会在预测模型的训练数据和测试数据的分布之间产生差异。在时间序列预测任务中，训练和测试数据通常根据特定时间点从原始数据中分割出来。因此，它们通常几乎不重叠，这是模型性能下降的常见原因。此外，模型的输入序列也可以具有不同的潜在分布。我们可以假设，不同输入序列之间的差异会显著降低模型性能。

在这种假设下，如果我们从输入序列中去除非平稳信息，特别是实例的均值和标准差，数据分布的差异将减小，从而提高模型性能。然而，将这种归一化应用于模型输入可能会导致另一个问题，因为它会阻止模型捕获原始数据分布。它删除了在预测任务中对预测未来值很重要的非平稳信息。该模型只需要使用归一化输入来重建原始分布，由于固有的局限性，这会降低其预测性能。

方法

可逆实例规范化

输入一个向量x，即它实际上可以看作一个多变量，每一个维度可以看作一个单变量。x通过RevIN，将b-1的分布转换到b-2，可以看到它的均值发生了改变，每一个单变量都针对均值做了归一化，这样原始分布中不同单变量之间的分布差异被人为的减少。将变换分布后的 $\hat x$ 当作输入给网络，输出 $\tilde y$ ，这些 $\tilde y$ 具有 b-3的分布，但也许不符合真实的分布。所以a-1的RevIN中间有一些参数，其中代表均值和方差就不提了，β是进行归一化的参数，γ是进行仿射变换的可学习参数。通过这些参数，b-3通过RevIN做一次reversing，回归近似真实的分布b-4。

其中均值和方差的计算（1）已给出。而具体的归一化公式（2）也给出，减均值除标准差后乘γ加上β。

$\hat{y}_{kt}^{(i)}=\sqrt{\mathrm{Var}[x_{kt}^{(i)}]+\epsilon}\cdot\left(\frac{\tilde{y}_{kt}^{(i)}-\beta_{k}}{\gamma_{k}}\right)+\mathrm{E}_{t}[x_{kt}^{(i)}].$

简单地添加到网络中的虚拟对称位置，RevIN可以有效地缓解时间序列数据中的分布差异，作为任意深度神经网络的通用可训练归一化层。事实上，所提出的方法是一种灵活的、端到端的可训练层，可以应用于任何任意选择的层，甚至是几层。我们通过将其添加到附录a.4表7中模型的中间层来验证其作为柔性层的有效性。然而，当应用于编码器-解码器结构的虚拟对称层时，RevIN是最有效的。在典型的时间序列预测模型中，编码器和解码器之间的边界通常不清楚。因此，我们将RevIN应用于模型的输入和输出层，因为它们可以被解释为编码器-解码器结构，在给定的输入数据下生成后续值。

可逆实例规范化对分布移位的影响

在原始输入（图3(a)）中，训练数据和测试数据的分布几乎没有重叠（尤其是ETTm1），这是由分布移位问题造成的。此外，每个数据分布都有多个峰值（特别是ETTh1和ECL的测试数据），这意味着数据中的序列在分布上可能存在严重的差异。然而，在本文提出的方法中，归一化步骤将每个数据分布转换为以均值为中心的分布（图3(b)）。这一结果支持了原始的多模态分布（图3(a)）是由数据中不同序列之间的分布差异造成的。更重要的是，该方法使训练数据和测试数据分布重叠。验证了RevIN的归一化步骤可以缓解分布偏移问题，减少训练数据与测试数据之间的分布差异。

将归一化后的数据作为输入，模型可以在预测输出中保留对齐的训练数据和测试数据分布（图3(c)），然后通过RevIN的反规范化步骤返回到原始分布（图3(d)）。在不进行反规范化的情况下，模型只需要使用归一化输入来重建遵循原始分布的值（图3(d)），该输入遵循转换后的分布，其中去除了非平稳信息（图3(b)）。此外，我们假设，当RevIN仅应用于输入和输出层时，模型中间层的分布差异也会减少。因此，这个RevIN过程可以认为是先使问题变得简单，然后再将问题恢复到原来的状态，而不是直接解决存在分布移位问题的挑战性问题。

RevIN作为一种普遍适用于任意深度神经网络的可训练归一化层，简单地添加到网络中几乎对称的位置，可以有效地缓解时间序列数据的分布差异。实际上，所提出的方法是一个灵活的、端到端可训练的层，可以应用于任何任意选择的层，甚至几个层。

RevIN在应用于编码器-解码器结构的几乎对称层时是最有效的。在典型的时间序列预测模型中，编码器和解码器之间的边界通常是不明确的。因此，我们将RevIN应用于模型的输入和输出层，因为它们可以解释为编码器-解码器结构，在给定输入数据的情况下生成后续值。

论文里提到这种过网络之前先过RevIN的结构相比传统的BN使用，更像是Encoder-Decoder，将RevIN解读维编码器/解码器也许会更好。这种层的作用并不是直接解决层间更新参数分布的偏移问题，而是有点像传统机器学习中的归一化，先清洗数据，最后反回来求。

即RevIN是一种模型无关的方法。

Experiments

结果狠狠upup

参考资料

时间序列（反）归一化 RevIN

【边读边写】Reversible Instance Normalization for Accurate TSF Against Distribution Shift

【深度学习】时序偏移归一化利器-RevIN_revin 归一化-CSDN博客

时序建模基础——RevIN-CSDN博客