[RLinear]Revisiting Long-term Time Series Forecasting: An Investigation on Linear Mapping 论文笔记

特别闹

已于 2024-11-26 09:32:16 修改

阅读量1.5k

点赞数 18

文章标签：论文阅读深度学习人工智能机器学习论文笔记时序数据库

于 2024-11-21 15:42:43 首次发布

本文链接：https://blog.csdn.net/u013611278/article/details/143920892

版权

论文地址：https://arxiv.org/abs/2305.10721

论文标题：Revisiting Long-term Time Series Forecasting: An Investigation on Linear Mapping

代码：GitHub - plumprc/RTSF: Revisiting Long-term Time Series Forecasting: An Investigation on Linear Mapping

paperswithcode:https://paperswithcode.com/paper/revisiting-long-term-time-series-forecasting

其实主要的代码就是RevIN加上了线性层，但是论文内有很多理论分析，很充分

前序工作

Linear-LSTF ( DLinear / NLinear )

2022 AAAI《Are transformers effective for time series forecasting?》表明，这些基于Transformer的方法可能不如以前认为的那么有效，并发现与自回归生成相比，它们报告的预测结果可能主要依赖于单次预测。相反，仅使用单个线性层的LTSF-Linear令人惊讶地大大优于现有的复杂架构。后续的方法抛弃了编码器-解码器架构，专注于开发时间特征提取器，并对历史输入和预测之间的映射进行建模。虽然这些方法提高了预测性能，但它们仍然没有明显优于线性模型。此外，它们通常需要大量可调的超参数和特定的训练技巧，如归一化和通道特定处理，这可能会影响比较的公平性。

ReVIN( Reversible instance normalization )

时间序列预测中的主要挑战之一是数据分布漂移问题（distribution shift problem），即数据分布，比如数据的均值方差等，会随着时间而变化，这会给时序预测问题造成一定的难度（这类数据也成为非平稳数据non-stationary）。而在时序预测任务中，训练集和测试集往往是时间来划分的，这天然会引入训练集和测试集分布不一致的问题，此外，不同输入序列也会有数据分布不一致的问题。这两个不一致的问题都可能会导致模型效果的下降。为了解决上述问题，可以想办法去除数据中的非平稳信息，但是如果只是简单的消除非平稳信息，因为它可能会阻止模型捕获原始数据分布，会导致非平稳信息丢失。

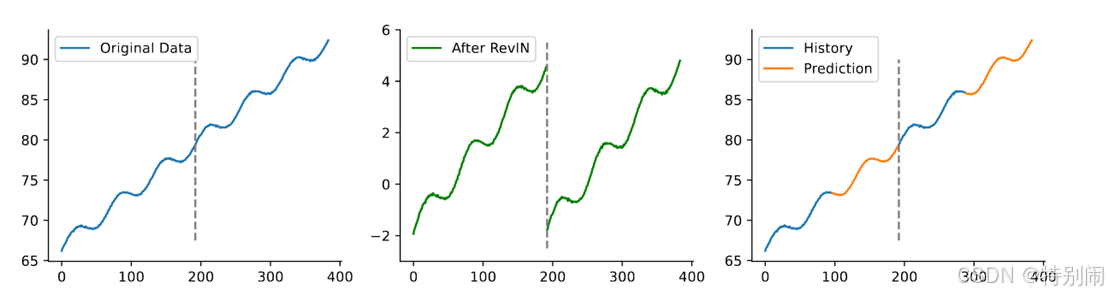
数据分布漂移导致我们期望在Test阶段的预测曲线是蓝色线条，但是结果会成为橘色的线条！因此导致预测模型的训练数据和测试数据的分布不一致。

2022 ICLR《Reversible instance normalization for accurate time-series forecasting against distribution shift》文章提出了一种简单而有效的归一化和反规范化方法——可逆实例归一化（RevIN），该方法首先对输入序列进行归一化，然后对模型输出序列进行反规范化，以解决分布移位的时间序列预测问题。RevIN是一个灵活的端到端可训练的层，可以应用于任何任意选择的层，有效地抑制一层中的非平稳信息（实例的均值和方差），并在另一层中几乎对称的位置恢复它，例如输入和输出层。

时间特征提取器的有效性

“RLlinear”是指具有RevIN的线性投影层。Fixed random extractor意味着我们只随机初始化时间特征提取器，在训练阶段不更新其参数。值得注意的是，RevIN显著提高了这些方法的预测准确性。借助RevIN，即使是简单的线性层也可以超越先进的baseline PatchTST。即使使用具有未经训练参数的随机初始化时间特征提取器，也可以得到有竞争力的、甚至更好的预测结果。有必要考虑这些特征提取器从时间序列数据中学到了什么。

时间序列预测中的线性映射

当时间特征提取器是MLP时，MLP和投影层都会学习混沌权重，而两者的乘积与从单个线性层学习的权重保持一致。另一方面，当时间特征提取器是attention时，它也会学习混乱的权重，但投影层学习的权重与单个线性层的权重相似，这意味着线性投影在时间序列预测中的重要性。

为了减轻任何潜在的数据集特定偏差，作者使用与PatchTST相同的比较方式，在完整的ETT基准上进行了更多的实验。

与精心设计的方法相比，简单的基线RLlinear在大多数情况下具有相当甚至更好的性能。有时，这些使用时间特征提取器的精细模型甚至比未经训练的原型表现更差。值得注意的是，具有固定随机时间特征提取器的模型通常表现出相似的预测性能，并且接近单个线性层。

观察结果促使我们质疑时间特征提取器是否必要，以及为什么线性映射在长期时间序列预测中如此有效。

线性映射的理论与实证研究

线性映射学习周期性

单个线性层也可以有效地学习周期性模式。

考虑一个单一的线性层为 $Y=WX+b$ (1)

其中 $W\in R^{n\times\mathfrak{m}}$ 是权重，也称转移矩阵 $b\in R^{1\times\mathfrak{m}}$ 是偏置

假设1：一般的时间序列 $x(t)$ 可以被分解为季节性部分 $s(t)$ 和趋势部分 $f(t)$ ，并带有可容忍的噪声，表示为 $x(t)= s(t)+ f(t)+ \epsilon$

定理1：给定一个满足 $x(t)=s(t)=s(t-p)$ 的季节性时间序列，其中 $p\leq n$ 是周期，线性模型总是存在一个分析解

$\begin{aligned}&[x_{1^{\prime}},x_{2^{\prime}},\cdots,x_{n}]\cdot W+b=[x_{n+1^{\prime}},x_{n+2^{\prime}},\cdots,x_{n+m}]&\text{(2)}\\&W_{ij}^{(k)}=\begin{cases}1,&if i=n-kp+(j mod p)\\\\0,&otherwise\end{cases}&\text{(3)}\end{aligned}$

上述方程表明，当输入历史序列的长度不小于周期时，线性映射可以预测周期信号，但这不是唯一的解。由于 $s(t)$ 中每个时间戳对应的值几乎不可能线性独立，因此W参数的解空间很广。特别是，当 $n\gg p$ 时，可以获得具有不同因子 $k$ 的 $W^{(k)}$ 的更多潜在值的闭式解。带有适当比例系数的 $[W^{(1)},\cdots,W^{(k)}]$ 的线性组合也满足上述方程的解。

推论1.1：当给定的时间序列满足 $x(t)=ax(t-p)+c$ ,其中a、c是缩放和平移因子时，线性模型仍然具有方程2的闭式解，如下所示

因此我们知道，单个线性层可以有效地捕捉时间序列中的周期性。

图中显示的权重也支持我们的观点，即从输入到输出的转换矩阵显示出明显的周期性（每个周期24个时间步长）。然而，在实践中，时间序列通常遵循假设1，因此趋势项可能会影响线性模型的学习。下图展示了线性层对模拟的季节和趋势信号的预测结果，包括正弦波、线性函数及其总和。正如预期的那样，线性模型很好地适应了季节性，但在趋势方面表现不佳，无论它是否有偏差项。

线性模型在趋势预测中表现不佳

TSMixer也研究了类似的问题，并提供了线性模型在预测具有季节和趋势成分的时间序列时的性能上限。基于他们的工作，作者调整了他们的结论，并推导出了以下定理。

定理2：设 $x(t)=s(t)+f(t)$ 其中 $s(t)$ 是一个周期为𝑝的季节性信号， $f(t)$ 满足K-Lipschitz连续，那么存在一个如方程2的线性模型，输入长度 $n=p+\tau,\tau\geq 0$ ，得到

$|x(x+j)-\hat{x}(n+j)|\leq K(p+j),j=1,\ldots,m$

证明：

为了简化证明过程，我们假设历史数据的时间戳是1到n，那么对于要预测的第j个真实值 $x(n+j)$ ，我们有 $x(n+j)=x(p+\tau+j)=s(\tau+j)+f(p+\tau+j)$

假设线性模型只能学习周期性模式，我们可以直接使用方程3作为近似解，其中我们选择 $k=1$ ，因此对于 $x(n+j)$ 的预测是

$\hat{x}(n+j)=XW+b=x\big(n-p+(j mod p)\big)=s(\tau+j)+f\big(\tau+(j mod p)\big)$

利用K-Lipschitz连续的特性，我们可以得到

$\begin{aligned} |x(n+j)-\hat{x}(n+j)|& =\left|f(p+\tau+j)-f\big(\tau+(j mod p)\big)\right| \\ &\leq K|p+j-(j\bmod p)| \\ &\leq K(p+j) \end{aligned}$

尽管趋势项的线性模型的预测误差是有界的，但随着时间戳的累积或趋势项变得更加重要，它仍然会影响预测结果。这可能是线性模型在趋势预测中表现不佳的原因。

利普希茨连续。满足如下性质的任意连续函数 f 称为 K-Lipschitz： $\parallel f(x_{1})-f(x_{2})\parallel\leq K\parallel x_{1}-x_{2}\parallel,\forall x_{1},x_{2}\in\mathrm{dom}f$

这个条件实际上限制了函数变化的速率，确保了函数在任意两点之间的变化不会超过一个固定的倍数。K被称为Lipschitz常数，它是一个非负实数。

在DL中，由于 Lipschitz continous 的函数的梯度上界被限制，因此函数会更平滑。因此利用梯度下降进行参数更新时，参数的变化不会太大/剧烈从而降低梯度爆炸的发生概率，使模型的更新更稳定。

去纠缠与规范化

分解的问题

如果可以消除趋势项或将其与季节项分离，则可以提高预测性能。之前的工作侧重于将时间序列分解为季节性和趋势性成分，以单独预测它们。一般来说，他们利用由具有适当大小的滑动窗口的平均池层实现的移动平均来从输入时间序列中获取趋势信息。然后，他们从原始数据中减去趋势项得到的周期性信号中识别出季节特征。（Autoformer中用到的方法）

然而这些解缠结方法存在一些问题。首先，滑动窗口大小应大于季节性部分的最大周期，否则解耦将不足。其次，由于使用了平均池化层，对齐需要在输入时间序列的两端进行填充，这不可避免地会扭曲序列的头部和尾部。此外，即使信号完全解开，或者它们只有趋势项，欠拟合趋势项的问题仍然存在。因此，虽然解纠缠可以提高预测性能，但它与最近的一些先进模型仍有差距。

将趋势转化为季节性

由于分布偏移问题，时间序列的一些统计信息，如均值和方差，会随着时间的推移而不断变化。为了应对这一挑战，RevIN是一种方法，它首先对输入的历史时间序列进行归一化，并将其输入到预测模块中，然后对最终结果的预测进行非归一化。下图是使用不同归一化方法对两个通道的模拟趋势信号的预测结果。使用Batch Normalization和分解都没有太好的效果，而在RevIN的帮助下，单个线性层可以准确地预测趋势项。

可逆归一化的核心在于可逆性。它消除了由矩统计引起的趋势变化，同时保留了可用于恢复最终预测结果的统计信息。

对于季节性信号，RevIN会缩放范围，但不会改变周期性。对于趋势信号，RevIN将每个分段缩放到相同的范围内，并表现出周期性模式。RevIN能够将一些趋势转化为季节性，使模型更好地学习或记忆趋势。RevIN将不断变化的趋势转换为具有固定和相似趋势的多个细分部分，展现出周期性特征。因此，可以减轻过去累积时间步长引起的趋势预测误差，从而获得更准确的预测结果。

实验评估

实验结果

鉴于RevIN显著提高了预测性能，作者添加了两个简单的baseline，分别是RLlinear和RMLP，带有两个线性层和一个ReLU，以进行更公平的比较。对比的baseline是PatchTST (ICLR 2023), TimesNet (ICLR 2023), and DLinear (AAAI 2023)。

在具有大量通道的数据集（如天气和ECL）上，RLlinear的性能并不明显优于复杂模型。主要是多重周期性的问题。

线性模型在通道之间遇到多个周期时

尽管线性映射能够学习时间序列中的周期性，但在处理多通道数据集时仍面临挑战。

为了解决这个问题，一种可能的解决方案是使用通道独立（CI）建模，该建模独立地处理时间序列中的每个通道。虽然这种方法可以提高预测精度，但也会显著增加计算开销。

观察到RLlinear CI和RMLP能够拟合曲线，而RLlinear则失败了。这表明，单个线性层可能难以学习通道内的不同周期。非线性单元或CI建模可用于增强具有不同周期通道的多元时间序列模型的鲁棒性。

单个线性层可能容易受到信道之间不同周期的影响。

为了进一步研究线性映射对多元时间序列的影响，使用一系列角频率在1/30到1/3之间、长度为3000的正弦波进行了模拟。

线性模型在具有两个通道的时间序列上表现良好，无论周期性的差异是小还是大。

随着具有不同周期的信道数量的增加，线性模型的性能逐渐变差，而具有非线性单元或CI的模型继续表现良好。此外，增加输入范围会明显地降低线性模型在多通道数据集上的预测性能。

现有的模型可能侧重于学习季节性，多元时间序列中不同通道之间的周期性差异是制约预测性能的关键因素。

定理3 $X=[s_1,s_2,\cdots,s_C]^T\in R^{c\times n}$ 是输入的历史多变量时间序列，有 $c$ 个通道，长度为 $n$ 。如果每个信号 $s_i$ 都有相应的周期 $p_i$ ，则必须有一个线性模型 $Y=XW+b$ ，当 $n\geq lcm (p_{1},p_{2} \ldots , p_{c})$ 时，可以预测下一个 $m$ 个时间步

(lcm是最小公倍数Least Common Multiple)

如上图所示，增加输入范围可以显著提高预测性能。这是因为较长的输入范围覆盖了更多的潜在周期，从而最大限度地缩小了线性模型和具有非线性单元的模型之间的性能差距。但当输入范围较长时，RLinear-CI和RMLP在ETTh1数据集上的表现较差，这可能是由于该特定数据集的体积较小。

此外，应该指出的是，通过增加输入范围实现的性能改进存在上限。这一限制可能高度依赖于数据集中存在的周期性模式。

参考资料

重新审视长时间序列预测：关于线性映射的调查_revin-CSDN博客

时间序列（反）归一化 RevIN - 知乎