注: 本文分两部分,原文在前,译文在后,译文来自中国物理学会期刊网。
–
Stubborn equations and the study of symmetry
Marianne Freiberger
Submitted by Marianne on 22 October, 2014

Niels Henrik Abel.
In 1824 a young Norwegian mathematician called Niels Henrik Abel proved a shocking result involving a certain type of equation. A little later the French prodigy Évariste Galois provided deep insight into why that result was true — and in the process founded the mathematical study of symmetry. Neither of the two lived long to enjoy the fruits of their work. Abel died in 1829, at the age of 26, from tuberculosis and in poverty. Galois died in 1832, from wounds he received in a duel allegedly fought over a woman. He was only twenty years old.
So what was their work about? And what do equations have to do with symmetry?
Solving equations
One of the most famous mathematical formulas is the one that gives you the solution to a quadratic equation. If the equation is a x 2 + b x + c = 0 ax^2 + bx +c =0 ax2+bx+c=0 then the formula tells you that the solutions are x 1 = − b + b 2 − 4 a c 2 a x_1 = \frac{-b+\sqrt{b^2-4ac}}{2a} x1=2a−b+b2−4ac and x 2 = − b − b 2 − 4 a c 2 a . x_2 = \frac{-b-\sqrt{b^2-4ac}}{2a}. x2=2a−b−b2−4ac. No matter what a a a, b b b and c c c are, this formula hands you the solution on a plate. It’s very handy.
There is a similar formula, though a lot more complicated (see here), which gives you a general solution to a cubic equation of the form
a x 3 + b x 2 + c x + d = 0. ax^3 + bx^2 + cx +d =0. ax3+bx2+cx+d=0. Even more complicated formulas will give you a general solution to the \emph{quartic} equation, which has the form a x 4 + b x 3 + c x 2 + d x + e = 0. ax^4 + bx^3 + cx^2 + dx + e =0. ax4+bx3+cx2+dx+e=0. The formulas that give the solutions to the quadratic, cubic and quartic may look complicated, but they only involve a limited number of operations: addition, subtraction, multiplication and division, as well as taking square roots, cube roots, or fourth roots. The obvious question you might ask yourself now is whether we can find similar general formula for the quintic equation a x 5 + b x 4 + c x 3 + d x 2 + e x + f = 0 , ax^5 + bx^4 + cx^3 + dx^2 + ex + f =0, ax5+bx4+cx3+dx2+ex+f=0, or polynomial equations involving even higher powers of x x x.

Évariste Galois, drawn from memory by his brother in 1848, sixteen years after his death.
What we would like is a formula that gives a general solution and only involves addition, subtraction, multiplication and division, and taking roots. If an equation has such a formula giving a general solution, then we say it is solvable by radicals.
The result proved by Abel in 1824 is that there isn’t such a solution: the general quintic cannot be solved by radicals. This doesn’t mean that you can never solve a quintic. For example, the polynomial
x 5 − 1 = 0 x^5-1=0 x5−1=0 has a solution x = 1. x=1. x=1. But it does mean that there is not a nice, neat formula that gives the solution to the quintic in its most general form.
Abel proved the result, but it was Galois who a few years later provided real insight into why the quintic isn’t solvable by radicals. Galois is often credited with laying the foundation of group theory, the mathematical study of symmetry, with his work on equations. We usually think of symmetry as a visual thing: a picture, or a pattern might be symmetric. But what do symmetries have to do with equations? The answer is subtle, but beautiful.
Unchanging symmetry
First let’s think about what symmetry really is. We say that a square is symmetric because we can rotate it through multiples of 90 degrees, or reflect it in various axes, without changing its appearance. So symmetry is immunity to change: something is symmetric if you can perform a certain operation on it without changing it.
We can detect a hint of symmetry when we think about quadratic equations. As an example, the quadratic x 2 − 2 = 0 x^2-2 = 0 x2−2=0 has solutions x 1 = 2 x_1 = \sqrt{2} x1=2 and x 2 = − 2 . x_2 = -\sqrt{2}. x2=−2.
These are two distinct solutions, but in some intuitive sense they are very similar: one is just the negative of the other. Perhaps swapping these two solutions does not really make a difference. Just as a reflection, which does not make a difference to a square, is a symmetry, so swapping the solutions of the equation might also be a symmetry. But a symmetry of what?
Including irrationals

Like butterflies equations have symmetries too!
To understand this, let’s look at the numbers involved. The coefficients of our equation x 2 − 2 = 0 x^2-2 = 0 x2−2=0 are 1 and -2: these are nice and straight-forward \emph{rational numbers}. The solutions, however, are \emph{irrational numbers}: try as you might, you cannot write 2 \sqrt{2} 2 and − 2 -\sqrt{2} −2 as fractions. Most quadratic equations have solutions that are irrational numbers, so clearly when we think about them the collection of rational numbers is not enough. So let’s extend it. Instead of looking only at the set of rational numbers (for which we write Q {\mathbb Q} Q), let’s form a new set of numbers, which we will call Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2). It consists of all numbers that can be written in the form a + b 2 a+b\sqrt{2} a+b2, where a a a and b b b are rational numbers. This new collection contains all the rational numbers themselves (set b = 0 b=0 b=0) and also the two solutions 2 \sqrt{2} 2 and − 2 -\sqrt{2} −2 (set a = 0 a=0 a=0 and b = 1 b=1 b=1 or b = − 1 b=-1 b=−1). The new set Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) is nicely self-contained: you can add, subtract, multiply or divide any two numbers in Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) and the result will also be in Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2). Technically, Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) is what mathematicians call a \emph{field}. The self-contained nature under the operations of arithmetic is one of the properties of a field. It turns out that Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) is the smallest field that contains all the rational numbers and the solutions 2 \sqrt{2} 2 and − 2 -\sqrt{2} −2 to our equation.
Switching solutions
Now we can go back to our idea of swapping the two solutions 2 \sqrt{2} 2 and − 2 -\sqrt{2} −2 of the equation x 2 − 2 = 0 x^2-2=0 x2−2=0. Doing this to all numbers in the field Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) amounts to swapping a number a + b 2 a+b\sqrt{2} a+b2 with the number a − b 2 . a-b\sqrt{2}. a−b2. Let’s represent this swapping operation by a function f : f: f: f ( a + b 2 ) = a − b 2 . f(a+b\sqrt{2}) = a-b\sqrt{2}. f(a+b2)=a−b2. Applying f f f to all numbers in the field Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) does not really make a difference to Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) and its structure. It does not make any difference to the rational numbers in the field at all, as f ( a ) = f ( a + 0 × 2 ) = a − 0 × 2 = a . f(a) = f(a + 0\times \sqrt{2}) = a - 0\times \sqrt{2} = a. f(a)=f(a+0×2)=a−0×2=a. It does change the irrational numbers in the field, but once we have applied f f f to all of them, the overall collection of numbers is still exactly the same: it’s still Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2). (This is because if a + b 2 a+b\sqrt{2} a+b2 is a member of Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2), then so is a − b 2 . a-b\sqrt{2}. a−b2.) What is more, applying f f f to all members of Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) preserves the structure of addition, subtraction, multiplication and division. Suppose you add/subtract/multiply/divide two numbers a + b 2 a+b\sqrt{2} a+b2 and c + d 2 c+d\sqrt{2} c+d2 in Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) to get a third number e + f 2 e+f\sqrt{2} e+f2. Then adding/subtracting/multiplying/dividing f ( a + b 2 ) = a − b 2 f(a+b\sqrt{2}) = a-b\sqrt{2} f(a+b2)=a−b2 and f ( c + d 2 ) = c − d 2 f(c+d\sqrt{2}) = c-d\sqrt{2} f(c+d2)=c−d2 gives as the result f ( e + f 2 ) = e − f 2 f(e+f\sqrt{2}) = e-f\sqrt{2} f(e+f2)=e−f2 In this sense, the function f f f (which comes from swapping the two solutions) is a \emph{symmetry} associated to the equation x 2 − 2 = 0. x^2-2=0. x2−2=0. It does not make a difference to Q ( 2 ) . \mathbb{Q}(\sqrt{2}). Q(2). To give it its proper name, the function f f f is called a Q \mathbb{Q} Q-automorphism of the field Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2): it is a bijective function from Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) to itself, which leaves members of Q \mathbb{Q} Q unchanged and preserves the structure of the arithmetic operations.
Galois’ group
Are there any other Q \mathbb{Q} Q-automorphisms of Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2)? The answer is yes, there is one more, although it’s a boring one. It’s leaving every member of Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) unchanged. This is represented by the \emph{identity function} g ( x ) = x g(x) = x g(x)=x So the collection of Q \mathbb{Q} Q-automorphisms of Q ( 2 ) \mathbb{Q}(\sqrt{2}) Q(2) (that is, the collection of symmetries arising from x 2 − 2 = 0 x^2-2=0 x2−2=0) consist only of the functions g g g and f . f. f. The collection of symmetries of any object, whether it’s a shape like a square or an equation, forms a self-contained system called a \emph{group}. (A group is not dissimilar, though simpler, than a field.) The system is self-contained because when you follow one symmetry by another symmetry, the result is also a symmetry. In our example, following the symmetry ( Q \mathbb{Q} Q-automorphism) f f f by itself gets you back to where you started, so it amounts to performing the identity symmetry: f ( f ( a + b 2 ) ) = f ( a − b 2 ) = a + b 2 = g ( a + b 2 ) . f(f(a+b\sqrt{2})) = f(a-b\sqrt{2}) = a+b\sqrt{2}=g(a+b\sqrt{2}). f(f(a+b2))=f(a−b2)=a+b2=g(a+b2). Similarly, following f f f by g g g or g g g by f f f amounts to doing just f f f, and following g g g by g g g amounts to just doing g . g. g. The group of symmetries that comes from our equation, consisting of the two Q \mathbb{Q} Q-automorphisms g g g and f f f, is called the \emph{Galois group} of the equation x 2 − 2 = 0. x^2-2=0. x2−2=0.
Why you can’t solve the general quintic
We can do all of this for any other polynomial equation P P P, for example for a quintic of the form a x 5 + b x 4 + c x 3 + d x 2 + e x + f = 0 , ax^5 + bx^4 + cx^3 + dx^2 + ex + f =0, ax5+bx4+cx3+dx2+ex+f=0, where the coefficients a a a, b b b, c c c, d d d, e e e and f f f are rational numbers. Again you can extend the field of rational numbers, Q \mathbb{Q} Q, to form the smallest field (call it Q ( P ) \mathbb{Q}(P) Q(P)) that includes Q \mathbb{Q} Q and all the solutions to the equation P . P. P. This is called the \emph{splitting field} of P P P. Just as we did for the quadratic, you can look at the symmetries of this splitting field. These are Q \mathbb{Q} Q-automorphisms of Q ( P ) \mathbb{Q}(P) Q(P), which leave all the members of Q \mathbb{Q} Q unchanged, swap around the irrational members of Q ( P ) \mathbb{Q}(P) Q(P) and preserve the structure of addition, subtraction, multiplication and division. These form the Galois group of the equation P P P.

A French stamp celebrating Galois.
What Galois was able to show is that whether or not an equation is solvable by radicals depends on the structure of its Galois group. Sometimes the Galois group breaks up into smaller components that correspond to taking square roots, or cube roots, or n n nth roots for some larger n . n. n. If that is the case, then the equation is solvable by radicals. If, however, it doesn’t break up into smaller components in the right way, if you can’t disentangle the symmetries from each other, then you can’t find a general solution that involves only addition, subtraction, multiplication, division and taking roots — in that case you can’t solve the equation by radicals. It’s possible to show that there are quintic equations that don’t break up in the right way. These therefore aren’t solvable by radicals. And this means that we can’t find a general solution to the quintic as we have for the quadratic. The same is true for polynomial equations that involve higher powers of x x x too: there isn’t a general formula that solves them by radicals. The study of the solutions of equations using group theory is known as Galois theory, after its inventor.
You can read a more detailed, but still accessible, account of this on our sister site NRICH.
via:
-
Stubborn equations and the study of symmetry
你真的会解方程吗?
中国物理学会期刊网 2021 年 05 月 24 日
你真的会解方程吗?今天我们从简单的解方程开始,为大家介绍一位英年早逝的数学家的工作,从这些工作中我们将看到优美的对称性,以及蕴含在其中的和谐奥妙。

尼尔斯・亨里克・阿贝尔
1824 年,一位年轻的挪威数学家尼尔斯・亨里克・阿贝尔取得了一个与某类方程相关的令人震惊的结果。不久之后,法国天才数学家埃瓦里斯特・伽罗瓦以深入的眼光证明了这一结果为什么是正确的 —— 并在这个过程中开创了用数学研究对称性的先河。可惜两人都英年早逝,没有来得及享受他们的工作带来的好处。阿贝尔于 1829 年死于肺结核和贫困,时年 26 岁。伽罗瓦死于 1832 年,他在一场据称是为了争夺一个女人而进行的决斗中被杀死。当时他只有二十岁。
那么他们做出了什么样的工作?方程和对称性又有什么关系?
解方程
Solving Equations
最著名的公式之一是二次方程的通解公式,如果方程写为:
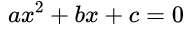
那么通解公式就可以告诉我们方程的解为:
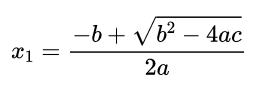
以及
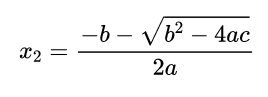
无论 a,b,c 的值是多少,这个公式都可以告诉你解是多少。它们使用起来很方便。
这有一个类似的但复杂得多的公式可以告诉你三次方程的通解,方程的形式为:
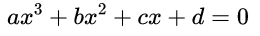
还有一些更复杂的方程可以告诉你四次方程的通解,这些方程可以写为:
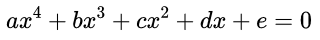
虽然关于二次,三次,四次方程的通解公式看起来有些复杂,但是它们只包含了有限个运算操作:加、减、乘、除、开平方、开三次方、开四次方。
很显然,你接下来会问,我们可以为五次方程找到一个类似的通解公式吗?
更一般的,包含 x 高阶项的多项式方程的通解公式长什么样子?

伽罗瓦画像 在他死后 16 年的 1848 年,由他的兄弟根据记忆所作
我们想要的是一个公式,这个公式只包含加减乘除和求根操作。如果一个方程具有这样一个通解公式,那么我们说这个方程是有根式解的。
1824 年阿贝尔证明的结论是:对于一般的五次方程,不存在根式解。当然,这并不意味所有的五次方程都是没有根式解的。例如,多项式方程:
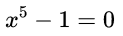
拥有一个解: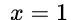 。
。
但是对于一般的五次方程,确实不存在一个普适的根式解公式。
阿贝尔证明了这一结果,但几年后,伽罗瓦才真正意识到为什么五次方程不存在根式解。伽罗瓦常被认为群论的奠基人,群论是一门研究对称性的数学。 我们通常认为对称性是一种视觉现象:一幅画或图案可能是对称的。但是对称性和方程有什么关系呢?答案有些微妙,但非常美丽。
不变的对称性
Unchanging Symmetry
首先,让我们思考对称性真正的含义。我们说一个正方形是对称的是因为我们将它绕着中心轴旋转 90 度,或者将它对于各种轴做反射操作并不会改变它的外观。所以对称性意味着没有变化:如果我们对某个物体进行某种操作之后并没有改变它,那么它就具有对称性。
当我们思考二次方程式,我们可以发现少许对称性。例如,二次方程
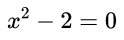
拥有两个解

方程具有两个离散的解,但是某种意义上,它们非常相似:只需在一个解上加上一个负号就可以得到另一个解。也许交换两个解并不会带来什么不同,就像对正方形做镜像操作一样意味着一种对称性一样,交换方程的两个解也许也意味着某种对称性。但究竟是哪种对称性呢?
加入无理数
Including Irrationals

蝴蝶有对称性,方程也有对称性!
为了理解这些结果,让我们考察一下方程所包含的数字:
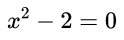
方程的系数是 1 和 - 2:两个系数都是有理数。但是它的解却是两个无理数:
方程的系数是 1和 -2:两个系数都是有理数。但是它的解却是两个无理数:你无法将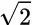 和
和 写成两个整数相除的形式。多数二次方程的解都是无理数,因此只考虑方程的系数是不够的。
写成两个整数相除的形式。多数二次方程的解都是无理数,因此只考虑方程的系数是不够的。
让我们把视野放宽一点,不光考察一组有理数(写作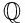 ),我们还要考察一组新的数,这组数写作
),我们还要考察一组新的数,这组数写作 。这组数包含所有可以写作
。这组数包含所有可以写作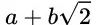 的数,其中 a 和 b 是有理数。很显然,新的一组数包含所有的有理数(b=0),同时也包含前面二次方程的两个解
的数,其中 a 和 b 是有理数。很显然,新的一组数包含所有的有理数(b=0),同时也包含前面二次方程的两个解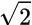 和
和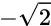 。
。
新的一组数是自包含的( self-contained):你可以将其中的两个数相加、相减、乘或者相除,得到的结果仍然在这组数里。在数学中, 被称为一个域(field)。在代数操作下的自包含性是域的基本特性。事实上,
被称为一个域(field)。在代数操作下的自包含性是域的基本特性。事实上, 是包含所有有理数以及
是包含所有有理数以及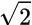 和
和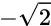 的最小的域。
的最小的域。
交换两个解
Switching Solutions
现在我们回到将两个解 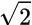 和
和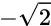 进行交换的想法。在
进行交换的想法。在 中将所有的
中将所有的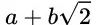 和
和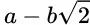 进行交换,我们可以用函数 f 来表示这种交换操作:
进行交换,我们可以用函数 f 来表示这种交换操作:
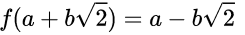
将 f 作用在 中的所有数上并不会改变
中的所有数上并不会改变 也不会改变它的结构。并且,它并不会改变这个域中的所有有理数。
也不会改变它的结构。并且,它并不会改变这个域中的所有有理数。
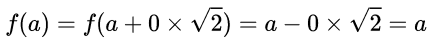
很显然,f 并不改变域中的有理数,对于无理数,经 f 作用后仍然处于 中。(因为
中。(因为 是
是 中的一个数,
中的一个数,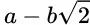 也是
也是 中的一个数)
中的一个数)
更进一步,将 f 作用在 上保持加减乘除的结构。假设你对
上保持加减乘除的结构。假设你对 中的两个数
中的两个数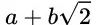 和
和 进行加、减、乘、除操作得到新的数
进行加、减、乘、除操作得到新的数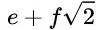 ,然后将
,然后将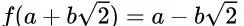 和
和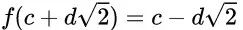 进行加、减、乘、除可以得到
进行加、减、乘、除可以得到 。
。
在某种意义上,函数 f 是方程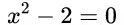 的一个对称变换。它不会改变
的一个对称变换。它不会改变 。函数 f 被称为域
。函数 f 被称为域 的
的 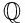 - 自同构:它是从
- 自同构:它是从 到自身的双射函数,它不改变
到自身的双射函数,它不改变 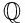 中的数并且保持
中的数并且保持 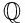 在代数操作下的结构。
在代数操作下的结构。
伽罗瓦群
Galois’s Group
 还有其它的
还有其它的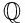 - 自同构变换吗?答案是肯定的,其实还有一个
- 自同构变换吗?答案是肯定的,其实还有一个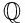 - 自同构变换,尽管这个自同构变换很平庸。它使
- 自同构变换,尽管这个自同构变换很平庸。它使 中的每个数保持不变。用函数表示就是:
中的每个数保持不变。用函数表示就是: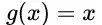 。
。 的
的 - 自同构集合(也就是方程的对称性的集合)只包含 g 和 f 两个元素。
- 自同构集合(也就是方程的对称性的集合)只包含 g 和 f 两个元素。
一个事物,无论它是一个图形还是一个方程,它的对称性的集合构成一个群。这个系统是自包含的原因是两个对称变换的组合仍然构成一个对称变换。在我们的例子中,将对称变换 f 连续两次作用在一个数上不会改变这个数:
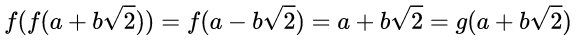
类似的,先作用 f 后作用 g,或者先作用 g 后作用 f 的组合构成了 f,而 g 和 g 的组合仍然是 g。我们的方程的对称性构成的群包含两个 - 自同构 g 和 f,它被称为方程
- 自同构 g 和 f,它被称为方程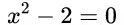 的伽罗瓦群。
的伽罗瓦群。
为什么你解不出一般的五次方程?
Why you can’t solve the general quintic?
我们可以对其他任意多项式做类似的事情,例如对一个五次方程:

A,b,c,d,e 和 f 是有理数。同样的,我们可以将有理数域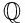 扩展成包含
扩展成包含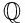 和
和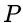 方程的解的最小的域
方程的解的最小的域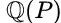 。它被称为
。它被称为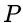 的分裂域(splitting field)
的分裂域(splitting field)
就像我们对二次方程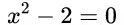 做的那样,你可以观察一下这个分裂域的对称性。它的
做的那样,你可以观察一下这个分裂域的对称性。它的 - 自同构包含不改变域内数字的自同构变换和不改变域的结构的自同构变换,它们构成
- 自同构包含不改变域内数字的自同构变换和不改变域的结构的自同构变换,它们构成 的伽罗瓦群。
的伽罗瓦群。

纪念伽罗瓦的法国邮票
伽罗瓦所能证明的是,一个方程是否有根式解,取决于它的伽罗瓦群的结构。有时候伽罗瓦群可以被分成更小的分量,它们和取 n 次方根有关。如果是这种情况,那么方程拥有根式解。
然而,如果它无法以恰当的方式分被解成更小的分量,如果你不能把对称性分离出来,那么你就找不到一个只涉及加、减、乘、除和求根的通解,在这种情况下,方程不存在根式解。
我们可以证明,五次方程并不能以恰当的方式分解。因此,五次方程不存在根式通解。对于包含 x 的更高次幂的多项式方程也是一样的:它们没有根式通解。用群论研究方程的解被称为伽罗瓦理论,这一理论以其发明者的名字命名。
作者:Marianne Freiberger
翻译:Nothing
审校:C&C
via:
-
你真的会解方程吗?Marianne 中国物理学会期刊网 2021 年 05 月 24 日 10:00 北京






















 3055
3055

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








