MATLAB Coder 应用：转换 MATLAB 代码至 C/C++ | 实践步骤与问题解决

已于 2025-04-23 11:36:52 修改
阅读量900 收藏 27
点赞数 13
分类专栏： clean code 文章标签： Matlab C/C++
于 2025-04-22 17:57:19 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/u013669912/article/details/142526671
版权

注：本文为 “ MATLAB 代码至 C/C++ 应用” 相关文章合辑。

未整理去重。
如有内容异常，请看原文。

MATLAB 代码转换为 C/C++ 代码的详细指南

随心 390 @zhihu 发布于 2020-07-12 12:39

在实际项目中，我们常常遇到需要将 MATLAB 代码转换为 C/C++ 代码的情况。例如，项目主体部分用 C++ 编写，但其中部分算法用 MATLAB 实现。此时，MATLAB Coder 提供了一种高效的解决方案。

img

本文将详细介绍如何使用 MATLAB Coder 将 MATLAB 代码转换为 C/C++ 代码，并指出一些常见的“雷区”。

1. 准备工作

在使用 MATLAB Coder 之前，需要对 MATLAB 代码进行以下处理：

  1. 删除注释：MATLAB 代码中的所有注释必须删除，否则无法成功转换。这是第一个“雷区”。

  2. 删除画图和打印部分的代码：包括 plot、disp 等函数的调用。这些代码会导致转换失败，是第二个“雷区”。

  3. 处理动态矩阵分配：在 MATLAB 中，可以使用如下代码动态添加数据到矩阵中：

A = []; % 初始化矩阵 A 为空
A = [A; B]; % 将矩阵 B 添加到矩阵 A 的下方

然而，C/C++ 不支持这种动态分配方式。解决方案是先计算需要添加的行数 ( m ) 和列数 ( n )，然后初始化矩阵 ( A )，并通过循环添加数据：

A = zeros(1, n);
count = 1;
for i = 1:m
    A(count, :) = B;
    count = count + 1;
end

2. 封装主函数

MATLAB Coder 要求主函数是一个有明确输入和输出的函数，而不是脚本函数。以遗传算法（GA）求解旅行商问题（TSP）为例，原始主函数如下：

% 输入数据
x = [38.24, 39.57, 40.56, 36.26, 33.48, 37.56, 38.42, 37.52, 41.23, 41.17, 36.08, 38.47, 38.15, 37.51, 35.49, 39.36, 38.09, 36.09, 40.44, 40.33, 40.37, 37.57];
y = [20.42, 26.15, 25.32, 23.12, 10.54, 12.19, 13.11, 20.44, 9.100, 13.05, -5.210, 15.13, 15.35, 15.17, 14.32, 19.56, 24.36, 23, 13.57, 14.15, 14.23, 22.56];
vertexs = [x; y]';
n = length(x); % 城市数目
h = pdist(vertexs);
dist = squareform(h); % 距离矩阵
% 遗传算法参数设置
NIND = 50; % 种群大小
MAXGEN = 1000; % 迭代次数
Pc = 0.8; % 交叉概率
Pm = 0.2; % 变异概率
pSwap = 0.2; % 选择交换结构的概率
pReversion = 0.5; % 选择逆转结构的概率
pInsertion = 1 - pSwap - pReversion; % 选择插入结构的概率
N = n; % 染色体长度 = 城市数目
% 种群初始化
Chrom = InitPop(NIND, N);
% 优化
gen = 1; % 计数器
bestChrom = Chrom(1, :); % 初始全局最优个体
bestL = RouteLength(bestChrom, dist); % 初始全局最优个体的总距离
BestChrom = zeros(MAXGEN, N); % 记录每次迭代过程中全局最优个体
BestL = zeros(MAXGEN, 1); % 记录每次迭代过程中全局最优个体的总距离
while gen <= MAXGEN
    % 二元锦标赛选择
    SelCh = BinaryTourment_Select(Chrom, dist);
    % OX 交叉
    SelCh = Recombin(SelCh, Pc);
    % 变异
    SelCh = Mutate(SelCh, Pm, pSwap, pReversion, pInsertion);
    % 将 Chrom 更新为 SelCh
    Chrom = SelCh;
    % 计算当前代所有个体总距离
    Obj = ObjFunction(Chrom, dist);
    % 找出当前代中最优个体
    [minObj, minIndex] = min(Obj);
    % 将当前代中最优个体与全局最优个体进行比较，如果当前代最优个体更好，则将全局最优个体进行替换
    if minObj <= bestL
        bestChrom = Chrom(minIndex, :);
        bestL = minObj;
    end
    % 记录每一代全局最优个体，及其总距离
    BestChrom(gen, :) = bestChrom;
    BestL(gen, :) = bestL;
    % 显示外层循环每次迭代的信全局最优路线的总距离
    disp(['第' num2str(gen) '次迭代：全局最优路线总距离 = ' num2str(bestL)]);
    % 画出每次迭代的全局最优路线图
    figure(1);
    PlotRoute(bestChrom, x, y);
    pause(0.01);
    % 计数器加 1
    gen = gen + 1;
end
% 打印每次迭代的全局最优个体的总距离变化趋势图
figure;
plot(BestL, 'LineWidth', 1);
title('优化过程');
xlabel('迭代次数');
ylabel('总距离');

封装后的主函数如下：

% 输入 x, y：城市的 x, y 坐标
% 输入 NIND：种群大小
% 输入 MAXGEN：迭代次数
% 输入 Pc：交叉概率
% 输入 Pm：变异概率
% 输入 pSwap：选择交换结构的概率
% 输入 pReversion：选择逆转结构的概率
% 输入 pInsertion：选择插入结构的概率
% 输出 bestChrom：全局最优个体
function bestChrom = GA_TSP(x, y, NIND, MAXGEN, Pc, Pm, pSwap, pReversion, pInsertion)
% 输入数据
vertexs = [x; y]';
n = length(x); % 城市数目
h = pdist(vertexs);
dist = squareform(h); % 距离矩阵
N = n; % 染色体长度 = 城市数目
% 种群初始化
Chrom = InitPop(NIND, N);
% 优化
gen = 1; % 计数器
bestChrom = Chrom(1, :); % 初始全局最优个体
bestL = RouteLength(bestChrom, dist); % 初始全局最优个体的总距离
BestChrom = zeros(MAXGEN, N); % 记录每次迭代过程中全局最优个体
BestL = zeros(MAXGEN, 1); % 记录每次迭代过程中全局最优个体的总距离
while gen <= MAXGEN
    % 二元锦标赛选择
    SelCh = BinaryTourment_Select(Chrom, dist);
    % OX 交叉
    SelCh = Recombin(SelCh, Pc);
    % 变异
    SelCh = Mutate(SelCh, Pm, pSwap, pReversion, pInsertion);
    % 将 Chrom 更新为 SelCh
    Chrom = SelCh;
    % 计算当前代所有个体总距离
    Obj = ObjFunction(Chrom, dist);
    % 找出当前代中最优个体
    [minObj, minIndex] = min(Obj);
    % 将当前代中最优个体与全局最优个体进行比较，如果当前代最优个体更好，则将全局最优个体进行替换
    if minObj <= bestL
        bestChrom = Chrom(minIndex, :);
        bestL = minObj;
    end
    % 记录每一代全局最优个体，及其总距离
    BestChrom(gen, :) = bestChrom;
    BestL(gen, :) = bestL;
    % 显示外层循环每次迭代的信全局最优路线的总距离
    disp(['第' num2str(gen) '次迭代：全局最优路线总距离 = ' num2str(bestL)]);
    % 画出每次迭代的全局最优路线图
    figure(1);
    PlotRoute(bestChrom, x, y);
    pause(0.01);
    % 计数器加 1
    gen = gen + 1;
end
% 打印每次迭代的全局最优个体的总距离变化趋势图
figure;
plot(BestL, 'LineWidth', 1);
title('优化过程');
xlabel('迭代次数');
ylabel('总距离');
end

3. 新建一个脚本函数

封装主函数后，删除原来的脚本函数 GA_TSP，新建一个脚本函数 TEST，在其中提供封装后的主函数的输入数据：

clear;
clc;
x = [38.24, 39.57, 40.56, 36.26, 33.48, 37.56, 38.42, 37.52, 41.23, 41.17, 36.08, 38.47, 38.15, 37.51, 35.49, 39.36, 38.09, 36.09, 40.44, 40.33, 40.37, 37.57];
y = [20.42, 26.15, 25.32, 23.12, 10.54, 12.19, 13.11, 20.44, 9.100, 13.05, -5.210, 15.13, 15.35, 15.17, 14.32, 19.56, 24.36, 23, 13.57, 14.15, 14.23, 22.56];
NIND = 50;
MAXGEN = 1000;
Pc = 0.8;
Pm = 0.2;
pSwap = 0.2;
pReversion = 0.5;
pInsertion = 1 - pSwap - pReversion;
bestChrom = GA_TSP(x, y, NIND, MAXGEN, Pc, Pm, pSwap, pReversion, pInsertion);

4. 开始转换

4.1 点击 MATLAB Coder

img

4.2 添加封装后的 GA_TSP 函数

img

img

img

4.3 根据提示修改代码

在转换过程中，可能会遇到一些问题。例如，OX 函数需要进行修改。修改后的 OX 函数如下：

function [a0, b0] = OX(a, b)
L = length(a);
while 1
    r = randi([1, L], 1, 2);
    r1 = r(1);
    r2 = r(2);
    if r1 ~= r2
        s = min([r1, r2]);
        e = max([r1, r2]);
        a0 = zeros(1, L + e - s + 1);
        b0 = zeros(1, L + e - s + 1);
        a0(1:e - s + 1) = b(s:e);
        a0(e - s + 2:L + e - s + 1) = a;
        b0(1:e - s + 1) = a(s:e);
        b0(e - s + 2:L + e - s + 1) = b;
        for i = 1:length(a0)
            aindex = find(a0 == a0(i));
            bindex = find(b0 == b0(i));
            if length(aindex) > 1
                a0(aindex(2)) = [];
            end
            if length(bindex) > 1
                b0(bindex(2)) = [];
            end
            if i == length(a)
                break
            end
        end
        break
    end
end

4.4 定义输入变量类型

img

img

img

img

4.5 检验运行环境

在检验运行环境时，可能会遇到新的报错。例如，Mutate 函数需要进行修改。修改后的 Mutate 函数如下：

function SelCh = Mutate(SelCh, Pm, pSwap, pReversion, pInsertion)
NSel = size(SelCh, 1);
for i = 1:NSel
    if Pm >= rand
        index = Roulette(pSwap, pReversion, pInsertion);
        route1 = SelCh(i, :);
        flag = zeros(1, 3);
        flag(1) = index == 1;
        flag(2) = index == 2;
        flag(3) = index == 3;
        if flag(1)
            route2 = Swap(route1);
        elseif flag(2)
            route2 = Reversion(route1);
        else
            route2 = Insertion(route1);
        end
        SelCh(i, :) = route2;
    end
end

4.6 生成 C 代码

完成上述步骤后，点击 Generate 生成 C 代码。生成的 C 代码位于 MATLAB 代码文件夹下的 codegen 文件夹中，具体路径为：

codegen 文件夹 -> lib 文件夹 -> GA_TSP 文件夹

img

img

img

至此，使用 MATLAB Coder 成功将遗传算法（GA）求解旅行商问题（TSP）的 MATLAB 代码转换为 C 代码。

如何将 MATLAB 代码生成为 C/C++ 代码？

蚕与禅 已于 2024-05-11 16:41:55 修改

在 C/C++ 软件开发中，若部分核心算法用 MATLAB 编写，但不想逐行翻译，则可以使用 MATLAB 自带的 coder 命令进行代码自动翻译，以达到省时省力的目的。以下是详细步骤：

1. 封装 MATLAB 代码为函数：

img

img

function [aglA, aglB, aglC] = CalAglOfTriangle(a, b, c)
aglA = acosd((b^2 + c^2 - a^2) / (2 * b * c));
aglB = acosd((c^2 + a^2 - b^2) / (2 * c * a));
aglC = acosd((a^2 + b^2 - c^2) / (2 * a * b));
end

2. 新建一个 Test.m 脚本，调用封装的函数：

img

clear all;
aLine = 36371;
bLine = 6371;
cLine = 34197.667473781417;
[aglA, aglB, aglC] = CalAglOfTriangle(aLine, bLine, cLine);

3. 运行测试脚本，查看输出结果。

img

4. 在命令窗口输入 coder

5. 选择要转换的函数：

img

可以看到 .prj 工程所在的绝对路径，根据需要选择数值转换方式（通常使用默认方式）。

  1. 点击“Next”。

  2. 选择调用函数的脚本：

    img

  3. 点击“自动定义输入类型”按钮：

    img

    注意：这里是三个 double 型，根据实际需求可以点击修改。

  4. 点击“Next”。

  5. 点击“检查问题”按钮：

    img

    绿色对勾表示未检测到问题。若检测到问题，应根据提示进行处理。

  6. 点击“Next”。

  7. 选择要生成的语言（C 或 C++），点击“生成”：

    img

  8. 稍等片刻，出现如下界面：

    img

  9. 点击“Next”。

至此，转换成功！在提示的路径下可以找到转换后的代码以及示例。

  1. 找到对应的 .h 和 .cpp 文件：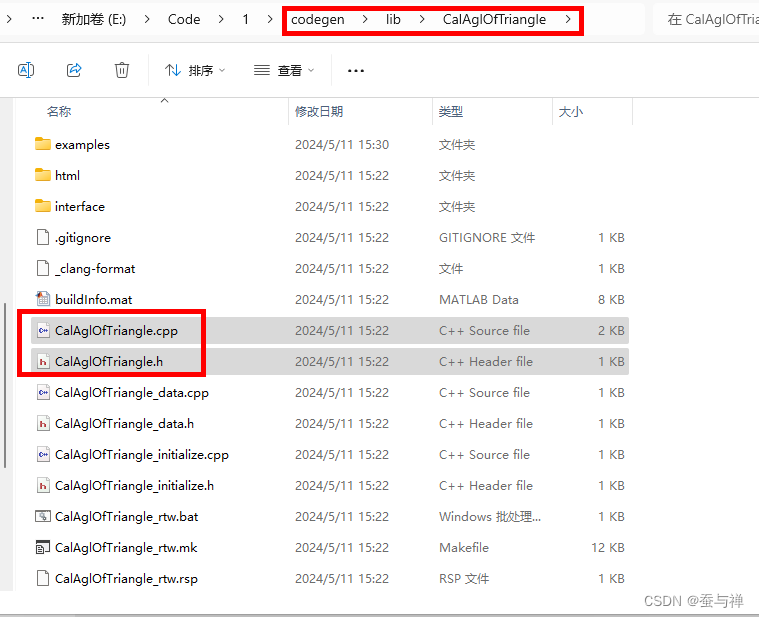

    img

  2. 在 Visual Studio 中新建控制台工程，并将上述 .h 和 .cpp 文件添加到工程中：

    img

    img

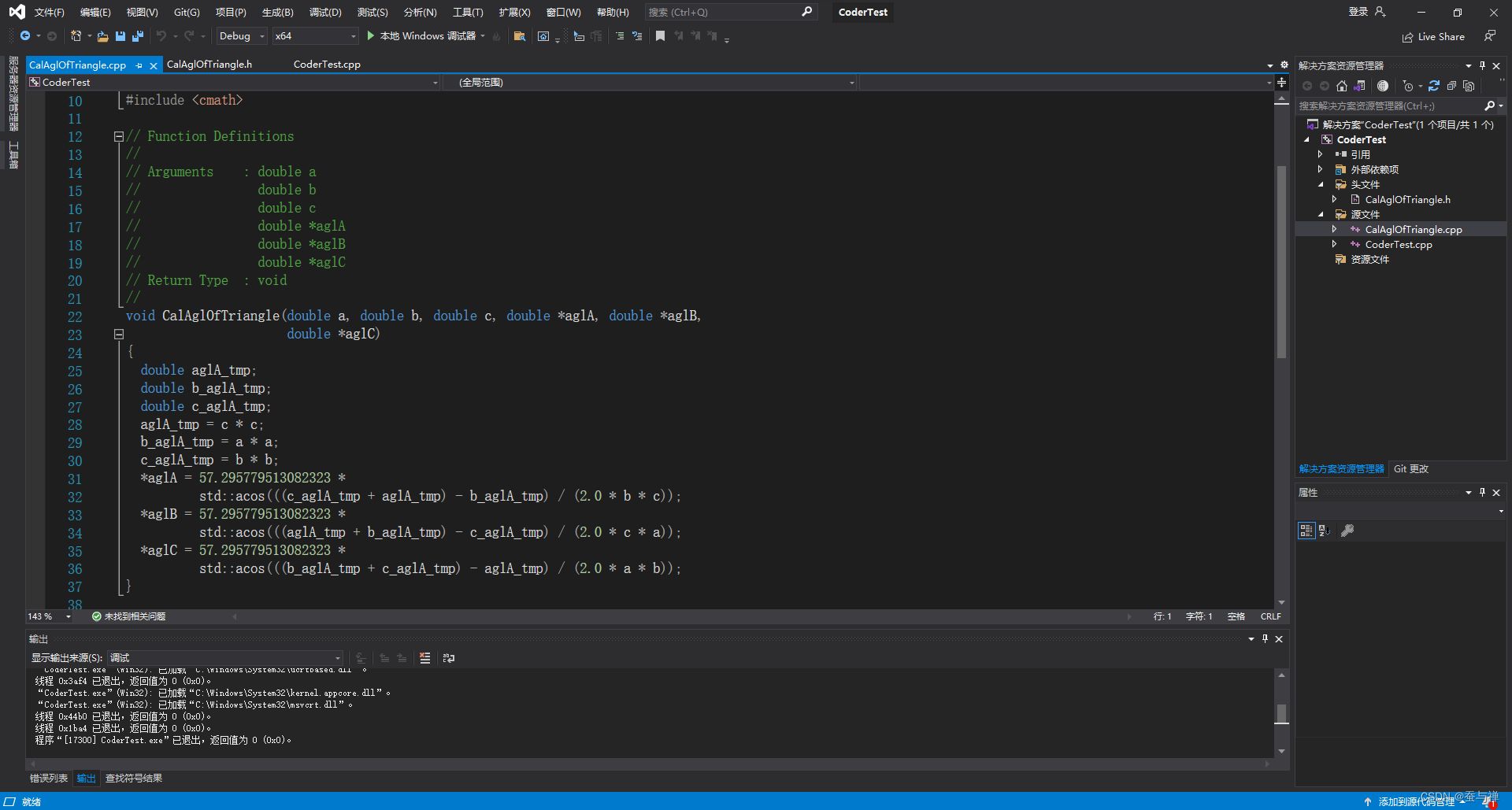
  3. 根据编译报错提示，补充缺失的文件：

    img

  4. 在 main 函数中调用自动生成的函数，运行结果正确：

    img

总结：本文演示的是一个简单的 MATLAB 函数（根据三角形三条边计算三个夹角）。实际的 MATLAB 代码或函数可能比较复杂，在根据 coder 命令提示进行问题检测时可能会遇到各种报错提示。此时无需慌张，静下心来分析，大部分报错都是可以屏蔽或修改的。笔者曾将十几个复杂的 MATLAB 函数整合封装为一个 C++ 类，删除多余的头文件后，最终只剩下一个 .h 和 .cpp 文件。

使用 MATLAB Coder Generation 将 m 语言转化为 C++ 过程中遇到的问题及解决

在使用 MATLAB Coder 时，可能会遇到一些问题。以下是一些常见问题及其解决方案：

一、MATLAB Coder 的使用步骤

在命令行窗口输入以下命令启动 MATLAB Coder：

>> coder

img

img

建议在定义（一维）变量数组的数据类型及大小时，定义为 double (1 × :inf)，避免在数组运算过程中由于引入新的中间变量数组，导致数组计算的等式左右两端数组大小不对等。

img

下一步：

img

img

②：在点击“Generate”后，可能会遇到许多报错，需要根据提示修改 .m 文件代码。

二、遇到的问题及解决方案

1. cell2mat 和 quadprog 函数不支持代码生成

以自定义的 MPC 函数为例，其中调用了 quadprog 函数求解：

% 新的 A, B, C 矩阵
A_cell = cell(2, 2);
B_cell = cell(2, 1);
A_cell{1, 1} = a;
A_cell{1, 2} = b;
A_cell{2, 1} = zeros(Nu, Nx);
A_cell{2, 2} = eye(Nu);
B_cell{1, 1} = b;
B_cell{2, 1} = eye(Nu);
A = cell2mat(A_cell);
B = cell2mat(B_cell);
C = [eye(Nx), zeros(Nx, Nu)];
% PHI 矩阵及 THETA 矩阵
PHI_cell = cell(Np, 1);
THETA_cell = cell(Np, Nc);
for j = 1:1:Np
    PHI_cell{j, 1} = C * A^j; % cell 的引用必须用大括号 {}，否则被看做 double 类型
    for k = 1:1:Nc
        if k <= j
            THETA_cell{j, k} = C * A^(j - k) * B; % 左下角矩阵填充
        else
            THETA_cell{j, k} = zeros(Nx, Nu); % 矩阵左上角均为 0
        end
    end
end
PHI = cell2mat(PHI_cell); % size(PHI) = [Nx * Np, Nx + Nu]
THETA = cell2mat(THETA_cell); % size(THETA) = [Nx * Np, Nu * (Nc + 1)]
% 二次型目标函数的相关矩阵
H_cell = cell(2, 2);
H_cell{1, 1} = THETA' * Q * THETA + R;
H_cell{1, 2} = zeros(Nu * Nc, 1);
H_cell{2, 1} = zeros(1, Nu * Nc);
H_cell{2, 2} = row; % row 松弛因子，为了能够得到最优解，防止出现无解的情况
H = cell2mat(H_cell);
% 误差 E 矩阵
E = PHI * kesi; % 预测时域内的跟踪误差
% g 矩阵
g_cell = cell(1, 2);
g_cell{1, 1} = 2 * E' * Q * THETA;
g_cell{1, 2} = 0;
g = cell2mat(g_cell);
% 约束条件的相关矩阵
% A_I 矩阵
A_t = zeros(Nc, Nc); % 下三角矩阵
for p = 1:1:Nc
    for q = 1:1:Nc
        if q <= p
            A_t(p, q) = 1;
        else
            A_t(p, q) = 0;
        end
    end
end
A_I = kron(A_t, eye(Nu));
% Ut 矩阵
Ut = kron(ones(Nc, 1), U);
% 控制量和控制量变化量的约束
Umin = kron(ones(Nc, 1), u_min);
Umax = kron(ones(Nc, 1), u_max);
delta_Umin = kron(ones(Nc, 1), delta_min);
delta_Umax = kron(ones(Nc, 1), delta_max);
% 用于 quadprog 函数不等式约束 Ax <= b 的矩阵 A 和向量 b
A_cons_cell = {A_I zeros(Nu * Nc, 1); -A_I zeros(Nu * Nc, 1)}; % 为了和 H 的列数匹配，新添加一列 0
b_cons_cell = {Umax - Ut; -Umin + Ut};
A_cons = cell2mat(A_cons_cell);
b_cons = cell2mat(b_cons_cell);
% △U 的上下边界
lb = [delta_Umin; 0]; % (求解方程) 状态量下界，包含控制时域内控制增量和松弛因子
ub = [delta_Umax; 10]; % (求解方程) 状态量上界，包含控制时域内控制增量和松弛因子
% 开始求解过程
options = optimset('Algorithm', 'interior-point-convex');
% ↑内点法求解二次规划问题
delta_U = quadprog(H, g, A_cons, b_cons, [], [], lb, ub, [], options);

问题：编译代码时遇到“cell2mat 及 quadprog optimset is not supported for code generation”的问题。这是因为 MATLAB 自己封装的函数不支持 C++ 代码生成，需要将其定义为外部函数，即使用 coder.extrinsic 声明。

解决方案：

  1. 将 cell2mat 替换为固定大小的矩阵分配方式。

  2. 将 quadprog 和 optimset 声明为外部函数：

    coder.extrinsic('optimoptions');
coder.extrinsic('quadprog');

    并将 optimset 替换为 optimoptions：

    options = optimoptions('quadprog', 'Algorithm', 'interior-point-convex');

2. mxArray 类型变量的使用问题

问题：编译代码时遇到“Expected either a logical, char, int, fi, single, or double. Found an mxArray. MxArrays are returned from calls to the MATLAB interpreter and are not supported inside expressions. They may only be used on the right-hand side of assignments and as arguments to extrinsic functions.”

解决方案：

在 MATLAB 中，mxArray 是 MATLAB 解释器返回的数据类型，它不能直接用于表达式计算，只能用于赋值操作和作为外部函数的参数。因此，需要初始化被赋为 mxArray 的变量，将其转换为 double 类型，以便进行后续运算。

例如，对于变量 delta_U，可以进行如下初始化：

delta_U = zeros(size(lb)); % 初始化 delta_U 为与 lb 相同大小的零矩阵

这样，系统会将其识别为 double 类型，从而可以进行后续的运算。

3. cell2mat 和 quadprog 不能被生成 C++

问题：在代码生成过程中，cell2mat 和 quadprog 函数无法直接生成 C++ 代码。

解决方案：

  1. 替换 cell2mat：将所有 cell 类型的矩阵转换为固定大小的矩阵。例如，将以下代码：

    A = cell2mat(A_cell);
B = cell2mat(B_cell);
PHI = cell2mat(PHI_cell);
THETA = cell2mat(THETA_cell);
H = cell2mat(H_cell);
g = cell2mat(g_cell);
A_cons = cell2mat(A_cons_cell);
b_cons = cell2mat(b_cons_cell);

    替换为固定大小的矩阵分配方式：

    A = zeros(5); % 假设 A 的大小为 5x5
B = zeros(5, 2); % 假设 B 的大小为 5x2
PHI = zeros(Np * Nx, 5); % 假设 PHI 的大小为 Np*Nx x 5
THETA = zeros(Np * Nx, Nc * Nu); % 假设 THETA 的大小为 Np*Nx x Nc*Nu
H = zeros(61); % 假设 H 的大小为 61x61
g = zeros(1, 61); % 假设 g 的大小为 1x61
A_cons = zeros(Nu * Nc * 2, Nu * Nc + 1); % 假设 A_cons 的大小为 Nu*Nc*2 x (Nu*Nc+1)
b_cons = zeros(Nu * Nc * 2, 1); % 假设 b_cons 的大小为 Nu*Nc*2 x 1

  2. 处理 quadprog：由于 quadprog 函数不支持代码生成，可以将其声明为外部函数，并在生成的 C++ 代码中手动实现其功能。例如：

    coder.extrinsic('quadprog');
delta_U = quadprog(H, g, A_cons, b_cons, [], [], lb, ub, [], options);

    在生成的 C++ 代码中，可以使用第三方库（如 Eigen 或 Ceres Solver）来实现二次规划求解器的功能。

三、MATLAB 版本问题

问题：在 MATLAB 和 Visual Studio 版本不匹配时，可能会遇到代码生成失败的问题。例如，使用 MATLAB 2019 和 Visual Studio 2019 时，可能会遇到以下错误：

??? The extrinsic function 'ce112mat' is not available for standalone code generation.

解决方案：

  1. 升级 MATLAB 版本：建议使用更高版本的 MATLAB（例如 MATLAB 2022a 或更高版本）。高版本的 MATLAB 对代码生成的支持更好，同时也能更好地兼容 Visual Studio 的新版本。

  2. 配置 MATLAB 和 Visual Studio 的环境：确保 MATLAB 和 Visual Studio 的版本兼容。可以通过以下命令在 MATLAB 中配置编译器：

    >> mex -setup C++

    如果配置成功，会显示类似以下信息：

    “找到已安装的编译器 'Microsoft Visual C++ 2019 (C)'。
MEX 配置为使用 'Microsoft Visual C++ 2019 (C)' 以进行 C 语言编译。”

四、MATLAB 转 C/C++ 常见问题总结

  1. 使用变量前声明变量：在 MATLAB 中可以容忍未声明的变量，但在 C/C++ 中必须提前声明变量并分配内存。

    tmp = zeros(6, 6); % 预分配内存
for i = 1:6
    tmp(:, i) = ones(6, 1);
end

  2. 避免内联嵌套 scripts：MATLAB 转 C/C++ 不支持内联嵌套 scripts。可以将嵌套的 scripts 内联到主函数中，或者将其写成无参函数调用。

  3. 避免离开变量作用域后使用变量：在 MATLAB 中，变量可以在离开其作用域后继续使用，但在 C/C++ 中这是不允许的。

  4. 避免动态分配内存语法：MATLAB 中的动态数组分配语法（如 array = [array, i]）在 C/C++ 中不支持。可以使用预分配内存的方式替代。

  5. 避免使用 load 和高级函数：load 和一些高级函数（如 care、fsolve 等）不支持代码生成。如果需要使用这些函数，可以考虑从底层实现。

  6. 确保函数返回值有逻辑值：在 MATLAB 中，函数的返回值必须在所有逻辑分支中都有赋值。

  7. 尽量少用 global：虽然 MATLAB 转 C/C++ 支持 global，但建议尽量避免使用，以提高代码的可读性和封装性。

  8. 注释掉无关代码：在转换代码时，建议注释掉与业务逻辑无关的代码，如画图和打印代码。

总结

“尽量用底层语言的编程思维来写 MATLAB”。通过遵循上述建议，可以有效减少 MATLAB 代码转换为 C/C++ 代码时的错误，提高代码的可移植性和可维护性。

利用硬件加速大规模科学计算 | 从 MATLAB 到 C/C++ 代码

作者 周拥华、MathWorks
2022 年发布

无论是传统的系统仿真还是如今火热的人工智能，都涉及到大量的科学计算，高手们也许对利用多处理器、集群和 GPU 的编程技术驾轻就熟，但对初学者而言怎么样利用硬件来加速大规模科学计算无疑是个门槛较高的问题。作者试图用这篇简单的文章，帮助初学者了解，从 MATLAB 到 C/C++ 代码，可供使用的一些简单快捷的选项，算是入门吧。

利用硬件加速大规模科学计算 | 从MATLAB到C/C++代码

1. 用 CPU 做矩阵基本运算

假如我有两个10000x10000的矩阵（没错，1亿个元素），A和B，要对它俩进行相乘，得到C，用MATLAB表述是这样的：

A = rand(10000, 10000); % 随机产生10000x10000的矩阵
B = rand(10000, 10000); 
C = A*B;

如果简单直白地用 C 来实现矩阵乘法，它大概是这样子的：

  static double a[100000000];
  static double b[100000000];
  static double c[100000000];
  	double d;
  int i;
  int k;
  int xpageoffset;
  for (i = 0; i < 10000; i++) {
    for (xpageoffset = 0; xpageoffset < 10000; xpageoffset++) {
      d = 0.0;
      for (k = 0; k < 10000; k++) {
        d += a[i + 10000 * k] * b[k + 10000 * xpageoffset];
      }

      c[i + 10000 * xpageoffset] = d;
    }
  }

事实上，上述代码正是我从 MATLAB 自动生成的 C 代码里删节出来的。

将一个 MATLAB 里编写的函数或脚本文件生成 C 代码很简单，你可以通过 APP 菜单里的 MATLAB Coder 按提示一步一步来做，也可以通过命令行来实现，譬如下面几行指令可以将一个名为 largeMatrixTest.m 的脚本文件转换成 C 代码，并编译为 exe（借助 MinGW 或 Visual C++）：

cfg = coder.config('exe');
cfg.GenerateExampleMain = 'GenerateCodeAndCompile';
codegen largeMatrixTest -config cfg -report

如果你在同一台计算机上（譬如我的 Lenovo T480s），分别执行第一部分的 MATLAB 脚本和编译执行第二部分的 C 代码，效率会差多少呢？我得到的分别是 20.5 秒和…… 超过 30 分钟吧，真的没耐心等它执行完。那么问题来了，为啥 MATLAB 会比 C 还快？

如果你关注一下两者运行时 CPU 的占用率，你会发现，前者占用了你 CPU 的大多数核，CPU 总占用率达到了 70% 以上，而后者在我 4 核 8 线程的机器上只占用了 12% 的 CPU。MATLAB 是怎么做到的？答案是 BLAS（Basic Linear Algebra Subprograms），它是一个为底层向量与矩阵运算针对具体处理器高度优化实现的库，通过 BLAS，大规模矩阵运算便能利用计算机的多核来加速。BLAS 有 C 接口，我们当然可以手写 C 代码实现同样的加速，但显然没 MATLAB 那么容易.

有没有可能让 MATLAB 生成的 C 代码也能用到 BLAS 呢？答案是肯定的，参考这里就好: MATLAB 帮助文档

参照上面的文档，从 MATLAB 生成的 C 代码文件中我们可以看到，矩阵乘法运算 C=A*B 对应的代码是这样的：

  static double a[100000000];
  static double b[100000000];
  static double c[100000000];
  cblas_dgemm(CblasColMajor, CblasNoTrans, CblasNoTrans, (MKL_INT)10000,
              (MKL_INT)10000, (MKL_INT)10000, 1.0, &a[0], (MKL_INT)10000, &b[0],
              (MKL_INT)10000, 0.0, &c[0], (MKL_INT)10000);

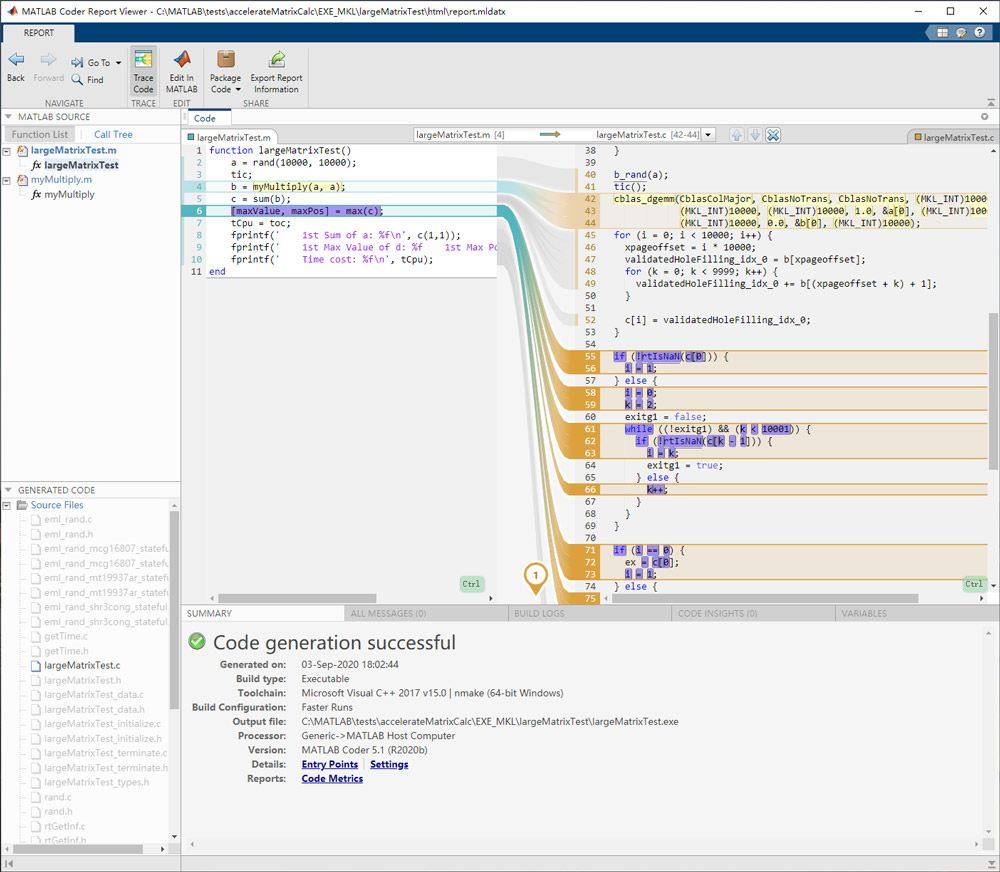
通过代码生成的报告我们还可以了解 m 脚本和生成的 C 代码之间的对应关系（如本文开头的图片所示）。

经过 BLAS 加持的 C 代码，跑起来效率就跟 MATLAB 脚本一样快了。

2. 用 CPU 做矩阵求解

BLAS 就够用了吗？不够。BLAS 实现了一些底层的计算，但如果要对矩阵进行求解（如奇异值分解或求特征值），我们还得借助 LAPACK 来加速。

MATLAB 中的 LAPACK

LAPACK（线性代数包）是一个例程库，它为数值线性代数和矩阵计算提供快速、稳健的算法。MATLAB 中的线性代数函数和矩阵运算均基于 LAPACK 构建，并且继续受益于其例程的性能和精度。

  • 简史

    MATLAB 诞生于 20 世纪 70 年代后期，是一款基于 LINPACK 和 EISPACK 构建的交互式计算器，而 LINPACK 和 EISPACK 在当时是进行矩阵计算的最先进的 Fortran 子例程库。多年来，MATLAB 使用了 LINPACK 和 EISPACK 的十几个 Fortran 子例程的 C 语言版本。

    2000 年，MATLAB 改用 LAPACK，这是 LINPACK 和 EISPACK 的现代替代品。它是一个用于数值线性代数的大型、多作者 Fortran 库。LAPACK 最初是为在超级计算机上使用而设计的，因为它能够一次计算矩阵的多个列。LAPACK 例程的速度与基本线性代数子例程 (BLAS) 的速度密切相关。BLAS 版本通常特定于硬件并经过高度优化。

  • 详见：

    参考 这个链接，可将 MATLAB 脚本中有关矩阵求解的函数（如 svd、eig 等）生成 LAPACK 调用。

3. 为 for 循环加速

看了前面两节的内容，我们已经知道，在 MATLAB 中，能直接对向量或矩阵做基本运算或调用某个函数去求解就不要自己写 for 循环来做了，因为 MATLAB 的向量 / 矩阵计算和求解基本都是 BLAS 和 LAPACK 加持过的。

但我们在实际计算中还是不可避免要有自己写的 for 循环，有些是顶层的循环，还有些可能是底层的没有可以直接拿来用的函数就自己写了。那么问题来了，自己 m 脚本里的 for 循环，无论是在 MATLAB 里还是生成 C 代码，跑起来都觉得慢怎么办？

我们知道，在 MATLAB 里把 for 换成 parfor，就可以通过并行计算工具箱利用单机多处理器或计算机集群硬件来加速，例如：

function a = test_parfor %#codegen
a=ones(10,256);
r=rand(10,256);
parfor (i=1:10, 4) % 指定4线程并发
  a(i,:)=real(fft(r(i,:)));
end
 
% codegen -config:lib test_parfor

那如果对上述脚本生成 C 代码，还能利用单机多核来加速吗？可以！

我们也可以从生成的代码中看到（截取部分如下所示），parfor 被实现成了多线程（用到了 OpenMP，详情可查阅 parfor 的帮助文档）。我们还可以通过 parfor 的参数来指定线程的数量，如 parfor (i=1:10, 4)，即指定为 4 线程。

#pragma omp parallel for \
 num_threads(4 > omp_get_max_threads() ? omp_get_max_threads() : 4) \
 private(b_i,yCol,b_r)

  for (i = 0; i < 10; i++) {
    /*  指定4线程并发 */
    for (b_i = 0; b_i < 256; b_i++) {
      b_r[b_i] = r[i + 10 * b_i];
    }

    c_FFTImplementationCallback_doH(b_r, 0, yCol);
    for (b_i = 0; b_i < 256; b_i++) {
      a[i + 10 * b_i] = yCol[b_i].re;
    }
  }

当然，如果你机器的CPU核数有限或者内存有限，尤其在BLAS和LAPACK或FFTW的并行化已经占用了大多数资源的情况下，期望再通过顶层的parfor提高整体运算效率可能就比较难了，此时你得先提高机器配置，让BLAS、LAPACK或FFTW能尽情施展后，再通过parfor激活for循环的并行化。又或者你的for循环里没有可通过BLAS、LAPACK或FFTW实现的并行化或者计算负载主要在非并行化的部分，可参考 这个链接 把 parfor 用起来。

4. 用 GPU 加速

大家可能听说过深度学习往往要用 GPU 来加速，这是因为深度学习的模型训练和实时推断都有超大的计算量。先撇开深度学习，在我们经典的科学计算中，怎么用 GPU 来加速呢？

首先，MATLAB 中利用 GPU 的方法很简单，我们来看下面的例子，C = A*B 然后对 C 矩阵做奇异值分解，你需要做的只不过是把矩阵 A 和 B 放进 GPU 内存罢了，MATLAB 会自动将后续的矩阵相乘和奇异值分解分配到 GPU 上完成。看代码：

function s = largeMatrixTest()
    coder.gpu.kernelfun;
    a = rand(5000, 5000);
    b = rand(5000, 5000);
    %c = a * b;
    gpuA = gpuArray(a);
    gpuB = gpuArray(b);
    c = gpuA * gpuB;
    s = svd(c);
end
% 执行下面的指令，可以统计运算所耗时间（与CPU上不同，用GPU做计算要用wait）：
dev=gpuDevice();tim=tic();largeMatrixTest;wait(dev);gpuTime=toc(tim);

尽管多出了两个内存搬运的操作，利用 NVIDIA GeForce GTX 1080 运行上面的脚本，结果比我 T480s 的 CPU 上跑相同的操作要 38 秒还是快了很多，只需要 11 秒了。那么大家应该知道，这归功于 CUDA。

上面的脚本能直接生成 CUDA 代码吗（C++）？然而并不能，因为 gpuArray 并不支持代码生成。那怎么才能生成调用 CUDA 库的 C++ 代码呢？答案是用最初的针对 CPU 的脚本，在生成时代码时指定用 GPU Coder 就行了。来看 m 代码：

%% largeMatrixTest.m
function s = largeMatrixTest()
    coder.gpu.kernelfun;
    a = rand(5000, 5000);
    b = rand(5000, 5000);
    c = a * b;
    %gpuA = gpuArray(a);
    %gpuB = gpuArray(b);
    %c = gpuA * gpuB;
    s = svd(c);
end

%% generate standalone exe by using GPU Coder (gpuCodeGenTest.m)
cfg = coder.gpuConfig('exe');
cfg.GenerateExampleMain = 'GenerateCodeAndCompile';
codegen largeMatrixTest -config cfg -report

是不是太简单了，只是将 CPU 代码生成时的 coder.Config 换成了 coder.gpuConfig，没错，就这么简单！但生成的代码就复杂多了，限于篇幅，这里就只截取 C=A*B 对应的函数和 svd 奇异值分解对应的函数，分别如下：

cublasDgemm(getCublasGlobalHandle(), CUBLAS_OP_N, CUBLAS_OP_N, 5000, 5000,
              5000, (double *)gpu_alpha1, (double *)&(*gpu_a)[0], 5000, (double *)
              &(*gpu_b)[0], 5000, (double *)gpu_beta1, (double *)&(*gpu_c)[0],
              5000);

cusolverDnDgesvd(getCuSolverGlobalHandle(), 'N', 'N', 5000, 5000, (double *)
                     &(*gpu_c)[0], 5000, &(*gpu_s)[0], NULL, 1, NULL, 1, (double
      *)getCuSolverWorkspaceBuff(), *getCuSolverWorkspaceReq(), &(*gpu_superb)[0],
                     gpu_info_t);

显然，这里分别用到了 CUDA 的 cuBLAS 和 cuSOLVER，另外，CUDA 也有 cuFFT。

如果你看的仔细，你可能还注意到了在 largeMatrixTest.m 这个脚本中，有一行特别的代码，coder.gpu.kernelfun，这是一行不影响执行但会影响代码生成的脚本，它告诉 GPU Coder，在为这个函数生成 C++ 代码时，将计算任务尽可能映射到 GPU 上去，MATLAB 会对脚本中的 for 循环进行分析，在允许的情况下为其生成为可并行化执行的函数。除此之位，我们还可以显式地通过 coder.gpu.kernel 将紧随其后的 for 循环加以并行化。

【备注】截至 R2020b，MATLAB 共提供 705 个可通过 gpuArray 利用 NVIDIA GPU 进行加速计算的函数；有 326 个函数可以生成利用 GPU 加速的 C++ 代码（即 CUDA 代码）。除此之外，MATLAB 内嵌并行化支持的函数也有 62 个，覆盖了深度学习训练、图像的非重复块处理、非线性优化、统计与机器学习、特征提取与工业统计等方方面面。众所周知，在计算性能方面，近 20 年来 MATLAB 的几乎每个版本更新都有所增强，如果你关心计算性能，用最新的版本是最好的选择。

5. 能支持 ARM 么？

上面的例子，无论是 Intel MKL 还是 CUDA，默认都是 x86/x86_64 平台的，操作系统可能是 Windows，也可能是 Linux，我不确切它们在 mac OS 会怎样，也许你可以自己尝试一下。

如果你在用基于 ARM 的系统，可以肯定的一点是，MATLAB 目前并没有能运行在 ARM 上的版本，也许以后会有，但如果你想把 MATLAB 上开发的算法生成 C/C++ 代码，跑到 ARM 上可以么？答案是肯定的。那如果要利用 ARM 上的特定核来加速行不行呢？

如果你的 ARM 上有 GPU 并支持 CUDA，那么可以肯定，上述第 4 节的内容依然适用，事实上，MATLAB 现在可以非常好地支持针对 NVIDIA Jetson 和 Drive 两个系列的产品的代码生成（参见 GPU Coder 相关文档）。

那如果没有 GPU，仅用 ARM 处理器能生成并行化加速的 C 代码么？答案应该是 ARM+Linux 架构上的 OpenBLAS、CLAPACK 和 FFT，以及 OpenMP 基础库。此外，ARM 也提供了一个 Arm Performance Libraries (commercial variant) ，大家可以去尝试一下。

【注】作者没有对 ARM 上的 BLAS、LAPACK 和 FFT 做任何测试，理论上可行，实际使用中如遇到问题，建议询问 MathWorks 中国办公室获得技术支持。

6. 其它

除了以上提到的内容，如今最热且重度依赖硬件加速的深度学习应用并没在本文中讨论，事实上 MATLAB 从 R2017b 就已经开始支持针对深度学习推断生成 C/C++ 代码，并可利用硬件来加速深度学习的推断，包括 NVIDIA 的桌面与服务器 GPU 及嵌入式 GPU（通过 CUDA 实现）、ARM Mali GPU 与 ARM Neon 核（通过 Arm Compute Library 实现），或者利用 x86_64 处理器的 SIMD（SSE/AVX，通过 Intel MKL-DNN 实现）。在最新的 R2020b 版本中，Deep Learning HDL Toolbox 还可以将训练好的深度学习模型生成为硬件描述语言，从而把深度学习部署到 FPGA 上。详情可参考 MATLAB 帮助文档或者咨询 MathWorks 中国办公室。

附录：利用 BLAS 和 LAPACK 的完整示例脚本

要从 MATLAB 生成 C 代码时支持 BLAS 和 LAPACK，你需要参照前面有关链接安装 INTEL MKL（含 BLAS 和 LAPACK），并从 coder.BLASCallback 和 coder.LAPACKCallback 分别派生自己的类，用来指定编译所需的头文件、库文件，它们的路径，以及所需的宏定义，最后在代码生成时指定这两个类，样例脚本如下：

%% example function for code generation (largeMatrixTest.m)
function largeMatrixTest()
    a = rand(5000, 5000);
    tic; 
    b = a * a;
    c = sum(a);
    s = svd(a);
    e = eig(a);
    [maxValue, maxPos] = max(a);
    tCpu = toc;
    fprintf('    Time cost: %f\n', tCpu);
end

%% define class for BLASCallback (useMyBLAS.m)
classdef useMyBLAS < coder.BLASCallback
    methods (Static)
        function updateBuildInfo(buildInfo, ~)
            libPath = 'C:\Program Files (x86)\IntelSWTools\compilers_and_libraries\windows\mkl\lib\intel64';
            libPriority = '';
            libPreCompiled = true;
            libLinkOnly = true;
            libs = {'mkl_intel_ilp64.lib' 'mkl_intel_thread.lib' 'mkl_core.lib'};
            buildInfo.addLinkObjects(libs, libPath, libPriority, libPreCompiled, ...
                                  libLinkOnly);
            buildInfo.addLinkObjects('libiomp5md.lib',fullfile(matlabroot,'bin', ...
                             'win64'), libPriority, libPreCompiled, libLinkOnly);
            buildInfo.addIncludePaths('C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2020.1.216\windows\mkl\include');
            buildInfo.addDefines('-DMKL_ILP64');
        end
        function headerName = getHeaderFilename()
            headerName = 'mkl_cblas.h';
        end
        function intTypeName = getBLASIntTypeName()
            intTypeName = 'MKL_INT';
        end
        function doubleComplexTypeName = getBLASDoubleComplexTypeName()
            doubleComplexTypeName = 'my_double_complex_type';
        end
        function singleComplexTypeName = getBLASSingleComplexTypeName()
            singleComplexTypeName = 'my_single_complex_type';
        end
        function p = useEnumNameRatherThanTypedef()
            p = true;
        end
    end
end

%% define class for LAPACKCallback (useMyLAPACK.m)
classdef useMyLAPACK < coder.LAPACKCallback
    methods (Static)
        function hn = getHeaderFilename()
            hn = 'mkl_lapacke.h';
        end
        function updateBuildInfo(buildInfo, buildctx)
            buildInfo.addIncludePaths(fullfile(pwd,'include'));
            libName = 'mkl_lapack95_ilp64';
            libPath = 'C:\Program Files (x86)\IntelSWTools\compilers_and_libraries\windows\mkl\lib\intel64';
            [~,linkLibExt] = buildctx.getStdLibInfo();
            buildInfo.addLinkObjects([libName linkLibExt], libPath, ...
                '', true, true);
            buildInfo.addIncludePaths('C:\Program Files (x86)\IntelSWTools\compilers_and_libraries_2020.1.216\windows\mkl\include');
            buildInfo.addDefines('HAVE_LAPACK_CONFIG_H');
            buildInfo.addDefines('LAPACK_COMPLEX_STRUCTURE');
            buildInfo.addDefines('LAPACK_ILP64'); 
        end
    end
end

%% generate standalone exe for above MATLAB function (genCodeTest.m)
cfg = coder.config('exe');
cfg.CustomBLASCallback = 'useMyBLAS';
cfg.CustomLAPACKCallback = 'useMyLAPACK';
cfg.GenerateExampleMain = 'GenerateCodeAndCompile';
codegen largeMatrixTest -config cfg -report

VIA:

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值