注:本文为涂鸦中数学故事合集。
–
数学史上最著名的涂鸦
原创 Arianrhod 原理
1843 年 10 月 16 日,爱尔兰数学家 哈密顿(William Rowan Hamilton,1805~1865)在都柏林皇家运河边散步时,突然迎来了一个顿悟时刻!
~
 ~
~
都柏林皇家运河上的布鲁姆桥上的一块牌匾,纪念了哈密顿的灵光一闪。(图 / William Murphy / Flickr, CC BY)
~

~
Photo of a plaque with inscription ‘Here as he walked by on the 16th of October 1843 Sir William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplication i 2 = j 2 = k 2 = i j k = − 1 i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1 & cut it on a stone of this bridge.’
A plaque on Dublin’s Broome Bridge commemorate’s Hamilton’s flash of insight. Cone83 / Wikimedia, CC BY-SA
都柏林布鲁姆大桥 (Broome Bridge) 上的一块牌匾纪念汉密尔顿 (Hamilton) 的灵光一闪。
他非常兴奋,拿出小刀,当场就把他得到的启示刻在了布鲁姆桥上:
i 2 = j 2 = k 2 = i j k = − 1 \Large i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1
这是数学史上最著名的涂鸦,虽然它看起来 “平平无奇”,但它却改变了数学家表示信息的方式,并使得无数的技术应用得以变得更加简单。那么,这个著名的涂鸦是什么意思呢?
旋转的物体
哈密顿试图解决的数学问题是,如何在 三维空间 中表示不同 方向 之间的关系。我们对方向并不陌生,它在描述力或速度等物理量时至关重要,但哈密顿感兴趣的是有关 三维旋转 的问题。
数学家已经知道如何用坐标(如 x 、 y 、 z x、y、z x、y、z)来表示物体的位置,但想要知道当这些物体在旋转时坐标发生了什么变化,就需要运用复杂的球几何。哈密顿想要一种更简单的方法。
他的灵感源自于一种表示 二维旋转 的方法,这种方法涉及到 复数。复数是由一个 实部 和一个 虚部 构成的,虚部是虚数*i* 的倍数,即 “-1 的平方根”。
i 2 = − 1 \Large i^2=-1 i2=−1
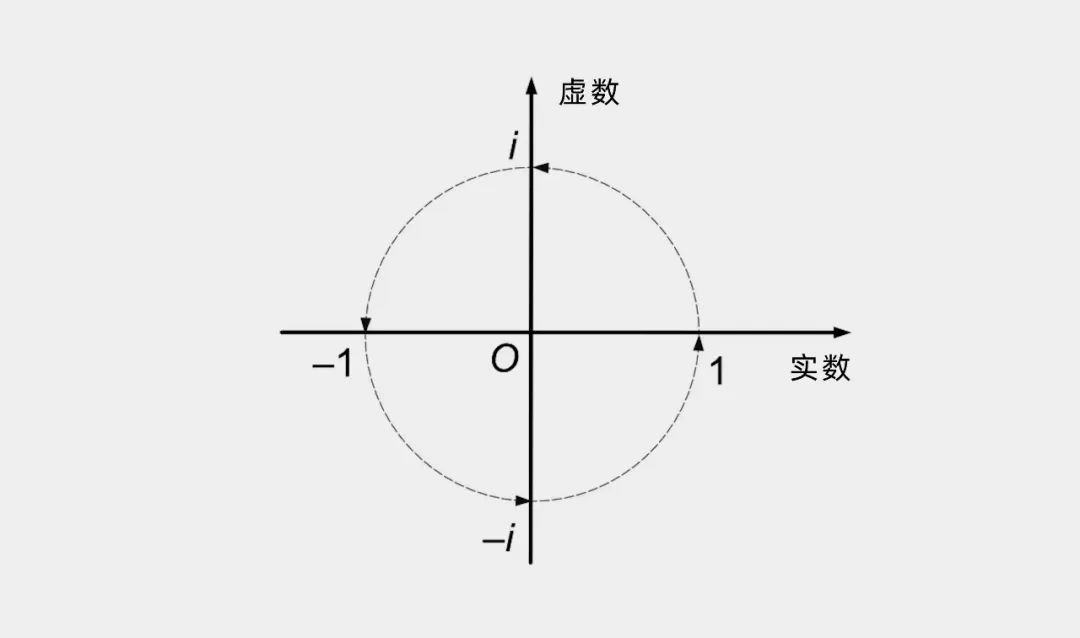
到 19 世纪初,包括 阿尔冈(Jean Argand)和 沃伦(John Warren)在内的几位数学家发现,复数可以用平面上的一个点来表示。沃伦还证明,要在这个复平面上将一条直线旋转 90°,在数学上是很容易办到的,因为这是当一个数乘以 i 的结果。
~
当把一个复数表示为复平面上的一个点时,将这个数字乘以 i i i,就相当于将相应的直线逆时针旋转 90°。
复数与几何之间的这种关联给了哈密顿启发,他开始尝试在三维空间中对其进行研究。他想象了一个三维复平面,沿着第二个虚数 j 的方向是第二个虚轴,这个虚轴垂直于另外两个轴。
他花了好几个月的时间才意识到,如果他想把二维旋转中的 “i 乘法” 扩展,那么 他需要具有第三个虚数 *k* 的四维复数。
在这个四维数学空间中, k k k 轴垂直于其他三个轴。而且 k 2 = − 1 k^2 = -1 k2=−1,并且根据定义, k = i j = − j i k = ij = -ji k=ij=−ji。结合这两个方程,就能得到
i j k = − 1 \Large ijk = -1 ijk=−1
把所有这些都结合在一起,就能得到关键的 i 2 = j 2 = k 2 = i j k = − 1 i^2 = j^2 = k^2 = ijk = -1 i2=j2=k2=ijk=−1 这个启示就像一道闪电,击中了布鲁姆桥上的哈密顿。
四元数和向量
哈密顿把他的四维数称为 “四元数”,并用它们来计算三维空间中的几何旋转。这也是今天人们用来移动机器人,以及定位卫星的旋转方式。但是大多数 “奇妙的用途” 只在仅考虑四元数的虚部时才会出现。这就是哈密顿所说的 “向量”。
四元数(Quaternions),是由爱尔兰数学家哈密顿(William Rowan Hamilton,1805-1865)在 1843 年发明的数学概念,直到 1985 年才由 Shoemake 把四元数引入到计算机图形学中。
一个向量可以同时编码两种信息,最著名的是如力、速度,或相对位置这类空间量的 大小和方向。
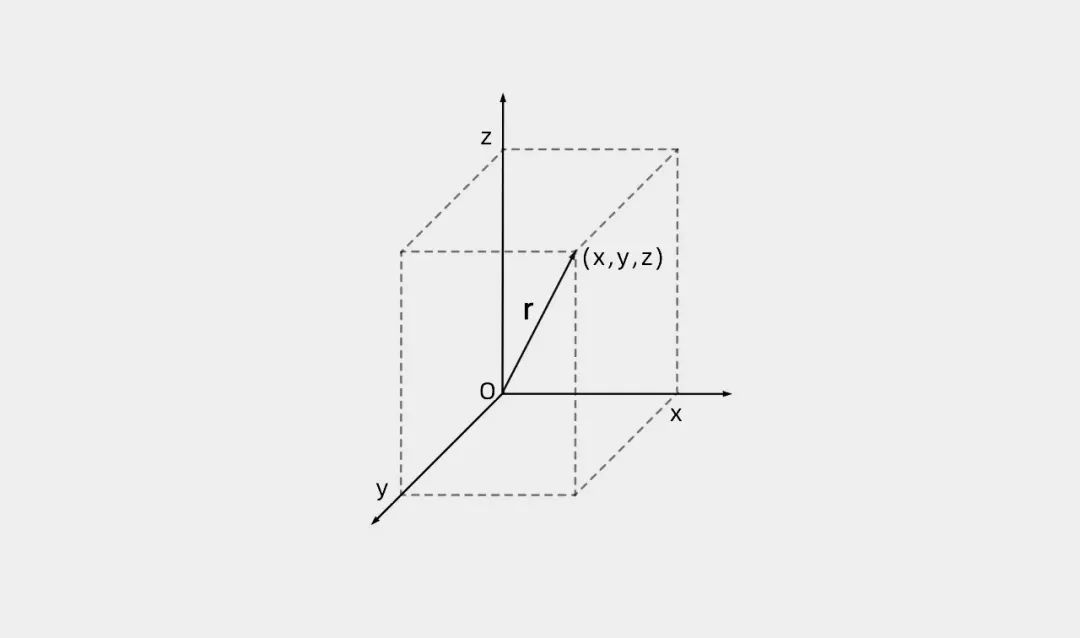
例如,为了表示一个物体相对于 “原点”(数轴上的零点)的位置 ( x , y , z ) (x, y, z) (x,y,z),哈密顿使用了一个从原点指向物体位置的箭头来表示。这个箭头表示位置向量: x i + y j + z k x \mathbf{i} + y \mathbf{j} + z \mathbf{k} xi+yj+zk。这个向量的 “分量” 是数字 x x x、 y y y、 z z z,也就是箭头沿着三个数轴中的每一个延伸的距离。
~
向量 r r r 就像从点 O 到坐标 ( x , y , z ) (x, y, z) (x,y,z) 的箭头。
半个世纪后,英国电报员亥维赛(Oliver Heaviside)帮助开创了现代向量分析,他用实单位向量 i 、 j 、 k i、 j、k i、j、k 取代了哈密顿的虚单位向量 i 、 j 、 k i、j、k i、j、k。但无论在哪种情况下,向量的分量都保持不变,因此箭头和向量乘法的运算法则也保持不变。
奥利弗・亥维赛(Oliver Heaviside,1850 年 5 月 18 日-1925 年 2 月 3 日),英国自学成才的物理学家。1880年,他研究电报传输上的集肤效应。他将在电磁学上举足轻重的麦克斯韦方程组重新表述,由四元数改为向量,将原来20条方程减到4条微分方程。
哈密顿定义了两种向量相乘的方法:一个产生的是数字,即所谓的 标量积 或 点积;另一个产生的是向量,即所谓的 向量积 或 叉积。如今,这些乘法在许多应用中都存在,例如支撑我们所有电子设备的电磁学方程。
一个数学对象
哈密顿不知道的是,其实在三年前,法国数学家 罗德里格(Olinde Rodrigues)就在关于旋转的研究中,提出了这些乘积的一个版本。把罗德里格的乘法称为向量的乘积是后见之明。而哈密顿是那个把这些分开的分量结合成一个单独的向量的人。
本杰明·奥林德·罗德里格斯(Benjamin Olinde Rodrigues,1795 年 10 月 6 日-1851 年 12 月 17 日)法国数学家,以其勒让德多项式公式而闻名。
其他人,从牛顿到罗德里格,都没能发展出一个单一的数学对象来统一地描述位置或力的分量。值得一提的是,还有一个人也有类似的想法,那就是自学成才的德国数学家 ——格拉斯曼(Hermann Grassmann),他独立地发展出了一个不那么直观的向量系统。
赫尔曼·京特·格拉斯曼(Hermann Günther Graßmann,1809年4月15日—1877年9月26日),出生于什切青,是一个德国博学者,在他生活的时代以语言学家身份闻名,今天以数学家身份而著称。他也是一位物理学家,新人道主义者,博学家和出版家。 什切青(Szczecin)现属波兰,在历史上,什切青的归属经历了多次变化。
哈密顿还发展了一套简洁的符号来使他的方程更简明优雅。他用希腊字母来表示四元数或向量,但在亥维赛之后,人们通常使用粗体的拉丁字母来表示。哈密顿的这种紧凑的符号改变了数学家在三维空间中表示物理量的方式。比如 麦克斯韦(James Clerk Maxwell)的电磁学方程就是很典型的例子。
∇ × E = − ∂ B ∂ t \displaystyle\nabla \times \mathbf{E} = -\frac{\partial \mathbf{B}}{\partial t} ∇×E=−∂t∂B
仅用少数几个符号,就展示了电场向量 (E) 在空间中的传播会如何受磁场向量 (B) 的影响。
如果没有向量符号,这样一个短短的公式将要被写成三个独立的方程(每个代表 B 和 E 的每个分量),每一个都是一堆坐标、乘法和减法。
∂ E z ∂ y − ∂ E y ∂ z = − ∂ B x ∂ t \displaystyle\frac{\partial E_{z}}{\partial y} - \frac{\partial E_{y}}{\partial z} = -\frac{\partial B_{x}}{\partial t} ∂y∂Ez−∂z∂Ey=−∂t∂Bx
− ∂ E z ∂ x + ∂ E x ∂ z = − ∂ B y ∂ t -\displaystyle\frac{\partial E_{z}}{\partial x} + \frac{\partial E_{x}}{\partial z} = -\frac{\partial B_{y}}{\partial t} −∂x∂Ez+∂z∂Ex=−∂t∂By
∂ E y ∂ x − ∂ E x ∂ z = − ∂ B z ∂ t \displaystyle\frac{\partial E_{y}}{\partial x} - \frac{\partial E_{x}}{\partial z} = -\frac{\partial B_{z}}{\partial t} ∂x∂Ey−∂z∂Ex=−∂t∂Bz
上述方程的展开形式。
毅力的力量
之所以选择麦克斯韦的一个方程作为例子,是因为麦克斯韦是第一个认识到这种简洁的向量符号拥有巨大潜力的主流物理学家。但可惜的是,哈密顿并没能活着看到麦克斯韦的支持。
不过,在面对主流的排斥时,哈密顿表现出了惊人的毅力。他希望终有一天,他的发现会被感激,这种愿望并非出自于虚荣心,而是他预见了一些可能的运用前景。
如果他知道向量在今天被如此广泛地使用,而且它们既可以表示数字信息,也可以表示物理信息,他应该会欣喜若狂。并且他会尤为高兴在旋转编程中,四元数仍然是最好的选择。
创作团队:
原文:Robyn Arianrhod(莫纳什大学)
排版:雯雯
参考来源:
-
Three letters, one number, a knife and a stone bridge: how a graffitied equation changed mathematical history
-
数学史上最著名的涂鸦 Arianrhod 原理 2024 年 10 月 18 日 21:45 浙江(三个字母,一个数字,一把刀和一座石桥)
篇外一:关于 i j k = − 1 i\, j\, k = -1 ijk=−1 的讨论
~
注:机翻,未校。
Quaternions: why does i j k = − 1 ijk = -1 ijk=−1 and i j = k ij=k ij=k and − j i = k -ji=k −ji=k
四元数:为什么 i j k = − 1 ijk = -1 ijk=−1 以及 i j = k ij=k ij=k 和 − j i = k -ji=k −ji=k
edited Apr 23, 2023 at 21:10
mau
asked Feb 6, 2013 at 15:54
Jordi Ozir
I do understand that i i i, j j j and k k k are imaginary numbers. so i 2 = j 2 = k 2 = − 1 i^2=j^2=k^2=-1 i2=j2=k2=−1. But I could not understand this:
我确实理解 i i i, j j j 和 k k k 是虚数。所以 i 2 = j 2 = k 2 = − 1 i^2=j^2=k^2=-1 i2=j2=k2=−1。但我不能理解这个:
i j = k ij=k ij=k, j k = i jk=i jk=i, k i = j ki=j ki=j, j i = − k ji=-k ji=−k, k j = − i kj=-i kj=−i, i k = − j ik=-j ik=−j
Why is this? There seems no explanation why that is true. I would like to understand why that is true instead of just assuming that that is true.
这是为什么?似乎没有解释为什么这是真的。我想理解为什么这是真的,而不仅仅是假设这是真的。
The defining properties relating i i i, j j j, and k k k are i 2 = − 1 i^2=-1 i2=−1, j 2 = − 1 j^2=-1 j2=−1, k 2 = − 1 k^2=-1 k2=−1, i j k = − 1 ijk=-1 ijk=−1.
定义 i i i, j j j, 和 k k k 的属性是 i 2 = − 1 i^2=-1 i2=−1, j 2 = − 1 j^2=-1 j2=−1, k 2 = − 1 k^2=-1 k2=−1, i j k = − 1 ijk=-1 ijk=−1.
From these you get for example that i ( i j k ) = i 2 j k = − i ⇒ j k = i i(ijk)=i^2jk=-i \Rightarrow jk=i i(ijk)=i2jk=−i⇒jk=i.
从这些你可以例如得到 i ( i j k ) = i 2 j k = − i ⇒ j k = i i(ijk)=i^2jk=-i \Rightarrow jk=i i(ijk)=i2jk=−i⇒jk=i.
These properties/definitions produce interesting and useful results, so we /axiomatically/ make them true for this structure. There is no deeper reason. We just want to study something that behaves in such a manner.
这些属性/定义产生了有趣和有用的结果,所以我们公理化地使它们对这种结构成立。没有更深层次的原因。我们只是想研究以这种方式表现的东西。
i, j, k are not imaginary numbers. Imaginary numbers arise only when you are talking about the complex plane C C C, which has a very simple one to one mapping with the 2-D plane R 2 R^2 R2. Quaternions arise when you are talking about three dimensions, i.e. looking for solutions to x 2 + 1 = 0 x^2+1=0 x2+1=0 in 3 − D 3-D 3−D .
i i i, j j j, k k k 不是虚数。虚数只有在你谈论复平面 C C C 时才会出现,它与 2 − D 2-D 2−D 平面 R 2 R^2 R2 有一个非常简单的一一映射。当你谈论三维时,会出现四元数,即在 3 − D 3-D 3−D 中寻找 x 2 + 1 = 0 x^2+1=0 x2+1=0 的解。
If you want to get a physical picture, consider i i i as rotating a vector or a line segment in 3 − D 3-D 3−D by 9 0 ∘ 90^\circ 90∘ taking X-axis as the axis of rotation. Similarly, j j j, k k k correspond to rotations about Y and Z axes respectively. This is similar to imaginary number i i i, which corresponds to a right angle rotation in the complex plane. Since in 3 − D 3-D 3−D there are more than one independent axes of rotation possible, 3 to be precise, there are 3 quaternions.
如果你想得到一个物理图像,考虑 i i i 作为在 3 − D 3-D 3−D 中旋转一个向量或线段 9 0 ∘ 90^\circ 90∘,以 X X X 轴为旋转轴。同样, j j j, k k k 分别对应于关于Y轴和Z轴的旋转。这与虚数 i i i 类似,它对应于复平面中的直角旋转。由于在 3 − D 3-D 3−D 中有多于一个独立的旋转轴可能,确切地说是 3 个,因此有 3 个四元数。
Now, two 9 0 ∘ 90^{\circ} 90∘ rotations about X, Y or Z axis will take the vector x \mathbf{x} x to its mirror image ( − x ) \mathbf{(-x)} (−x). So, i 2 = j 2 = k 2 = − 1 i^2=j^2=k^2 =-1 i2=j2=k2=−1.
现在,绕 X 、 Y X、Y X、Y 或 Z Z Z 轴旋转两次 9 0 ∘ 90^{\circ} 90∘,向量 x \mathbf{x} x 就会变成它的镜像 ( − x ) \mathbf{(-x)} (−x) 。所以, i 2 = j 2 = k 2 = − 1 i^2 = j^2 = k^2 = -1 i2=j2=k2=−1。
A right angle rotation about X axis followed by an equal amount of rotation about Y corresponds to an overall effective rotation of 9 0 ∘ 90^\circ 90∘ about Z axis. So, i j = k ij=k ij=k. Similarly, you can physically verify the quaternion multiplication laws.
关于X轴的直角旋转,然后是关于Y轴的等量旋转,对应于关于 Z Z Z 轴的总体有效旋转 9 0 ∘ 90^\circ 90∘。所以, i j = k ij=k ij=k。同样,你可以物理验证四元数乘法法则。
Do not try to think of their multiplication as arithmetic. They are compositions of rotation operations. If this looks too confusing, a little background in group theory will bring you enough mathematical maturity to be comfortable with these.
不要试图将它们的乘法视为算术。它们是旋转操作的组合。如果这看起来太令人困惑,那么一些群论的背景将给你带来足够的数学成熟度,以适应这些。
You can derive the properties of quaternions through clifford algebra and the geometric product of vectors.
你可以通过克利福德代数和向量的几何积来推导出四元数的属性。
The geometric product works like so:
几何积的工作方式如下:
e a e b = { 1 , a = b − e b e a , a ≠ b e_a e_b = \begin{cases} 1, & a = b \\ -e_b e_a, & a \neq b \end{cases} eaeb={1,−ebea,a=ba=b
where a , b a, b a,b can be x x x, y y y, or z z z as usual. This captures both the work of the cross product and the dot product in one product of basis vectors.
其中 a , b a, b a,b 可以是 x x x, y y y, 或 z z z 如常。这在一个基向量的乘积中同时捕捉了叉积和点积的工作。
You can then identify
然后你就可以识别
KaTeX parse error: {align*} can be used only in display mode.
And then the properties of quaternions naturally follow.
然后四元数的属性自然随之而来。
i 2 = ( − e y e z ) ( − e y e z ) = ( e y e z ) ( e y e z ) = − e y ( e z e z ) e y = − e y e y = − 1 i^2 = (-e_y e_z)(-e_y e_z) = (e_y e_z)(e_y e_z) = -e_y(e_z e_z)e_y = -e_y e_y = -1 i2=(−eyez)(−eyez)=(eyez)(eyez)=−ey(ezez)ey=−eyey=−1
And similarly for j 2 j^2 j2 and k 2 k^2 k2, as well as the i j k ijk ijk product:
以及 j 2 j^2 j2 和 k 2 k^2 k2,以及 i j k ijk ijk 乘积:
i j k = ( − e y e z ) ( − e z e x ) ( − e x e y ) = − e y e z e z e x e x e y = − e y ( e z e z ) ( e x e x ) e y = − e y e y = − 1 ijk = (-e_y e_z)(-e_z e_x)(-e_x e_y) = -e_y e_z e_z e_x e_x e_y = -e_y(e_z e_z)(e_x e_x)e_y = -e_y e_y = -1 ijk=(−eyez)(−ezex)(−exey)=−eyezezexexey=−ey(ezez)(exex)ey=−eyey=−1
This allows you to interpret quaternions in a very geometric way: the i i i, j j j, k k k do not represent vectors, but rather oriented planes. It’s just that in 3d each plane has a unique normal vector, so we often abuse this duality.
这允许你以非常几何的方式解释四元数: i i i, j j j, k k k 不代表向量,而是代表有向的平面。只是在 3 D 3D 3D 中每个平面都有一个唯一的法向量,所以我们经常滥用这种二元性。
But why are you identifying i i i as − e y e z -e_y e_z −eyez? By Clifford algebra, Subhadeep Ray Commented Jan 15 at 19:44
但是你为什么要把 i i i 识别为 − e y e z -e_y e_z −eyez 呢?在 Clifford algebra 代数中,
e y e z = e y ⋅ e z + i ∣ e y × e z ∣ = ∣ e y ∣ ∣ e z ∣ exp ( i π / 2 ) = i e_y e_z = e_y \cdot e_z + i |e_y \times e_z| = |e_y| |e_z| \exp(i \pi/2) = i eyez=ey⋅ez+i∣ey×ez∣=∣ey∣∣ez∣exp(iπ/2)=i.
It occurred to Hamilton during a walk to scratch into a bridge the following:
汉密尔顿在散步时想到在一座桥上刻下以下内容:
i 2 = j 2 = k 2 = i j k = − 1 i^2=j^2=k^2=ijk=-1 i2=j2=k2=ijk=−1
From this we deduce by basic algebra:
我们通过基本代数推导出:
i j = − i j k k = k ij = -ijkk = k ij=−ijkk=k
j k = − i i j k = i jk = -iijk = i jk=−iijk=i
k i = − 1 j k i = − 1 ki = -1jki = -1 ki=−1jki=−1
k i = − j j k i = j ki = -jjki = j ki=−jjki=j
i − 1 = − i − 1 i j k = − j k = − i i^{-1} = -i^{-1}ijk = -jk = -i i−1=−i−1ijk=−jk=−i
j − 1 = − j − 1 j k i = − k i = − j j^{-1} = -j^{-1}jki = -ki = -j j−1=−j−1jki=−ki=−j
k − 1 = − i j k k − 1 = − i j = − k k^{-1} = -ijkk^{-1} = -ij = -k k−1=−ijkk−1=−ij=−k
j i = j − 1 i − 1 = ( i j ) − 1 = k − 1 = − k ji = j^{-1}i^{-1} = (ij)^{-1} = k^{-1} = -k ji=j−1i−1=(ij)−1=k−1=−k
k j = − i kj = -i kj=−i similarly
i k = − j ik = -j ik=−j similarly
So we can provide complete arithmetic operations for the set numbers of the form a + i b + j c + k d a+ib+jc+kd a+ib+jc+kd:
所以我们可以为形式为 a + i b + j c + k d a+ib+jc+kd a+ib+jc+kd 的集合数提供完整的算术运算:
( a + i b + j c + k d ) ⋅ ( α + i β + j γ + k δ ) = a ( α + i β + j γ + k δ ) + i b ( α + i β + j γ + k δ ) + j c ( α + i β + j γ + k δ ) + k d ( α + i β + j γ + k δ ) = a α + i a β + j a γ + k a δ + i b α + i i b β + i j b γ + i k b δ + j c α + j i c β + j j c γ + j k c δ + k d α + k i d β + k j d γ + k k δ = ( a α − b β − c γ − d δ ) + i ( a β + b α + c δ − d γ ) + j ( a γ − b δ + c α + d β ) + k ( a δ + b γ − c β + d α ) \begin{array}{l} (a + i b + j c + k d) \cdot (\alpha + i \beta + j \gamma + k \delta) \\ = a (\alpha + i \beta + j \gamma + k \delta) + i b (\alpha + i \beta + j \gamma + k \delta) + j c (\alpha + i \beta + j \gamma + k \delta) + k d (\alpha + i \beta + j \gamma + k \delta) \\ = a \alpha + i a \beta + j a \gamma + k a \delta + i b \alpha + i i b \beta + i j b \gamma + i k b \delta + j c \alpha + j i c \beta + j j c \gamma + j k c \delta + k d \alpha + k i d \beta + k j d \gamma + k k \delta \\ = (a \alpha - b \beta - c \gamma - d \delta) + i (a \beta + b \alpha + c \delta - d \gamma) + j (a \gamma - b \delta + c \alpha + d \beta) + k (a \delta + b \gamma - c \beta + d \alpha) \end{array} (a+ib+jc+kd)⋅(α+iβ+jγ+kδ)=a(α+iβ+jγ+kδ)+ib(α+iβ+jγ+kδ)+jc(α+iβ+jγ+kδ)+kd(α+iβ+jγ+kδ)=aα+iaβ+jaγ+kaδ+ibα+iibβ+ijbγ+ikbδ+jcα+jicβ+jjcγ+jkcδ+kdα+kidβ+kjdγ+kkδ=(aα−bβ−cγ−dδ)+i(aβ+bα+cδ−dγ)+j(aγ−bδ+cα+dβ)+k(aδ+bγ−cβ+dα)
1 a + i b + j c + k d = a − i b − j c − k d ( a + i b + j c + k d ) ( a − i b − j c − k d ) = a − i b − j c − k d a 2 + b 2 + c 2 + d 2 \displaystyle \frac{1}{a + i b + j c + k d} = \frac{a - i b - j c - k d}{(a + i b + j c + k d)(a - i b - j c - k d)} = \frac{a - i b - j c - k d}{a^2 + b^2 + c^2 + d^2} a+ib+jc+kd1=(a+ib+jc+kd)(a−ib−jc−kd)a−ib−jc−kd=a2+b2+c2+d2a−ib−jc−kd
via:
-
Quaternions: why does i j k = − 1 ijk = -1 ijk=−1 and i j = k ij=k ij=k and − j i = k -ji=k −ji=k - Mathematics Stack Exchange edited Apr 23, 2023 at 21:10(关于 i j k = − 1 i\, j\, k = -1 ijk=−1 的讨论)
https://math.stackexchange.com/questions/296349/quaternions-why-does-ijk-1-and-ij-k-and-ji-k
篇外二: 关于布鲁姆大桥
Broome Bridge, Royal Canal, Broombridge Road, BALLYBOGGAN SOUTH, Dublin 7, DUBLIN
布鲁姆大桥, 皇家运河, 布鲁姆布里奇路, BALLYBOGGAN SOUTH, 都柏林 7, 都柏林
 ~
~
 ~
~
 ~
~

~
Survey Data 调查数据
~
| Reg No | 50060126 |
|---|---|
| Rating | National |
| Categories of Special Interest | Architectural, Historical, Social, Technical |
| Original Use | Bridge |
| Date | 1785 - 1850 |
| Coordinates | 313200, 237172 |
| Date Recorded | 16/08/2014 |
| Date Updated | –/–/– |
Description 描述
Two-arch limestone canal bridge of c.1790 and railway bridge of c.1845, carrying Broombridge Road on north-south axis over Royal Canal (north) and Dublin-Sligo railway line (south). Random coursed squared calp limestone walls with shallow piers flanking each arch having limestone ashlar plat-band to base of parapets and limestone ashlar coping. Elliptical arch to train bridge has rusticated limestone ashlar voussoirs and skewed squared calp soffit. Round arch to canal bridge has tooled limestone voussoirs and keystone with squared calp soffit. Canal bridge has Portland limestone plaque to northwest spandrel with inscription commemorating formula for quaternions devised by William Rowan Hamilton. Rubble stone embankment walls to either end have stacked coping. Break in east parapet provides access to steel footbridge to Broombridge Station. Tarmac carriageway follows steep gradient to both north and south approaches.
建于 1790 年的双拱石灰岩运河桥和建于 1845 年的铁路桥,南北轴线上承载着布鲁姆布里奇路,横跨皇家运河(北)和都柏林-斯莱戈铁路线(南)。随机的方形石灰石墙,每个拱门两侧都有浅桥墩,护墙底部有石灰石方石平台带和石灰石方石顶盖。通往火车桥的椭圆形拱门有质朴的石灰石方石拱腹和倾斜的方形 calp 拱腹。通往运河桥的圆拱有加工的石灰石拱门和带有方形 calp 拱腹的拱心石。运河桥的西北拱肩有波特兰石灰岩牌匾,上面刻有纪念威廉·罗文·汉密尔顿 (William Rowan Hamilton) 设计的四元数公式的铭文。两端的碎石路堤墙有堆叠的顶盖。东侧女儿墙的 Break 可通往 Broombridge 站的钢制人行天桥。柏油碎石车道沿着陡峭的坡度通往南北入口。
Appraisal 评价
Named after William Broome, a director of the Royal Canal Company. The canal section of the bridge is no doubt the older structure. It is of considerable significance for its associations with William Rowan Hamilton who. on the 16th October 1843, inscribed his mathematical formula for quaternions on to the bridge when out walking with his wife. The plaque under the bridge was unveiled by the Taoiseach Éamon de Valera, himself a mathematician and student of quaternions,on 13th November 1958. The railway bridge probably dates from the 1840s, while the two crossings now form a most appealing historic structure in the landscape at a junction of public transport and public amenity.
以皇家运河公司董事威廉·布鲁姆 (William Broome) 的名字命名。这座桥的运河部分无疑是较旧的结构。它与威廉·罗文·汉密尔顿 (William Rowan Hamilton) 的联系具有相当大的意义。1843 年 10 月 16 日,当他和妻子外出散步时,将他的四元数数学公式刻在了桥上。1958 年 11 月 13 日,桥下的牌匾由总理 Éamon de Valera 揭幕,他本人也是一位数学家和四元数的研究者。铁路桥的历史可能可以追溯到 1840 年代,而这两个道口现在在公共交通和公共设施的交界处形成了一个最具吸引力的历史建筑。
via:
-
Broome Bridge, Royal Canal, Broombridge Road, BALLYBOGGAN SOUTH, Dublin 7, DUBLIN - Buildings of Ireland(关于布鲁姆大桥)
当数学遇见艺术:谷歌涂鸦中的数学故事
原创 遇见数学
第一部分
谷歌常常用涂鸦(Doodle)方式改变首页上的 Logo 来庆祝各种重大事件、纪念著名历史人物、节日、成就和重要发现。这样的形式不仅娱乐性强,而且具有很高的教育价值,更能激发公众对某些主题的兴趣与了解。特别是在数学领域,谷歌就发布过不少涂鸦作品庆祝了许多重要的数学家与数学成就。
在本系列文章中,将按照谷歌发布时间的顺序,介绍与数学相关的涂鸦作品。
纪念法国数学家加斯顿·朱利亚

~
2004 年 2 月 2 日,Google 发布了一幅特别的涂鸦(可能是第一幅数学类作品),以纪念法国数学家加斯顿·朱利亚(Gaston Julia)诞辰 111 周年。

~
加斯顿·朱利亚(1893 年 2 月 3 日-1978 年 3 月 19 日)是一位著名的法国数学家,以其在复分析和动力系统理论方面的贡献而闻名。他最为人所知的成就是对迭代函数的研究,尤其是他对后来被命名为朱利亚集(Julia set)的分形结构的探索。
-
涂鸦中展示了迭代函数的数学公式 ,这是朱利亚集和曼德布罗特集合的数学基础公式。
-
涂鸦中还展示了三幅典型的分形图案,生动地展现了数学之美。
纪念天文学家珀西瓦尔·洛厄尔
2006 年 3 月 13 日,Google 以一幅涂鸦纪念美国天文学家珀西瓦尔·洛厄尔(Percival Lowell)诞辰 151 周年。

~
珀西瓦尔·洛厄尔(1855 年 3 月 13 日-1916 年 11 月 12 日),美国天文学家,以其对火星和其他行星的研究而闻名。他在亚利桑那州创立了洛厄尔天文台,这个天文台不仅是行星观测的重要基地,也是后来发现冥王星的地方。
-
洛厄尔最著名的理论是关于火星表面运河的存在。他认为这些运河是由智慧生命建造的,用来输送水资源。尽管后来证明这些运河是光学错觉,但他的研究激发了公众对火星和外星生命的兴趣。
-
洛厄尔在研究天王星和海王星的轨道时,预测了一个未知行星的存在,这个行星后来被称为“行星 X”。1930 年,克莱德·汤博在洛厄尔天文台发现了冥王星,这一发现验证了洛厄尔的预测。
这幅涂鸦以镶嵌其中的天文望远镜、地球和火星的元素来回顾洛厄尔在天文学领域的杰出贡献。其中火星上的两个外星人,这象征洛厄尔对火星运河的研究和对外星生命的猜想。
纪念建筑师米马尔·希南
2009 年 4 月 15 日,Google 发布一幅涂鸦,以纪念奥斯曼帝国最著名的建筑师之一米马尔·希南(Mimar Sinan)的诞辰 520 周年。涂鸦通过展示他设计的苏莱曼尼耶清真寺和塞利米耶清真寺等标志性建筑,颂扬了他在建筑艺术领域的卓越成就。

~
- 建筑和工程学科本身就与数学有着密切的联系。希南在他的设计中广泛应用了数学原理,确保建筑的稳定性和美观性。

~
塞利米耶清真寺主穹顶及其支撑结构的全视图, By Dosseman - Own work, CC BY-SA 4.0
-
几何学在他的建筑设计中起到了关键作用,尤其是在圆顶和拱形结构的设计中。
-
他对比例和对称性的应用,使得他的建筑作品不仅在视觉上令人惊叹,而且在结构上极为稳固。
纪念克里斯蒂安·惠更斯
2009 年 4 月 16 日,Google 以一幅涂鸦纪念了 17 世纪荷兰科学家克里斯蒂安·惠更斯(Christiaan Huygens)的诞辰。惠更斯是一名全才,他在光学、天文学、时间测量和概率论等多个科学领域都有着开创性的贡献。
~
这个涂鸦借由字母 g 展示了与他工作相关的元素,来纪念他的成就和对科学的贡献:
-
钟表和摆钟:象征了惠更斯在时间测量和钟表制造方面的革新。他发明的摆钟极大提高了时间测量的准确性,为后来的科学实验和海上导航提供了重要工具。
-
宇宙和天文元素:背景中的星空和天体象征了他在天文学方面的发现,包括土星环和土卫六。
-
光学元素:波纹状的图案可能象征了光的波动理论和惠更斯原理,展示了他在光学方面的贡献。
纪念祖冲之
2009 年 4 月 20 日,Google 发布了一幅特别的涂鸦来纪念中国古代数学家祖冲之。
~
祖冲之(429 年-500 年),字文远,是中国南北朝时期的著名数学家、天文学家和工程师。他在数学领域的贡献尤其突出,特别是他对圆周率(π)的精确计算。
-
祖冲之精确计算了圆周率(π)的值,他给出的 π 的近似值是 3.1415926 到 3.1415927 之间,这是当时世界上最精确的 π 值。
-
他还发现了两个非常精确的 π 的分数近似值: (约率)和 (密率)。特别是后者,在小数点第七位都是准确的,直到一千多年后才由 15 世纪的阿拉伯数学家阿尔·卡西以 17 位有效数字打破。
纪念数学家陈景润
2009 年 5 月 22 日,Google 发布了一个特别的 doodle 来纪念中国著名数学家陈景润的诞辰 76 周年。

~
陈景润(1933 年-1996 年)是我国杰出的数学家,以其在解析数论方面的重大贡献而闻名,特别是在哥德巴赫猜想研究中的突出成就。
哥德巴赫猜想是数论中的一个著名难题,提出所有大于 2 的偶数都可以表示为两个素数之和。
陈景润通过艰苦卓绝的研究,证明了“1+2”结果(即每个充分大的偶数可以表示为一个素数与至多两个素数乘积的和),这被称为“陈氏定理”,是对哥德巴赫猜想的一种重要进展。
涂鸦中的字母“l”由一大叠演算稿纸组成,上面放置的眼睛象征着陈老本人,反映了他在数学研究中的孜孜不倦和精益求精。
圆周率日
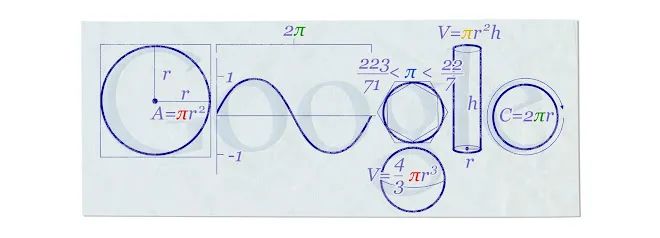
2014 年 3 月 14 日,Google 发布了一个特别的 doodle 来庆祝「Pi Day」,即圆周率日。这个 doodle 充满了与数学、尤其是与圆周率 π(Pi)相关的元素,展示了 π 在数学中的重要性和广泛应用。
~
这个涂鸦中包含了多个与 π 相关的元素与公式,具体如下:
- 圆面积公式:
- 在左边的图像中,有一个圆,标注了半径 ,并且写有圆的面积公式 。这是 π 在几何学中最基本和最常见的应用之一。
- 正弦函数图像:
- 右边紧挨着圆的是一个正弦函数的图像,周期为 。正弦函数是周期函数,其周期与 π 相关,广泛应用于三角学和信号处理。
- 圆周率的不等式:
- 中间部分展示了一个不等式 。这些是 π 的两个有名的有理数近似值,展示了 π 的精确值在两者之间。
- 六边形和内接圆:
- 右边有一个圆以及内接与外切六边形,展示了多边形与圆的逼近关系,这是古希腊数学家阿基米德用来近似计算 π 的方法。
- 球体和体积公式:
- 下方则展示了一个球体,写有其体积公式 ,这是 π 在计算球体体积中的应用。
- 圆柱体和体积公式:
- 右边还展示了一个圆柱体,标注了高度 和半径 ,并写有体积公式 。这展示了 π 在计算立体几何体积中的应用。
- 圆周公式:
- 最右边图像则展示了圆周公式,强调了 π 在确定圆形属性中的关键角色。
纪念地球物理学家米兰科维奇
2010 年 5 月 28 日,Google 发布了一幅涂鸦,纪念塞尔维亚天文学家和地球物理学家米卢廷·米兰科维奇(Milutin Milankovich)诞辰 131 周年。米兰科维奇因其对气候变化和冰河时代研究的贡献而知名,尤其是他提出的地球轨道参数变化对地球气候的影响,即著名的米兰科维奇循环理论。

~
涂鸦中,地球绕太阳的椭圆轨道象征了轨道离心率的变化,这是 Milankovitch 循环中的重要组成部分,它决定了地球接收到的太阳辐射量,从而影响全球气候模式。
第二部分
海萨尼·亚诺什·卡罗伊诞辰 90 周年
2010 年 5 月 29 日,Google 发布一副涂鸦来纪念海萨尼·亚诺什·卡罗伊(John Harsányi)诞辰 90 周年。

~
John Harsányi (1920-2000)是一位匈牙利裔美国经济学家,以其在博弈论方面的贡献而闻名。 他与 John Nash 和 Reinhard Selten 一起获得了 1994 年诺贝尔经济学奖,以表彰他们在非合作博弈理论中的均衡分析方面的开创性工作。

John Harsanyi
Harsányi 的工作与数学领域紧密相关。博弈论本身就建立在数学基础之上,Harsányi 的研究更是深入地使用了概率论、微积分等数学工具来分析和解决博弈问题。他最著名的贡献之一是**“不完全信息博弈”**理论,该理论拓展了博弈论的应用范围,使其能够更好地解释现实世界中的许多现象。
这副涂鸦中包含扑克牌、骰子和国际象棋,这三个元素象征着博弈论中的策略、概率和决策制定过程,共同构成了 Harsányi 研究的核心理念:在信息不对称、随机性和理性决策的情况下,如何找到博弈的均衡解。
卡希特·阿尔夫诞辰 100 周年
2010 年 10 月 11 日,谷歌发布了一幅涂鸦来纪念土耳其著名数学家卡希特·阿尔夫(Cahit Arf)的百年诞辰。
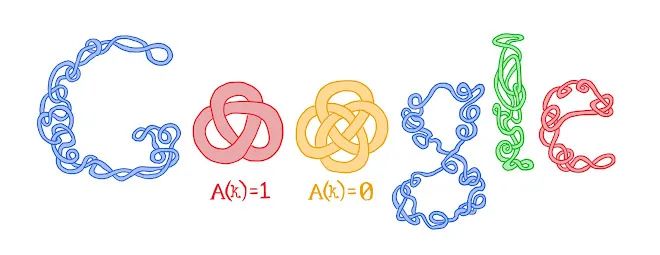
~
Arf 不变量是他的一个重要发现,它在二次型理论中起着关键作用,并且在代数拓扑中也有应用。这一发现帮助数学家研究和区分不同的代数结构和拓扑性质。

~
Cahit Arf
这幅涂鸦巧妙地将谷歌的字母设计成结的形状,并标注出结的 Arf 不变量,展示了数学的美丽和深度。
格雷戈尔·孟德尔诞辰 189 周年
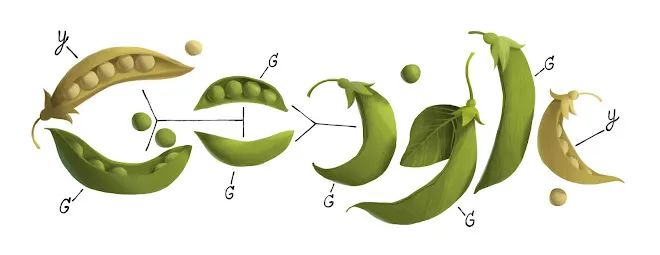
2011 年 7 月 20 日,谷歌发布了一幅涂鸦来纪念遗传学之父格雷戈尔·孟德尔(Gregor Mendel)诞辰 189 周年。
~
这幅涂鸦巧妙地结合了孟德尔最著名的豌豆杂交实验,展示了他对遗传学的开创性贡献:以豌豆荚和豌豆为主题,巧妙地将“Google”五个字母融入到豌豆荚和豌豆的形状中。每个字母都由不同的豌豆和豌豆荚组成,体现了孟德尔在豌豆实验中所观察到的遗传特征。涂鸦中还展示了豌豆的遗传符号(如“G”和“Y”),代表不同的遗传性状(绿色和黄色)。
谷歌将这幅涂鸦归类于数学,大概孟德尔在实验中所使用的数学工具,特别是统计方法,来分析他的交叉育种实验结果。其研究方法和结果显示了他在统计学和概率论方面的深刻理解。
皮埃尔·德·费马诞辰 410 周年
2011 年 8 月 17 日,谷歌发布一幅涂鸦来纪念法国著名数学家皮埃尔·德·费马(Pierre de Fermat)诞辰 410 周年。
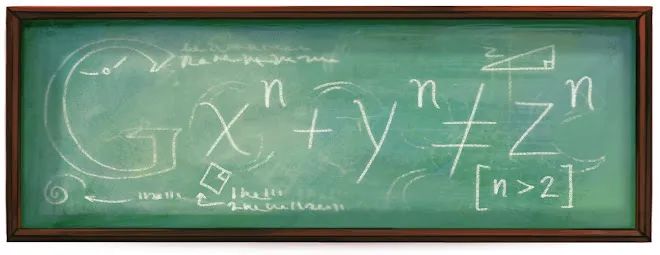
~
这幅涂鸦巧妙地融合了费马最著名的数学命题——费马大定理,作品以黑板为背景,上面用粉笔写下了费马大定理的表达式:。
另外,这似乎是数学类第一个互动的涂鸦——当鼠标移动到作品上时,会显出那句费马在书籍留白处所写下的那句话:
“I have discovered a truly marvelous proof of this theorem, which this doodle is too small to contain.”
我确信我发现一种美妙的证法,可惜这里的空白太小,写不下。
弗里乔夫·南森 150 周年诞辰
2011 年 10 月 10 日,谷歌发布涂鸦(Google Doodle)来纪念挪威极地探险家、科学家和人道主义者弗里乔夫·南森(Fridtjof Nansen)诞辰 150 周年。这幅涂鸦通过展现极地探险的场景,向南森的多方面贡献表示致敬。

~
作品中展示了被冰雪覆盖的地形和一艘探险船,南森身穿极地探险服,手持滑雪杖,形象生动。
谷歌将此涂鸦标记为数学主题,可能是因为南森的极地探险工作中涉及到了许多数学的应用——如导航、地理定位和制图等。
华罗庚 101 周年诞辰
2011 年 11 月 12 日,谷歌发布了一幅涂鸦来纪念我国著名数学家华罗庚(Hua Luogeng)诞辰 101 周年。这幅涂鸦通过生动的形象和数学符号,向华罗庚在数学领域的卓越贡献表示致敬。

~
这幅涂鸦展示了华罗庚的卡通形象,他戴着眼镜,穿着西装,在倒水的同时,似乎正在思考数学问题。

~
▲ 1964年华罗庚与数学竞赛优等奖学生进行交流(图自维基)
奥马尔·海亚姆 964 周年诞辰
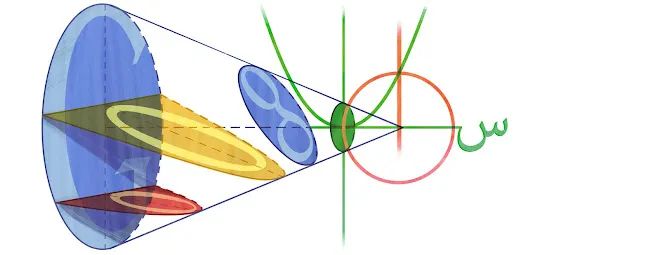
谷歌曾在 2012 年 5 月 18 日发布一副涂鸦纪念波斯著名诗人、数学家和天文学家奥马尔·海亚姆(Omar Khayyam)诞辰 964 周年。
~
这幅涂鸦的设计灵感来自于奥马尔·海亚姆在数学和天文学领域的成就。图中展示了几何图形,包括圆锥曲线(如抛物线、椭圆和双曲线)以及它们的截面,这些图形与海亚姆在代数和几何学中的研究密切相关。
艾伦·图灵百年诞辰
谷歌在 2012 年 6 月 23 日发布了纪念艾伦·图灵 100 周年诞辰的涂鸦。这款涂鸦以一种特别互动的方式向这位“计算机科学之父”和人工智能先驱致敬。

~
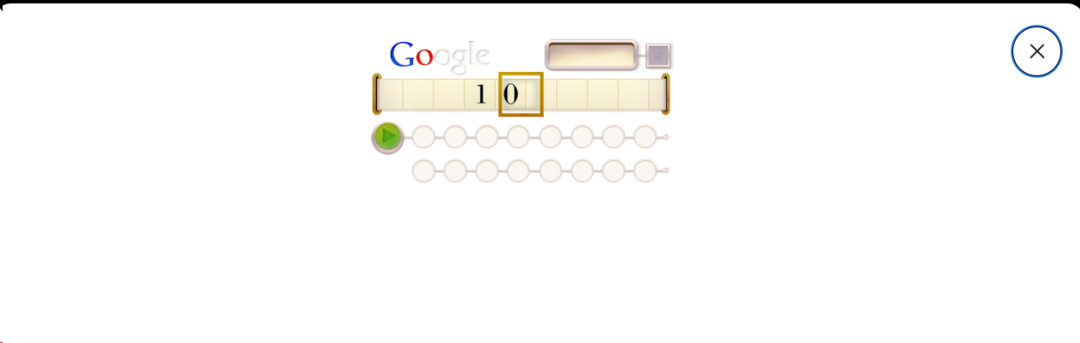
注意,这幅涂鸦能够互动,用户能够点击鼠标来模拟图灵机的行为。点击图片会进入互动界面,显示出图灵机的纸带,上面有一排排的 0 和 1,代表着二进制代码。
~
▲ 互动界面截图
可以通过点击涂鸦下方的按钮来操控纸带,模拟图灵机的读写操作。目标是按照提示,通过操控纸带上的 0 和 1 来拼写出“Google”的六个字母,以此体验图灵机的工作原理。
图灵机是计算理论的基石,它展示了什么可以被算法计算以及如何进行计算。艾伦·图灵通过他的工作,对计算机科学、人工智能以及密码学等领域产生了深远的影响。谷歌通过这幅动态涂鸦作品向这位伟大的科学家和他的贡献表示敬意。
阿布·比鲁尼的诞辰 1040 周年
2012 年 9 月 4 日,谷歌发布了一副涂鸦来纪念阿布·比鲁尼(Al-Biruni)诞辰 1040 周年。

~
这幅涂鸦描绘了阿布·比鲁尼观察夜空,反映了他在天文学上的兴趣和成就。
阿布·比鲁尼是一位著名的波斯学者,他的工作领域包括数学、天文学、地理学和历史学等。他被认为是中世纪伊斯兰世界最伟大的学者之一,对科学的发展做出了巨大的贡献。
玛雅历法长计数系统的结束
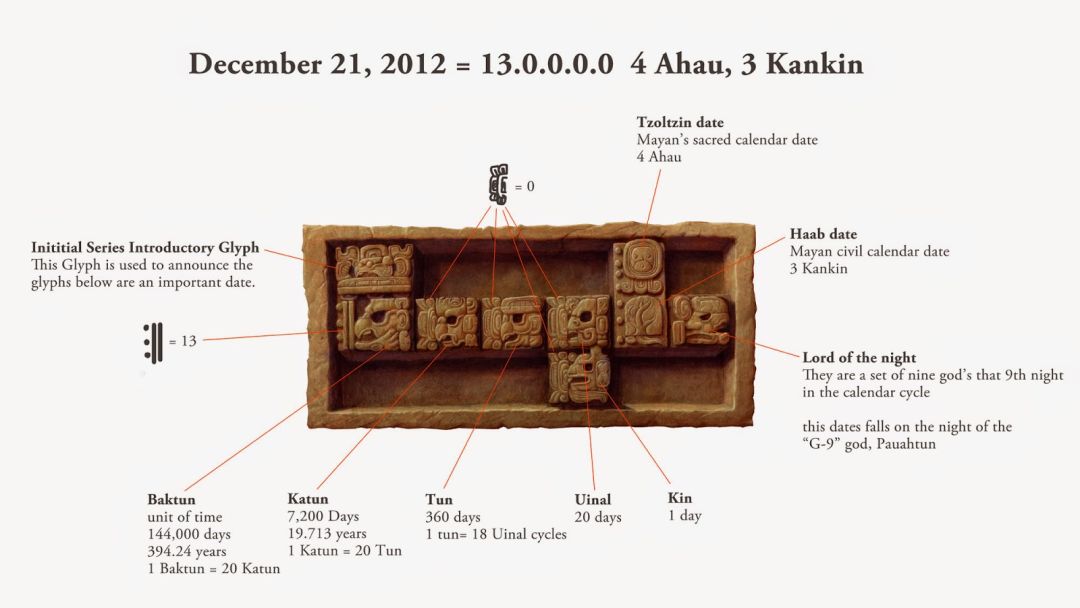
2012 年 12 月 21 日,谷歌发布了一副涂鸦来纪念“玛雅历法结束”(End of the Mayan Calendar)。这幅涂鸦庆祝了玛雅历法长计数系统(Mayan calendar Long Count System)第 13 个巴克图恩(Baktun)的结束。

~
巴克图恩是玛雅历法中的一个时间单位,每个巴克图恩大约相当于 394 年。第 13 个巴克图恩的结束引起了全球的关注和讨论,因为有人误解这意味着玛雅人预言了世界末日。然而,实际上,这仅仅标志着玛雅长计数历法的一个周期的结束和新周期的开始。
~
斯里尼瓦瑟·拉马努金诞辰 125 周年
这幅涂鸦发布于 2012 年 12 月 22 日,是为了纪念印度传奇数学家斯里尼瓦瑟·拉马努金(Srinivasa Ramanujan,1887 年 12 月 22 日-1920 年 4 月 26 日)诞辰 125 周年。

~
拉马努金是一位自学成才的天才数学家,在数论、无穷级数、连分数等领域做出了杰出贡献,对数学发展产生了深远影响。
家莱昂纳多·托雷斯·克维多诞辰 160 周年

~
这幅涂鸦发布于 2012 年 12 月 28 日,是为了纪念西班牙工程师兼数学家莱昂纳多·托雷斯·克维多(Leonardo Torres Quevedo,1852 年 12 月 28 日 - 1936 年 12 月 18 日)诞辰 160 周年。
克维多是一位杰出的发明家,在缆道运输、自动机、模拟计算等多个领域做出了开创性贡献。这幅涂鸦以克维多最著名的发明之一——西班牙阿兰胡埃斯皇家庄园的缆车为主题。
奈绥尔丁·图西诞辰 812 周年
2019 年 2 月 18 日,这幅谷歌发布涂鸦纪念奈绥尔丁·图西(Nasir al-Din al-Tusi)诞辰 812 周年。涂鸦展示了这位著名的波斯科学家和数学家,他在多个学科领域都有卓越的贡献。

~
奈绥尔丁·图西(Nasir al-Din al-Tusi,1201-1274)是波斯著名的学者,他在数学、天文学、哲学、医学、神学等领域都有深远的影响。他编写了大量的学术著作,其中一些作品在欧洲文艺复兴时期被翻译,并对欧洲的科学发展产生了重要影响。
图西在三角学方面的研究尤为突出,他是第一位将三角学作为独立学科进行研究的学者之一。
尼古拉·哥白尼诞辰 540 周年
2013 年 2 月 19 日,谷歌发布涂鸦以纪念尼古拉·哥白尼(Nicolaus Copernicus)诞辰 540 周年。涂鸦展示了哥白尼的日心说模型,这是他对现代天文学最重要的贡献。

~
尼古拉·哥白尼(Nicolaus Copernicus,1473-1543)是文艺复兴时期的波兰天文学家、数学家、和经济学家。他最著名的贡献是提出了日心说宇宙模型,这一理论在他的著作《天体运行论》(De revolutionibus orbium coelestium)中得到了详细阐述。
涂鸦以太阳为中心,这代表了哥白尼的日心说,即太阳是宇宙的中心,行星围绕太阳运行。这一理论颠覆了此前的地心说(地球是宇宙中心),对天文学的发展具有革命性意义。
莱昂哈德·欧拉诞辰 306 周年
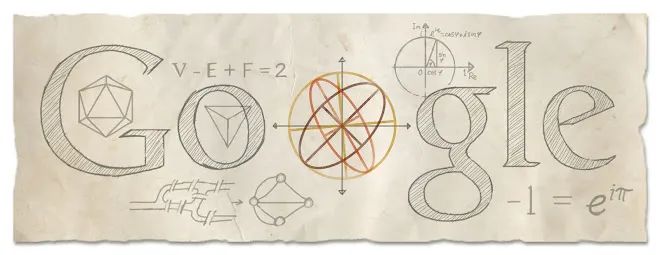
2013 年 4 月 15 日,谷歌发布涂鸦纪念莱昂哈德·欧拉(Leonhard Euler)诞辰 306 周年。涂鸦展示了欧拉在数学和物理学领域的多个主要贡献。
~
在涂鸦中,很多元素都与欧拉的著名贡献有关:
-
欧拉多面体公式: 涂鸦中间写有 ,这是欧拉多面体公式,描述了任意凸多面体的顶点数 、边数 和面数 之间的关系。
-
图论: 涂鸦左下方展示了一个图,象征着欧拉在图论方面的贡献。他在研究柯尼斯堡七桥问题时奠定了图论的基础。
-
欧拉公式:欧拉定义了复数的指数函数,并发现了它与三角函数的关系,这一关系式称为欧拉公式。
-
欧拉恒等式:当 就得到一个特例,称为欧拉恒等式:
-
欧拉角:用于描述三维空间中刚体的旋转,通过三个角度的组合,可以描述刚体的空间旋转过程。
此副涂鸦也能互动操作——欧拉角会随着鼠标方向动态旋转。
第三部分
纪念米哈伊洛·佩特罗维奇·阿拉斯诞辰 145 周年
这幅谷歌涂鸦发布于 2013 年 5 月 6 日,是为纪念塞尔维亚著名数学家、发明家和捕鱼达人(fisherman)米哈伊洛·彼得罗维奇·阿拉斯(Mihailo Petrović Alas)的 145 岁诞辰。

~
彼得罗维奇(1868 年 4 月 6 日-1943 年 6 月 8 日)是塞尔维亚著名的数学家和物理学家,以其在数学分析和微分方程领域的研究而闻名。他在贝尔格莱德大学教授数学,撰写了许多重要的数学论文和书籍。

~
▲ 塞尔维亚王储乔治和阿拉斯在一条大鱼旁合影(图自维基)
此外,他还热爱捕鱼,并经常在多瑙河和萨瓦河上垂钓,因此得到了“阿拉斯”(渔夫)的绰号。
纪念伊本·海什木诞辰 1048 周年
这幅谷歌涂鸦发布于 2013 年 7 月 1 日,是为纪念阿拉伯著名科学家、数学家和光学奠基人伊本·海什木(Alhazen)的 诞辰 1048 周年。涂鸦的设计灵感来源于伊本·海什木的光学研究和几何学成就。
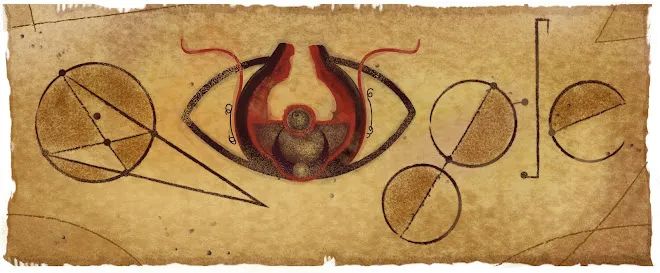
~
涂鸦中包含多个几何图形和光学元件,这些元素象征着伊本·海什木在光学和几何学方面的卓越贡献。特别是中央的眼睛形象,反映了他在视觉和光学方面的研究。

~
伊本·海什木(965 年-1040 年),全名阿布·阿里·穆罕默德·伊本·哈桑·伊本·海什木(Abu Ali al-Hasan ibn al-Haytham),是中世纪伊斯兰世界最著名的科学家之一,被誉为现代光学之父。他的研究涵盖了数学、天文学、光学、物理、医学和哲学等多个领域。
纪念夏琨塔拉·戴維诞辰 84 周年
这幅谷歌涂鸦发布于 2013 年 11 月 4 日,是为纪念印度著名数学家和心算天才夏琨塔拉·戴維(Shakuntala Devi)诞辰 84 周年。

~
Shakuntala Devi(1929 年 11 月 4 日-2013 年 4 月 21 日),被誉为“人类计算机”,以其超凡的心算能力而闻名于世。她在没有任何形式教育的情况下,展现了惊人的计算和记忆天赋,能够在极短的时间内完成复杂的数学计算。

~
夏琨塔拉·戴维,摄于1968年(图自维基)
涂鸦的设计灵感来源于 Shakuntala Devi 在心算和数学方面的非凡才能。涂鸦以电子计算器屏幕的形式呈现,巧妙地将“Google”的字样融入其中。
- 1977 年,戴维在美国与电脑同台竞技,看谁先算出 188,132,517 的立方根,结果她赢了。同年,在南美以美大学,她被要求计算一个 201 位数字的 23 次方根,并仅以 50 秒便得出了答案。(维基百科)
纪念格蕾丝·霍珀诞辰 107 周年
2013 年 12 月 9 日,谷歌发布一副涂鸦来纪念格蕾丝·霍珀(Grace Hopper)诞辰 107 周年。这幅涂鸦展示了她对计算机科学的巨大贡献。
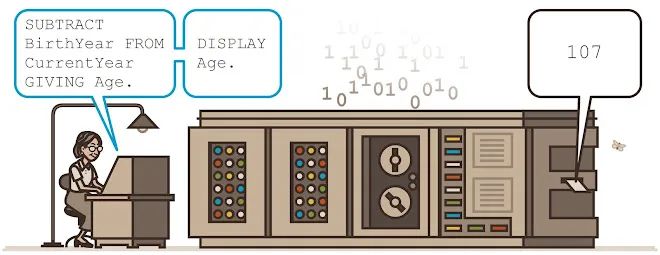
~
Grace Hopper(1906 年 12 月 9 日-1992 年 1 月 1 日),美国海军少将,是计算机科学领域的先驱之一。她在编程语言的开发和计算机科学的推广方面做出了巨大贡献。
-
霍珀发明了第一个编译器(A-0 系统)。
-
她是 COBOL(Common Business-Oriented Language)的主要设计者之一。
-
霍珀还创造了“调试”(debugging)一词。
涂鸦中显示了一个 COBOL 代码片段:“SUBTRACT BirthYear FROM CurrentYear GIVING Age”,这反映了她在编程语言上的贡献。背景中的大型计算机是霍珀工作的早期计算机(如 Mark I 计算机)。
纪念约翰内斯·开普勒诞辰 442 周年
谷歌在 2013 年 12 月 27 日发布了一副涂鸦来纪念约翰内斯·开普勒(Johannes Kepler)诞辰 442 周年。这幅涂鸦旨在向这位伟大的天文学家致敬。

~
约翰内斯·开普勒(Johannes Kepler,1571 年 12 月 27 日-1630 年 11 月 15 日),德国著名天文学家、数学家和占星家,是天文学革命的重要人物之一。他最为人知的是其行星运动三大定律,这些定律为天文学和物理学的发展奠定了基础。
纪念索菲娅·柯瓦列夫斯卡娅诞辰 164 周年
谷歌在 2014 年 1 月 15 日发布了一副涂鸦来纪念索菲娅·柯瓦列夫斯卡娅(Sofia Kovalevskaya)诞辰 164 周年。这幅涂鸦旨在向这位杰出的数学家和作家致敬。

~
Sofia Kovalevskaya(1850 年 1 月 15 日-1891 年 2 月 10 日)俄罗斯著名的数学家和作家。她是第一位在现代欧洲获得全职教授职位的女性数学家,也是首位获得数学博士学位的女性之一。
- 涂鸦中的第二个字母「O」代表了她在旋转刚体理论中的贡献。
纪念玛丽亚·加埃塔纳·阿涅西诞辰 296 周年
谷歌在 2014 年 5 月 16 日发布了一副涂鸦来纪念玛丽亚·加埃塔纳·阿涅西(Maria Gaetana Agnesi)诞辰 296 周年。这幅涂鸦旨在向这位杰出的意大利数学家、哲学家和语言学家致敬。

~
Maria Gaetana Agnesi(1718 年 5 月 16 日-1799 年 1 月 9 日),是 18 世纪意大利著名的数学家、哲学家和语言学家。她以其在微积分和分析领域的贡献而闻名,是数学史上重要的女性之一。
-
阿涅西最著名的著作是《分析学手册》,这是一本关于微积分和代数的教科书。这本书在当时被认为是最全面和最清晰的数学教科书之一。
-
她提出了一种著名的平面曲线(如涂鸦中所示),后来被称为阿涅西曲线。这条曲线在数学分析中有重要应用。
-
除了数学研究,阿涅西还积极参与教育和慈善事业,特别是帮助贫困和病患。
纪念埃米·诺特诞辰 133 周年
谷歌在 2015 年 3 月 23 日发布了一副涂鸦来纪念埃米·诺特(Emmy Noether)诞辰 133 周年。这幅涂鸦旨在向这位杰出的德国数学家致敬。

~
Emmy Noether(1882 年 3 月 23 日-1935 年 4 月 14 日),全名为 Amalie Emmy Noether,是 20 世纪最重要的数学家之一。她在抽象代数和理论物理领域做出了卓越贡献,特别是她的诺特定理在物理学中具有深远影响。
-
诺特定理是她最著名的贡献之一,该定理揭示了对称性与守恒定律之间的深刻联系。具体来说,它表明每一个连续对称性对应于一个守恒定律,对现代物理学的发展产生了巨大影响。
-
诺特在抽象代数领域的工作奠定了现代代数学的基础。她在环论、域论和线性代数等方面做出了开创性的贡献。
纪念阿布·瓦法诞辰 1075 周年
这副涂鸦发布在 2015 年 6 月 10 日,主题是纪念波斯数学家、天文学家、地理学家阿布·瓦法·布詹尼(Abu al-Wafa’ Buzjani)的诞辰 1075 周年。

~
阿波·瓦法·布兹贾尼(940 年 6 月 10 日-998 年 7 月 1 日)是中世纪伊斯兰世界著名的数学家和天文学家,生于布兹詹(今伊朗),后移居巴格达。他在数学特别是三角学和几何学方面有卓越的贡献。
纪念乔治·布尔诞辰 200 周年
谷歌在 2015 年 11 月 2 日发布了一副涂鸦来纪念 George Boole(乔治·布尔)诞辰 200 周年。这幅涂鸦旨在向这位杰出的数学家、逻辑学家和哲学家致敬。
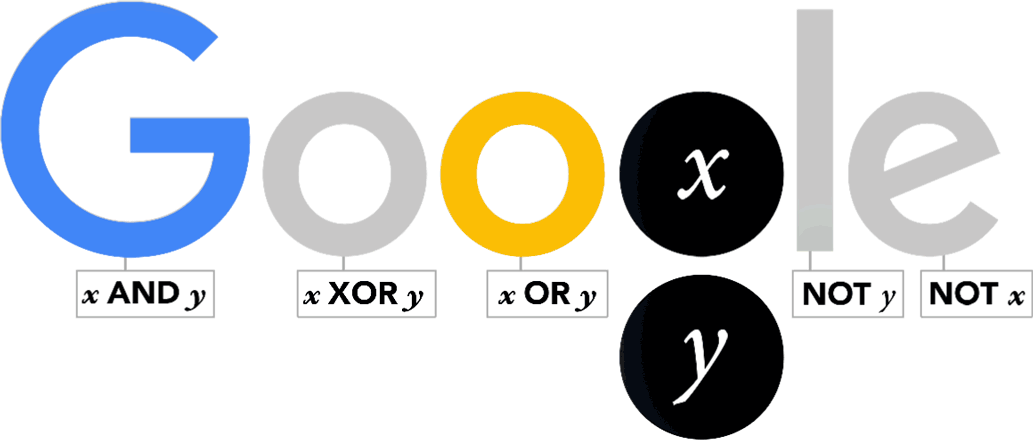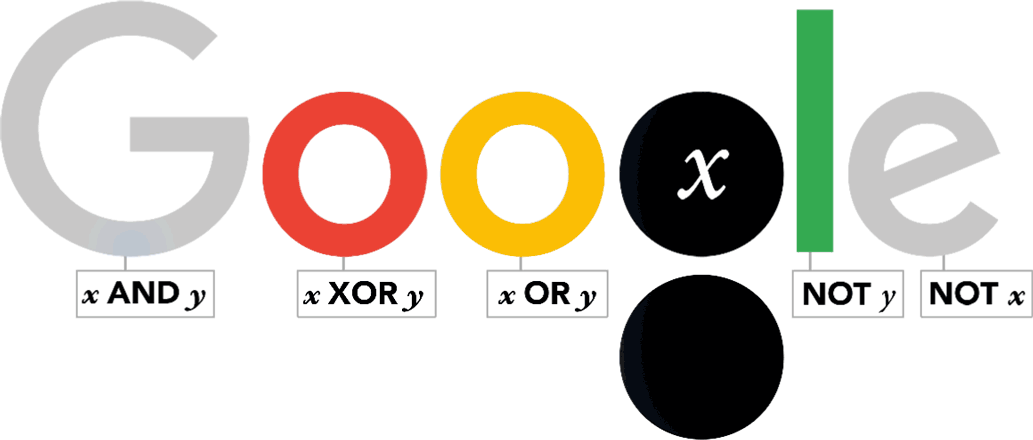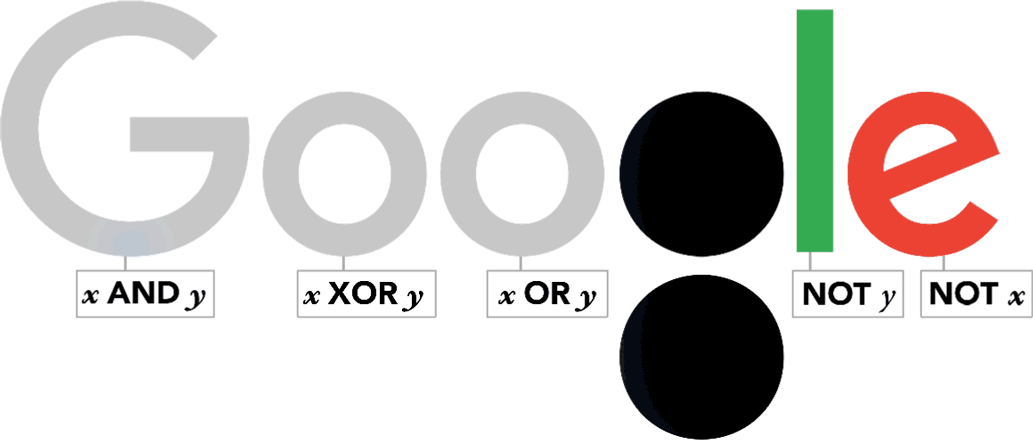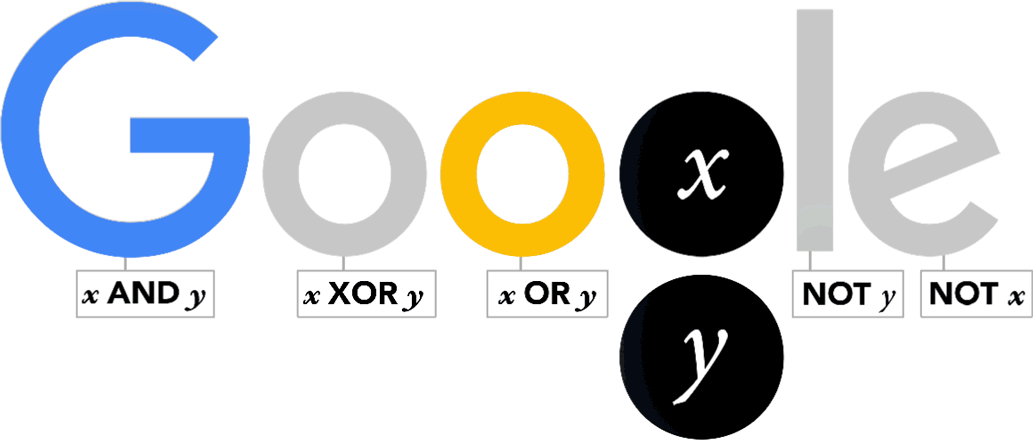
~
这幅涂鸦是动态的GIF格式
George Boole(1815 年 11 月 2 日-1864 年 12 月 8 日),是 19 世纪英国著名的数学家、逻辑学家和哲学家。他以其在数学逻辑和代数领域的贡献而著称,特别是他创立的布尔代数对现代计算机科学的发展具有深远影响。
-
布尔代数是布尔最重要的贡献之一,它是处理逻辑运算的代数系统。布尔代数中的操作(如 AND、OR、NOT)成为现代计算机科学和数字电路设计的基础。
-
布尔在其著作《逻辑和概率的数学分析探讨》中详细阐述了他的逻辑思想。这本书对逻辑学和概率论的发展起到了重要作用。
纪念乔治·佩雷克诞辰 80 周年
谷歌在 2016 年 3 月 7 日发布了一副涂鸦来纪念 Georges Perec(乔治·佩雷克)诞辰 80 周年。这幅涂鸦旨在向这位法国著名作家和电影人的非凡贡献致敬。

~
Georges Perec(1936 年 3 月 7 日-1982 年 3 月 3 日),是 20 世纪法国最具创新精神的作家之一。他是文学团体 Oulipo(潜在文学工场)的成员,以其实验性的写作风格和对语言的独特处理方式而闻名。
Oulipo,全称为“潜在文学工场”(Ouvroir de littérature potentielle),是 1960 年由数学家 François Le Lionnais 和作家 Raymond Queneau 创立的一个文学团体。该团体致力于通过数学和逻辑的方式探索文学创作的新方法。佩雷克作为 Oulipo 的活跃成员,他的许多作品都体现了这种数学和文学相结合的特质。
-
佩雷克的代表作之一《人生拼图版》(La Vie mode d’emploi)是一部结构复杂的小说,采用了拼图游戏的形式,被誉为 20 世纪最重要的文学作品之一,获得了 1978 年的梅迪西奖。
-
《消失》(La Disparition)是一部全篇没有使用字母“e”的小说,这种写作方法被称为“lipogram”。这部作品展示了佩雷克对语言和写作限制的探索。涂鸦中“Google”字样的最后一个字母“e”被擦去,就象征着佩雷克的这部作品。
纪念赫尔塔·马克斯·艾尔顿诞辰 162 周年
谷歌在 2022 年 4 月 28 日发布了一幅涂鸦,纪念 Hertha Marks Ayrton(赫尔塔·马克斯·艾尔顿)诞辰 162 周年。赫尔塔·马克斯·艾尔顿是英国杰出的工程师、数学家和发明家,她的研究成果对电弧灯和流体动力学的发展起到了重要作用。

~
Hertha Marks Ayrton(1854 年 4 月 28 日-1923 年 8 月 23 日),她是一位卓越的数学家和物理学家。她是第一位被英国皇家学会授予奖章的女性,并在科学界取得了显著的成就。
-
艾尔顿对电弧灯的研究极大地改善了其稳定性和效率。她发明了一个装置,能够自动调节电弧灯的电流,使其更加稳定和持久。
-
艾尔顿对流体动力学中的涡流和湍流现象进行了深入研究。她的论文《空气中的涡流》(The Origin and Growth of Ripple Marks)详细描述了这些现象的形成和发展机制。这幅涂鸦中就展示了涡流和流体动力学的示意图。
纪念克劳德·香农诞辰 100 周年
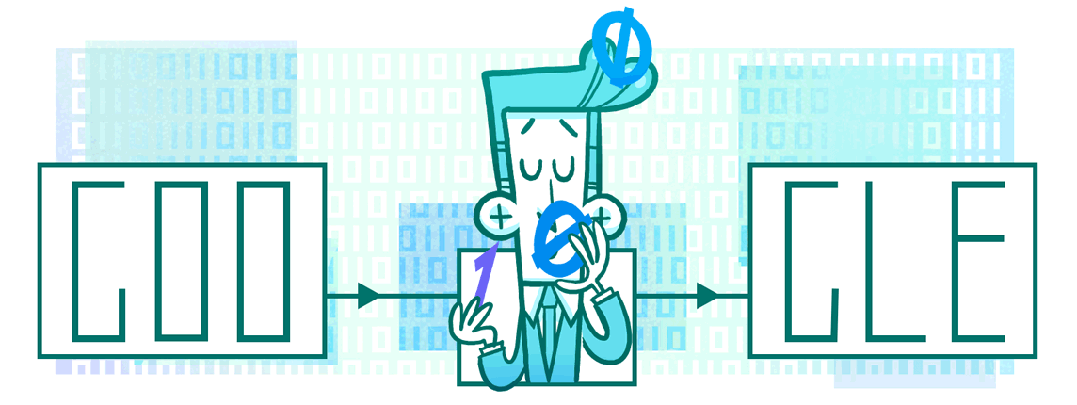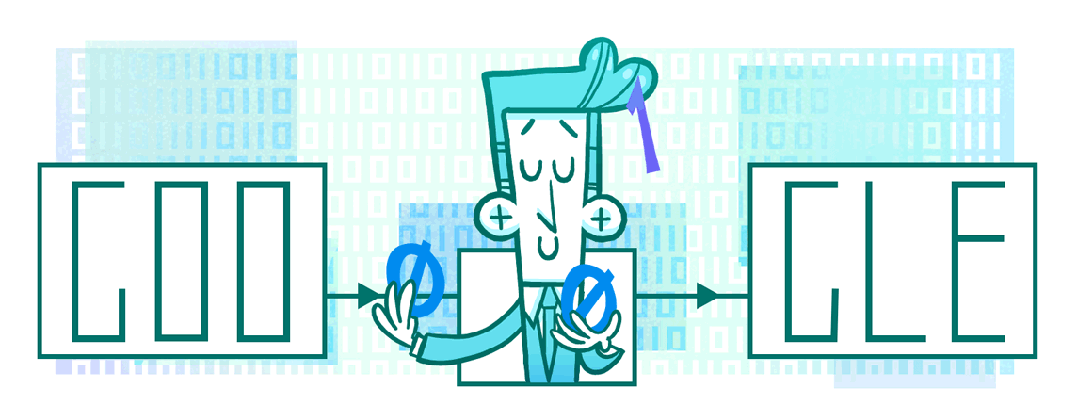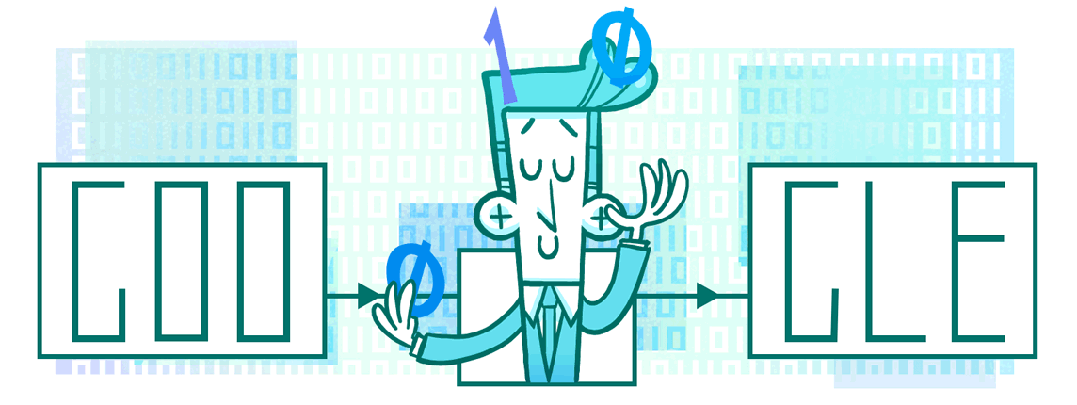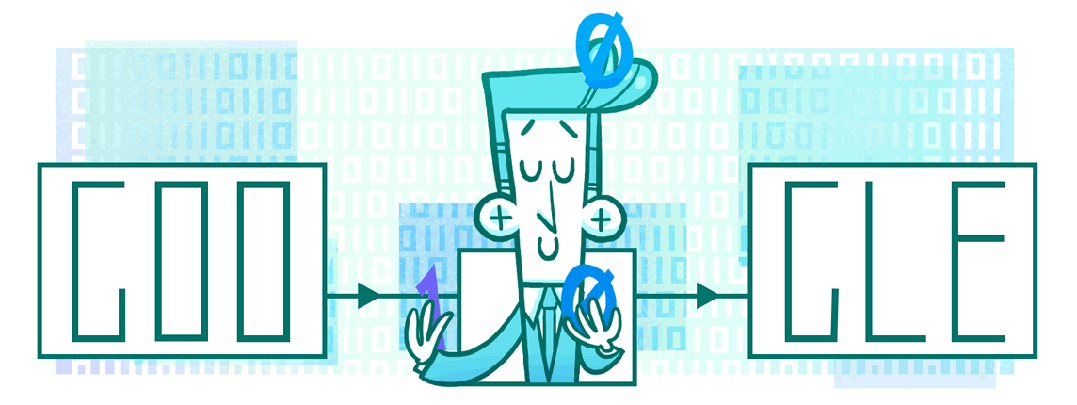
2016 年 4 月 30 日,谷歌发布了一幅涂鸦来纪念 Claude Shannon(克劳德·香农)诞辰 100 周年。克劳德·香农被誉为信息论之父,他的研究奠定了现代通信技术的基础,并在数学、电子工程和计算机科学领域产生了深远影响。
~
Claude Elwood Shannon(1916 年 4 月 30 日-2001 年 2 月 24 日),是美国著名的数学家、电气工程师和密码学家。他的开创性工作包括信息论、数字电路设计理论和密码分析等多个领域。
-
1948 年,香农发表了开创性的论文《通信的数学理论》(A Mathematical Theory of Communication),奠定了信息论的基础。他引入了“比特”(bit)的概念,作为信息量的基本单位,并提出了香农熵,用于量化信息的不确定性。
-
香农在硕士论文中首次将布尔代数应用于电路设计,提出了使用逻辑门实现复杂电路的方法。这一工作为现代数字计算机的设计提供了理论基础。
-
在第二次世界大战期间,香农也参与了密码学研究,他的工作对现代密码分析和信息安全产生了重大影响。
纪念弗里乔夫·南森诞辰 156 周年
谷歌在 2017 年 10 月 10 日发布了一幅涂鸦来纪念 Fridtjof Nansen(弗里乔夫·南森)诞辰 156 周年。

~
这幅涂鸦是第二幅关于南森的涂鸦作品,第一幅为纪念南森诞辰 150 周年所创作(请见之前的文章)。
纪念赤池弘次诞辰 90 周年
谷歌在 2017 年 11 月 5 日发布了一幅涂鸦,纪念赤池弘次(Hirotugu Akaike)诞辰 90 周年。赤池弘次是日本著名的统计学家,因提出了赤池信息量准则(Akaike Information Criterion, AIC)而广为人知。AIC 是统计模型选择的重要工具,在数据分析和统计建模领域具有广泛应用。

~
赤池弘次(1927 年 11 月 5 日-2009 年 8 月 4 日),出生于日本福冈县。他在统计学领域有着极高的声望,特别是在时间序列分析和信息理论方面。他的工作对现代统计学和数据科学的发展产生了深远的影响。

~
▲ 在创作初期的概念草图
第四部分
克里斯蒂安·多普勒诞辰 214 周年
2017 年 11 月 29 日,发布涂鸦纪念奥地利数学家、物理学家克里斯蒂安·多普勒(Christian Doppler)诞辰 214 周年。

~
克里斯蒂安·多普勒以发现和提出多普勒效应(Doppler Effect)而闻名。多普勒效应描述了波(如声波或光波)的频率或波长因观察者与波源相对运动而发生的变化。

~
多普勒效应在现实生活中有广泛应用,例如在气象雷达、天文学、医学超声波和测速设备中都能见到其应用。
庆祝圆周率日30周年
2018 年 3 月 14 日,发布涂鸦来纪念 Pi Day(圆周率日)的 30 周年。

~
圆周率日(Pi Day)是每年的 3 月 14 日,因为 3.14 是数学常数 π(圆周率)的前三位数字,因此这一天被选定为庆祝圆周率的日子。Pi Day 由物理学家赖瑞·萧(Larry Shaw)于 1988 年在美国旧金山的科学探索馆首次庆祝这个特殊日子。

~
By English Wikipedia user Ronhip, CC BY-SA 3.0
纪念高斯诞辰241周年
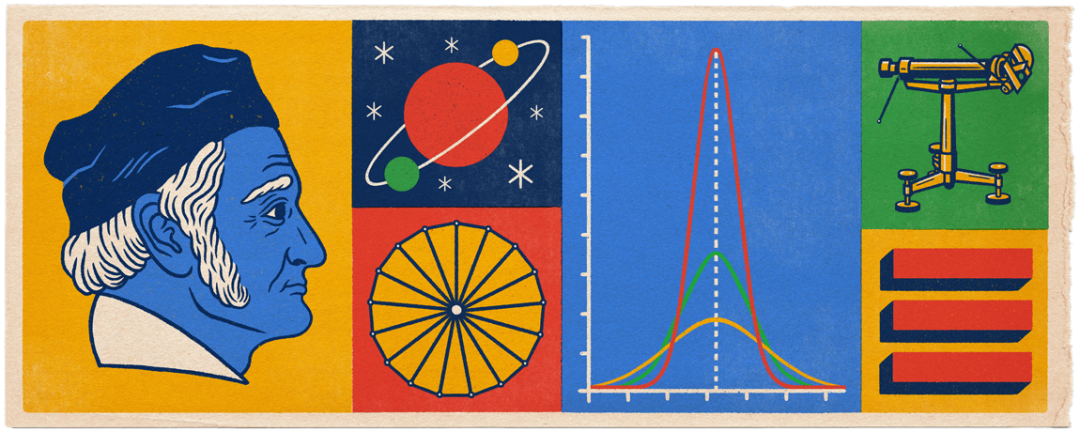
这幅涂鸦发布于 2018 年 4 月 30 日,是为纪念德国著名数学家、物理学家、天文学家和地理学家约翰·卡尔·弗里德里希·高斯(Johann Carl Friedrich Gauß)的诞辰 241 周年。
~
约翰·卡尔·弗里德里希·高斯(1777 年 4 月 30 日-1855 年 2 月 23 日),被誉为“数学王子”,是历史上最伟大的数学家之一。他在数论、代数、统计学、微积分、几何学、物理学和天文等多个领域做出了卓越的贡献。他的研究成果不仅在理论数学领域具有深远影响,还在实际应用中发挥了重要作用。
涂鸦中左侧为高斯的肖像,右侧巧妙地融入了他在各个领域代表成就。
萨洛瓦·拉乌达·舒凯尔诞辰102周年
这幅谷歌涂鸦发布于 2018 年 6 月 24 日,是为纪念黎巴嫩著名艺术家萨洛瓦·拉乌达·舒凯尔(Saloua Raouda Choucair)的诞辰 102 周年。
~
萨洛瓦·拉乌达·舒凯尔(1916 年 6 月 24 日-2017 年 1 月 26 日)是黎巴嫩现代艺术的先驱之一。她以其抽象的雕塑和绘画作品而闻名,其艺术风格受到伊斯兰艺术和西方现代主义的影响。她的作品强调形式、空间和几何的结合,展现了独特的艺术视角。
普拉桑塔·钱德拉·马哈拉诺比斯诞辰125周年
这幅谷歌涂鸦发布于 2018 年 6 月 29 日,是为纪念印度著名统计学家普拉桑塔·钱德拉·马哈拉诺比斯(Prasanta Chandra Mahalanobis)的诞辰 125 周年。

~
普拉桑塔·钱德拉·马哈拉诺比斯(1893 年 6 月 29 日-1972 年 6 月 28 日),是印度著名的统计学家,以其在统计学和经济规划方面的贡献而闻名。

~
马哈拉诺比斯
他是马哈拉诺比斯距离(Mahalanobis Distance)这一统计测量方法的发明者,在印度进行了人体测量学的开创性研究,也是印度统计研究所(Indian Statistical Institute)的创始人之一。他的工作对印度的经济和社会发展产生了深远影响。
纪念莱布尼茨诞辰372周年
这幅谷歌涂鸦发布于 2018 年 7 月 1 日,是为纪念德国著名数学家、哲学家和逻辑学家戈特弗里德·威廉·莱布尼茨(Gottfried Wilhelm Leibniz)的诞辰 372 周年。

~
戈特弗里德·威廉·莱布尼茨(1646 年 7 月 1 日-1716 年 11 月 14 日)是德国著名的数学家、哲学家、逻辑学家和科学家。他也是微积分的发明者之一,并在二进制系统、逻辑学和多种科学领域做出了重要贡献。莱布尼茨的工作不仅在数学和科学领域具有深远影响,他的哲学思想也对后来的哲学家产生了重大影响。
伊本·西那诞辰1038周年
这幅谷歌涂鸦发布于 2018 年 8 月 7 日,是为纪念波斯著名科学家、哲学家和医学家伊本·西那(Ibn Sina)的诞辰 1038 周年。

~
伊本·西那(980 年 8 月 22 日-1037 年 6 月),拉丁名阿维森纳(Avicenna),是中世纪伊斯兰世界最著名的科学家之一。

~
他的工作涵盖了医学、哲学、天文学、数学和化学等多个领域。伊本·西那最著名的著作是《医典》(The Canon of Medicine),这本书在很长一段时间内都是欧洲和伊斯兰世界的标准医学教科书。
奥尔加·拉德任斯卡娅诞辰97周年
这幅涂鸦发布于 2019 年 3 月 7 日,是为纪念俄罗斯数学家奥尔加·拉德任斯卡娅(Olga Ladyzhenskaya)诞辰 97 周年而创作。

~
奥尔加·拉德任斯卡娅(1922 年 3 月 7 日-2004 年 1 月 12 日)是 20 世纪著名的数学家,以其在偏微分方程和流体动力学方面的研究而闻名。

~
奥尔加(1976年)
她的工作对数学物理和应用数学的发展具有深远影响。拉德任斯卡娅在解决流体动力学中的纳维-斯托克斯方程和偏微分方程方面作出了杰出的贡献。
谷歌涂鸦页面评论:“今天的涂鸦纪念俄罗斯数学家奥莉加·拉德任斯卡娅,她克服了个人的悲剧和障碍,成为了她那个时代最有影响力的思想家之一”。
纪念奥马尔·海亚姆诞辰971周年
这幅谷歌涂鸦发布于 2019 年 5 月 18 日,是为纪念波斯著名诗人、数学家和天文学家奥马尔·海亚姆(Omar Khayyam)的诞辰 971 周年。

~
奥马尔·海亚姆(1048 年 5 月 18 日-1131 年 12 月 4 日)是中世纪波斯最著名的科学家和文学家之一。他因其在诗歌、数学和天文学方面的贡献而闻名于世。海亚姆在数学方面的成就主要包括系统研究三次方程并利用几何方法求解、对欧几里得几何学特别是平行公理的深入探讨,以及在数论方面对整数性质的研究,除此之外他的四行诗《鲁拜集》(Rubaiyat)在西方世界广为流传。
伊尔汉·科曼诞辰98周年
这幅谷歌涂鸦发布于 2018 年 6 月 17 日,是为纪念土耳其著名雕塑家伊尔汉·科曼(İlhan Koman)的诞辰 98 周年。

~
伊尔汉·科曼(1921 年 6 月 17 日-1986 年 12 月 30 日),是 20 世纪最杰出的土耳其雕塑家之一。他的作品以几何形态和动态结构而闻名,广泛应用于公共艺术和建筑装饰中。科曼的雕塑作品融合了科学、数学和艺术的元素,展示了他对形体和空间的独特理解。
纪念玛丽·萨默维尔诞辰240周年
这幅谷歌涂鸦发布于 2020年2月2日,是为纪念苏格兰著名科学家、数学家和科学传播者玛丽·萨默维尔(Mary Somerville)的诞辰240周年。

~
玛丽・萨默维尔(1780 年 12 月 26 日-1872 年 11 月 29 日),是一位杰出的苏格兰科学家和作家,她在数学、天文学、物理学和科学传播方面作出了重要贡献。她的著作不仅影响了当时的科学界,还在推动女性进入科学领域方面发挥了重要作用。

~
玛丽·萨默维尔,由Thomas Phillips 1834 所绘
萨默维尔最著名的工作之一是翻译并详细注释了皮埃尔-西蒙·拉普拉斯的《天体力学》(Mécanique Céleste),不仅阐明了拉普拉斯复杂的数学理论,还注释了前两卷的扩展版本,使这些理论更易于理解和接受。
纪念曼德博诞辰96周年
这幅谷歌涂鸦发布于 2020 年 11 月 20 日,是为纪念著名的数学家、分形几何之父本华·曼德博(Benoit Mandelbrot)的 96 周年诞辰。

~
本华·曼德博(1924 年 11 月 20 日-2010 年 10 月 14 日),是一位法国和美国的数学家,以创建分形几何学而闻名。他的工作在计算机图形学、物理学、金融市场和自然界中的复杂形态等多个领域产生了深远影响。曼德博最著名的成就是曼德博集合(Mandelbrot Set),它揭示了简单数学公式可以产生复杂而美丽的图形。
涂鸦中的分形图案在不断放大重复,象征着曼德博集合中无限的细节和复杂性,体现了分形几何学的核心思想。
纪念阿瑟·刘易斯爵士
这幅谷歌涂鸦发布于 2020 年 12 月 10 日,是为纪念诺贝尔经济学奖得主和发展经济学奠基人之一的阿瑟·刘易斯爵士(Sir W. Arthur Lewis)。

~
阿瑟·刘易斯(1915 年 1 月 23 日-1991 年 6 月 15 日)以其在发展经济学领域的开创性研究而闻名。1979 年,他与西奥多·舒尔茨(Theodore Schultz)共同获得诺贝尔经济学奖,以表彰他们在发展中国家经济增长方面的研究和贡献。刘易斯的“双部门模型”(或称刘易斯模型)特别著名,该模型解释了劳动力从传统农业部门向现代工业部门的转移过程。
埃米莉·杜·夏特莱诞辰315周年
这幅谷歌涂鸦发布于 2021 年 12 月 17 日,是为纪念法国著名数学家、物理学家和哲学家夏特莱侯爵夫人(Émilie du Châtelet)的诞辰 315 周年。

~
夏特莱(1706 年 12 月 17 日-1749 年 9 月 10 日)是 18 世纪法国杰出的数学家、物理学家和作家。她以翻译和注释艾萨克·牛顿的《自然哲学的数学原理》而闻名,这部译作至今仍然是法语世界中该书的标准译本。杜·夏特莱还在能量守恒定律和动力学方面做出了重要贡献,是启蒙时代少数几位女性科学家之一。
胡里奥·加拉维托诞辰157周年
这幅谷歌涂鸦发布于 2022年1月5日,是为纪念哥伦比亚著名天文学家和数学家胡里奥·加拉维托(Julio Garavito)的诞辰157周年。

~
胡里奥·加拉维托(1865 年 1 月 5 日-1920 年 3 月 11 日),是哥伦比亚杰出的天文学家和数学家。

~
他以对月球的研究而闻名,特别是他对月球轨道的研究和他对月球影响地球气候的理论。加拉维托还在多领域做出了重要贡献,包括数学、物理学和经济学。他的名字被用来命名月球上的一座环形山,以纪念他的科学成就。
纪念斯蒂芬·霍金诞辰80周年
这幅涂鸦发布于 2022 年 1 月 8 日,谷歌为纪念英国著名理论物理学家和宇宙学家斯蒂芬·霍金(Stephen Hawking)诞辰 80 周年而创作出来的。

~
斯蒂芬·霍金(1942 年 1 月 8 日-2018 年 3 月 14 日)是 20 世纪最著名的科学家之一,以其对黑洞和广义相对论的研究而闻名。他的著作《时间简史》使得复杂的科学概念更加易于大众理解。尽管在 21 岁时被诊断出患有肌萎缩性侧索硬化症(ALS),霍金依然以顽强的意志力和非凡的聪明才智在科学领域取得了卓越的成就。
原始页面中,点击这副涂鸦是可以观看一段视频。
纪念萨特延德拉·纳特·玻色
这幅谷歌涂鸦发布于 2022 年 6 月 4 日,是为纪念印度著名物理学家萨特延德拉·纳特·玻色(Satyendra Nath Bose)的科学成就。玻色因其在量子力学和统计力学方面的重要贡献而闻名,他的名字被用来命名玻色子。

~
萨特延德拉·纳特·玻色(1894 年 1 月 1 日-1974 年 2 月 4 日)是一位印度物理学家,他的工作为量子力学的发展奠定了基础。玻色最著名的贡献是与阿尔伯特·爱因斯坦合作提出的玻色-爱因斯坦统计及玻色-爱因斯坦凝聚,这一理论后来被用于解释光子、原子和其他粒子的行为。玻色子的概念也是基于他的研究,玻色子是遵循玻色-爱因斯坦统计的粒子。
玻色肖像旁边的图案是一个抽象的玻色子图形,代表了玻色在量子力学中的重要发现。
纪念斯特凡·巴拿赫
这幅涂鸦发布于 2022 年 7 月 22 日,是为纪念波兰著名数学家斯特凡·巴拿赫(Stefan Banach)的研究成就。

~
斯特凡·巴拿赫(1892 年 3 月 30 日-1945 年 8 月 31 日)是波兰著名的数学家,被认为是 20 世纪最伟大的数学家之一。他是现代函数分析的创始人之一,并对拓扑学、测度论和积分几何等领域做出了重大贡献。巴拿赫空间(Banach space)这一概念即是以他的名字命名的。
在上面系列文章中,我们一起回顾了谷歌发布的众多与数学相关的涂鸦作品,从埃舍尔到巴拿赫,再到其他众多数学界的巨擘。这些涂鸦不仅仅是对这些数学家的致敬,更是对数学这一科学的赞美。每幅作品背后都有一段动非凡的人生,每一个符号和公式都蕴含着无穷的智慧和创造力。
via:
-
当数学遇见艺术:谷歌涂鸦中的数学故事(第一部分)原创 遇见数学 2024年05月23日 20:19 河南
-
当数学遇见艺术:谷歌涂鸦中的数学故事(第二部分 原创 遇见数学 遇见数学 2024年05月30日 20:01 河南
-
当数学遇见艺术:谷歌涂鸦中的数学故事(第三部分)原创 遇见数学 2024年06月18日 20:01 河南
-
当数学遇见艺术:谷歌涂鸦中的数学故事(第四部分)原创 遇见数学 遇见数学 2024年07月16日 20:01 河南
























 4648
4648

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








