Vrms / Vm / Vpk

斐夷所非

已于 2025-02-09 10:08:51 修改

阅读量701

点赞数 6

分类专栏： electronic engineering 文章标签： Vrms

于 2025-02-09 00:40:33 首次发布

本文链接：https://blog.csdn.net/u013669912/article/details/145513642

版权

electronic engineering 专栏收录该内容

42 篇文章

订阅专栏

注：机翻，未校。

VRMS

What is a VRMS?

VRMS stands for root - mean - square voltage.
VRMS 代表均方根电压。

Why is RMS used?

Unlike DC voltages which are constant over time, AC (alternating current) voltages are time-varying and sinusoidal in shape. The RMS value of an AC signal is equivalent to the DC voltage that would be required to produce the same heating effect (power). The RMS of mains electricity in the U.S. is 110 V and in Europe it is 220 V.
与随时间恒定的直流电压不同，交流（AC）电压是随时间变化的，且形状为正弦波。交流信号的 RMS 值等于产生相同热效应（功率）所需的直流电压。美国市电的 RMS 为 110 伏，欧洲为 220 伏。

How is RMS voltage different to the average voltage?

RMS 电压与平均电压有何不同？

A sinusoidal signal (Figure 1) alternates between a peak positive and peak negative value once every cycle. Therefore, the average value of the signal is zero, so the average value of the signal is not a useful quantity. The power of an AC signal is used on both the positive and negative cycles. RMS is calculated using the square of signal voltage values at specific points in time. Since squaring eliminates negative numbers, it incorporates the contribution of the negative values. In this way, it is similar to calculating the standard deviation of a set of numbers which have a mean of zero.
正弦信号（图 1）在每个周期内，在正峰值和负峰值之间交替变化。因此，该信号的平均值为零，所以信号的平均值并非一个有用的量。交流信号的功率在正、负周期都起作用。RMS 是通过在特定时间点的信号电压值的平方来计算的。由于平方运算会消除负数，所以它包含了负值的贡献。从这个角度看，它类似于计算一组平均值为零的数字的标准差。

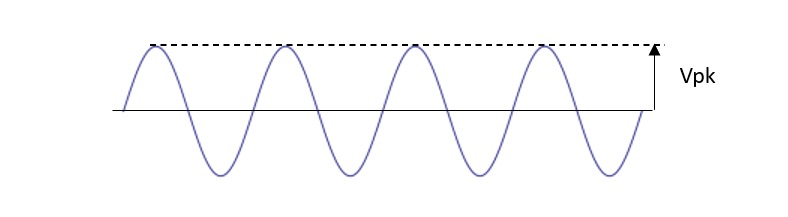
sinusoidally varying ac signal vrms

Figure 1. Sinusoidally varying AC signal
图 1.正弦变化的交流信号

What is the relationship between RMS and peak voltage?

RMS 和峰值电压之间有什么关系？

The formula that relates $V_{RMS}$ and $V_{pk}$ is:
将 $V_{RMS}$ 和 $V_{pk}$ 联系起来的公式为：

$V_{pk}=\sqrt{2}V_{RMS}$

What is the difference between $V_{rms}$ and $V_m$ ?

edited Jun 2, 2024 at 10:50 Greenonline
answered Apr 8, 2013 at 17:01 hassa hassan789

1. RMS（均方根值， $V_{rms}$ ）

If you had a DC voltage of 10 V and a 1 ohm resistor, the power dissipated in the resistor is 100 W because:

如果你有一个 10 V 的直流电压和一个 1 欧姆的电阻，电阻上消耗的功率为 100 W，因为：

$\frac{V^2}{R}$

The RMS value of 10 VDC is 10 VDC — it’s the number you use to calculate power in DC circuits.

10 V 直流电压的均方根值（RMS）为 10 VDC —— 这是用于计算直流电路中功率的数值。

In simple sinusoidal AC circuits, if you have a peak value of 10 V, you will find that it dissipates in a 1 ohm resistor somewhat less than 100 W.

在简单的正弦交流电路中，如果你有一个 10 V 的峰值电压，你会发现它在 1 欧姆的电阻上消耗的功率会小于 100 W。

It will dissipate 50 W — and if you reverse the process to work out what peak sine voltage would cause it to dissipate 100 W you’ll find it to be 14.14 V (approx).

它会消耗 50 W —— 而如果你反过来计算，要使它消耗 100 W，所需的正弦波峰值电压约为 14.14 V。

Most engineers are so well-versed in doing this that it may seem, to the uninitiated, that there is no theory behind it. I acquired this from the web: -

大多数工程师对这种计算非常熟悉，以至于对于初学者来说，似乎背后没有理论支持。我从网上找到了以下内容：

Root-Mean-Square Voltage (Vrms)

均方根电压（ $V_{rms}$ ）

As the name implies, $V_{rms}$ is calculated by taking the square root of the mean average of the square of the voltage in an appropriately chosen interval.

顾名思义， $V_{rms}$ 是通过对在适当选择的区间内电压平方的平均值取平方根来计算的。

In the case of symmetrical waveforms like the sinewave, a quarter - cycle faithfully represents all four quarter - cycles of the waveform.

对于像正弦波这样的对称波形，四分之一周期如实地代表了该波形的所有四个四分之一周期。

Therefore, it is acceptable to choose the first quarter - cycle, which goes from 0 radians ( $0^{\circ}$ ) through $\pi/2$ radians ( $90^{\circ}$ ).

因此，选择从 0 弧度（ $0^{\circ}$ ）到 $\pi/2$ 弧度（ $90^{\circ}$ ）的第一个四分之一周期是可以接受的。

$V_{rms}$ is the value indicated by the vast majority of AC voltmeters.

$V_{rms}$ 是绝大多数交流电压表显示的值。

It is the value that, when applied across a resistance, produces the same amount of heat that a direct current (DC) voltage of the same magnitude would produce.

当这个值施加在电阻两端时，它产生的热量与相同大小的直流（DC）电压产生的热量相同。

For example, 1 V applied across a 1 $\Omega$ resistor produces 1 W of heat.

例如，1 伏电压施加在 1 欧姆的电阻上会产生 1 瓦的热量。

A 1 $V_{rms}$ sinewave applied across a 1 $\Omega$ resistor also produces 1 W of heat.

一个 1 $V_{rms}$ 的正弦波施加在 1 欧姆的电阻上也会产生 1 瓦的热量。

That 1 $V_{rms}$ sinewave has a peak voltage of $\sqrt{2}$ V ( $\approx$ 1.414 V), and a peak - to - peak voltage of 2 $\sqrt{2}$ V ($\approx$2.828 V).

那个 1 $V_{rms}$ 的正弦波峰值电压为 $\sqrt{2}$ 伏（约 1.414 伏），峰 - 峰值电压为 2 $\sqrt{2}$ 伏（约 2.828 伏）。

Since finding a full derivation of the formulas for root - mean - square ( $V_{rms}$ ) voltage is difficult, it is done here for you.

由于完整推导均方根（ $V_{rms}$ ）电压的公式比较困难，这里为你进行推导。

$\large \begin{align*} V_{rms(sinewave)}&=\sqrt{\frac{1}{\pi/2}\int_{0}^{\pi/2}(V_{pk}\sin\theta)^2d\theta}\\ &=\sqrt{\frac{2\cdot V_{pk}^2}{\pi}\left(\frac{\theta}{2}-\frac{1}{4}\sin(2\theta)\right)\big|_{0}^{\pi/2}}\\ &=\frac{\sqrt{2}\cdot V_{pk}}{\sqrt{\pi}}\sqrt{\left(\frac{\pi/2}{2}-\frac{1}{4}\sin(\pi)\right)-\left(\frac{0}{2}-\frac{1}{4}\sin(0)\right)}\\ &=\frac{\sqrt{2}\cdot V_{pk}}{\sqrt{\pi}}\sqrt{\left(\frac{\pi}{4}-0\right)-(0 - 0)}\\ &=\frac{\sqrt{2}\cdot V_{pk}}{\sqrt{\pi}}\cdot\frac{\sqrt{\pi}}{2}\\ &=\frac{1}{\sqrt{2}}\cdot V_{pk} \end{align*}$

So, $\large V_{rms}=\frac{1}{\sqrt{2}}\cdot V_{pk}\approx0.707V_{pk}$

$\large \frac{1}{\sqrt{2}} = 0.70710678118654752440084436210485$

$V_{rms}$ is calculated by taking the square root of the mean average of the square of the voltage in an appropriately chosen interval. For symmetrical waveforms like the sine wave, a quarter cycle faithfully represents all four quarter cycles of the waveform. Therefore, it is acceptable to choose the first quarter cycle, which goes from 0 radians ( $0^\circ$ ) through $\frac{\pi}{2}$ radians ( $90^\circ$ ).
$V_{rms}$ 是通过对在适当选择的区间内电压平方的平均值取平方根来计算的。对于像正弦波这样的对称波形，四分之一周期能如实地代表整个波形的四个四分之一周期。因此，选择从0弧度（ $0^\circ$ ）到 $\frac{\pi}{2}$ 弧度（ $90^\circ$ ）的第一个四分之一周期来计算是可行的。

$\large V_{rms} = \sqrt{\frac{1}{\frac{\pi}{2}} \int_{0}^{\frac{\pi}{2}} (V_{pk} \sin \theta)^2 \cdot d\theta}$

$V_{rms}$ is the value indicated by the vast majority of AC voltmeters. It is the value that, when applied across a resistance, produces the same amount of heat that a direct current (DC) voltage of the same magnitude would produce. For example, 1 V applied across a 1 $\Omega$ resistor produces 1 W of heat. A 1 $V_{rms}$ sine wave applied across a 1 $\Omega$ resistor also produces 1 W of heat.
$V_{rms}$ 是绝大多数交流电压表显示的值。这个值在加在电阻两端时，产生的热量与相同大小的直流电压加在该电阻上产生的热量相同。例如，1伏电压加在1欧姆的电阻上产生1瓦的热量。一个 $V_{rms}$ 为1伏的正弦波加在1欧姆的电阻上也产生1瓦的热量。

$\frac{V^2}{R}$ （用于计算功率，此处说明 $V_{rms}$ 与直流电压在产生热量上等效时涉及的功率计算）

$\large V_{rms} = \frac{1}{\sqrt{2}} V_{pk} \approx 0.707 V_{pk}$

—

The RMS value of a waveform is the DC-equivalent voltage.
波形的均方根（RMS）值是等效直流电压。

It means that if you have a sine wave with an RMS value of 10 volts RMS, in order to deliver the same power via DC voltage, you would need 10 volts DC.
这意味着，如果你有一个均方根值为 10 伏的正弦波，为了通过直流电压传递相同的功率，你需要 10 伏直流电。

Do not confuse the average magnitude with the RMS voltage; $V_{av}$ does not equal $V_{rms}$ . In fact, technically, the average voltage of an unshifted sine wave is 0 V.
不要把平均幅值和均方根电压混淆； $V_{av}$ 不等于 $V_{rms}$ 。实际上，从技术角度讲，未偏移的正弦波的平均电压为 0 伏。

2. $V_m$ （通常指峰值电压，等同于 $V_{pk}$ ）

$V_m$ generally refers to the peak/max voltage on your waveform.
$V_m$ 通常指波形上的峰值/最大电压。

在这里插入图片描述

$V_m$ is used when you want to know the max voltage of a waveform. In phasor notation, you use $V_m$ as the coefficient. When calculating power, you use RMS values.
当你想知道波形的最大电压时会用到 $V_m$ 。在相量表示法中，你将 $V_m$ 用作系数。在计算功率时，使用的是RMS值。

3. 三相电路中的应用

Regarding 3-phase circuits, there is no fundamental difference except you are calculating power three times; one for each phase.
对于三相电路，除了需要对每相分别计算功率（即计算三次）之外，没有根本区别。

If you have 3 resistors in a delta connection, the power is the RMS Line voltage squared and divided by the delta resistor to which that line voltage is across. Repeat for the two other line voltages and sum all three.
如果有3个电阻采用三角形连接，那么功率为线电压的 RMS 值的平方除以该线电压所跨接的三角形电阻。对另外两个线电压重复此计算，然后将三者相加。

$P_1 = \frac{V_{L - rms}^2}{R_1}$ （ $P_1$ 为一相功率， $V_{L - rms}$ 为线电压的 RMS 值， $R_1$ 为对应电阻，另外两相类似计算）

If you have resistors in star-formation, you must use the phase RMS voltage (line divided by $\sqrt{3}$ ) and calculate the 3 individual powers. Add them together to get the total power.
如果电阻采用星形连接，你必须使用相电压的 RMS 值（线电压除以 $\sqrt{3}$ ）来计算三相各自的功率，然后将它们相加得到总功率。

$V_{p - rms} = \frac{V_{L - rms}}{\sqrt{3}}$ （ $V_{p - rms}$ 为相电压的RMS值， $V_{L - rms}$ 为线电压的RMS值）；

$P_p = \frac{V_{p - rms}^2}{R_p}$ （ $P_p$ 为一相功率， $R_p$ 为对应相电阻）

If the loads are imbalanced and there is no neutral connection, then there is more math, but I hope you get the picture.
如果负载不平衡且没有中性线连接，那么计算会更复杂，但希望你能理解大致情况。

summary

RMS（均方根值）

RMS 常用于表示交流电压或电流的有效值。从热效应角度来看，让交流电和直流电分别通过相同阻值的电阻，如果在相同时间内它们产生的热量相等，那么就把这个直流电的数值叫做该交流电的有效值，它能很好地反映交流电压或电流在电路中产生功率的能力，例如在计算交流电路中的功率、分析电路元件的发热等问题时，有效值都是非常重要的参数。

峰值（Peak Value）

峰值就是交流信号在一个周期内所能达到的最大值，比如正弦交流电的表达式 $I_m\sin(\omega t+\varphi)$ 中， $I_m$ 就是电流的峰值。

直流电路与交流电路功率计算

直流电路

在直流电路中，欧姆定律表达式为 $\frac{V}{R}$ ，由此可推出 $V = I R$ 。功率公式为 $P = V I$ ，将 $V = I R$ 代入功率公式可得 $P = I^{2}R$ ；若将 $\frac{V}{R}$ 代入 $P = V I$ ，则得到 $\frac{V^{2}}{R}$ 。这些公式在已知直流电压 $V$ 、电流 $I$ 和电阻 $R$ 中的任意两个量时，能准确计算出电路消耗的功率。

交流电路

单相交流电路

交流电路中，由于电压和电流随时间变化，功率计算需考虑有效值（RMS 值）。以正弦交流电为例，其有功功率 $UI\cos\varphi$ ，无功功率 $UI\sin\varphi$ ，视在功率 $S = U I$ 。

$U$ 、 $I$ 均指有效值， $\cos\varphi$ 为功率因数， $\sin\varphi$ 为无功功率因数，且满足 $S^{2} = P^{2} + Q^{2}$ 。

三相交流电路

三角形连接

在三相电路的三角形连接中，线电压 $U_{L}$ 等于相电压 $U_{P}$ ，线电流 $I_{L}$ 是相电流 $I_{P}$ 的 $\sqrt{3}$ 倍，即 $U_{L}=U_{P}$ ， $I_{L}=\sqrt{3}I_{P}$ ， $U_{L}$ 、 $I_{L}$ 、 $U_{P}$ 、 $I_{P}$ 均为有效值。其功率计算通常基于线电压 $U_{L}$ 和线电流 $I_{L}$ ，公式为 $P=\sqrt{3}U_{L}I_{L}\cos\varphi$ 。也可用相电压和相电流表示为 $3U_{P}I_{P}\cos\varphi$ ，由于 $U_{L}=U_{P}$ 和 $I_{L}=\sqrt{3}I_{P}$ ，所以 $3U_{P}I_{P}\cos\varphi=\sqrt{3}U_{L}I_{L}\cos\varphi$ 。

星形连接

在三相电路的星形连接中，线电压 $U_{L}$ 是相电压 $U_{P}$ 的 $\sqrt{3}$ 倍，线电流 $I_{L}$ 等于相电流 $I_{P}$ ，即 $U_{L}=\sqrt{3}U_{P}$ ， $I_{L}=I_{P}$ ，各量均为有效值。功率计算基于相电压 $U_{P}$ 和相电流 $I_{P}$ ，也可根据线电压和线电流来计算功率，公式是 $P=\sqrt{3}U_{L}I_{L}\cos\varphi$ 。同样能用相电压和相电流表示为 $3U_{P}I_{P}\cos\varphi$ ，由于 $U_{L}=\sqrt{3}U_{P}$ 和 $I_{L}=I_{P}$ ，所以 $3U_{P}I_{P}\cos\varphi=\sqrt{3}U_{L}I_{L}\cos\varphi$ 。

负载平衡与不平衡

平衡三相电路

在平衡三相电路中，各相电压和电流大小相等，相位差为 $120^{\circ}$ 。此时可直接使用上述公式计算总功率。对于三角形连接，功率 $P=\sqrt{3}U_{L}I_{L}\cos\varphi$ ；对于星形连接，功率 $P=\sqrt{3}U_{L}I_{L}\cos\varphi$ 或 $3U_{P}I_{P}\cos\varphi$ 。

不平衡三相电路

在三相电路中，若负载不平衡，无论有无中性连接，各相电流和电压的大小和相位关系都会变得复杂，不能简单按平衡负载时的方法计算。需分别计算各相功率，然后相加得到总功率，公式为 $P_{总}=P_{A}+P_{B}+P_{C}=U_{A}I_{A}\cos\varphi_{A}+U_{B}I_{B}\cos\varphi_{B}+U_{C}I_{C}\cos\varphi_{C}$ ，其中 $U_{A}$ 、 $I_{A}$ 、 $\varphi_{A}$ 等分别为各相的电压、电流及功率因数。