LaTeX 中上下标相关命令的使用规则

注：本文为 LaTeX 中上下标相关命令使用文章合辑。

英文引文，机翻未校。

---

LaTeX 中上下标及相关命令的使用规则

引言

本文档旨在详细介绍在 LaTeX 中使用上下标以及相关命令的规则和技巧。掌握这些规则对于编写清晰、准确的数学公式至关重要。

基本上下标规则

在 LaTeX 中，上下标的基本运算符分别是 ^（表示上标）和 _（表示下标）。通常情况下，上标显示在符号的右上角，下标显示在符号的右下角。

基本语法

a_{10}^{20}

显示效果为：

$a_{10}^{20}$

如果上下标的内容是单个字符，可以省略花括号。例如，a^2 和 a_1。

如果上下标内容包含多个字符，则必须使用花括号将它们括起来。

上下标可以同时使用

LaTeX 代码	打印效果
a_1^2	$a_1^2$
a^2_1	$a_1^2$
{a^2}_1	${a^2}_1$
{a_1}^2	${a_1}^2$

数学运算符的上下标显示规则

数学运算符（如求和符号 \sum、积分符号 \int 等）的上下标显示位置在段内和段外环境中有所不同。

段外环境

在段外环境（例如使用 displaymath 环境或双美元符号 $$）中，数学运算符的上下标默认显示在运算符的正上方和正下方。

\begin{displaymath}
\sum_a^b
\end{displaymath}

显示效果为：

$$\sum _a^b$$

段内环境

在段内环境（使用单美元符号 $）中，默认情况下，上下标显示在运算符的右上角和右下角。

$\sum_a^b$

显示效果为：

${\sum }_a^b$

使用 \limits 强制显示位置

若希望在段内环境中，数学运算符的上下标也显示在正上方和正下方，可以使用 \limits 命令。

$\sum \limits_a^b$

显示效果为：

$$\sum _a^b$$

使用 \nolimits 强制显示在角标位置

与之相对，可以使用 \nolimits 强制让角标显示在角标位置。

$\sum \nolimits_a^b$

显示效果为：

$${\sum }_a^b$$

非数学运算符的上下标显示

对于非数学运算符的普通符号，若希望其上下标显示在正上方和正下方，不能直接使用 \limits 命令。可以借助 \mathop 命令，使普通符号具备类似数学运算符的特性。

$\mathop{x} \limits_a^b$

显示效果为：

$$\underset{a}{\overset{b}{x}}$$

多行上下标

在数学运算符上放置多行上下标时，可以使用 \substack 命令。该命令需要包含在花括号内，并使用双反斜杠 \\ 分隔行。

\sum_{\substack{i=1 \\ i \neq j}}^{n}

显示效果为：

$$\sum _{\begin{array}{c}i=1\\ i\ne j\end{array}}^n$$

\stackrel 命令的使用

基本语法

\stackrel 命令用于在一个符号上方放置另一个符号或表达式，常用于表示极限、关系或箭头上的文字等。其基本语法为：

\stackrel{上标}{下标}

其中，上标 会显示在 下标 的正上方。

\stackrel{a}{b}

显示效果为：

$$\stackrel{a}{b}$$

示例

A \stackrel{f}{\rightarrow} B

显示效果为：

$$A\stackrel{f}{\to }B$$

\stackrel 与 \limits 的区别

• \stackrel：用于在符号上方放置一个表达式，通常用于表示条件或标注。
• \limits：用于强制将上下标显示在符号的正上方和正下方，通常用于数学运算符。

调整上下标的位置和大小

调整上下标大小

LaTeX 默认会自动调整上下标的大小，但有时需要手动调整以获得更好的显示效果。

使用 \scriptstyle 和 \scriptscriptstyle 命令

• \scriptstyle：用于设置一级上下标的大小。
• \scriptscriptstyle：用于设置二级上下标的大小。

A_{\scriptstyle b} \quad A_{\scriptscriptstyle c}

显示效果为：

$$A_b{A}_c$$

使用 \text 命令结合字体大小命令

可以使用 \text 命令结合 LaTeX 的字体大小命令（如 \tiny、\scriptsize、\footnotesize 等）来更灵活地控制上下标的大小。

A_{\text{\tiny b}} \quad A_{\text{\scriptsize c}}

显示效果为：

$$A_{\text{b}}{A}_{\text{c}}$$

使用 \scalebox 命令

\scalebox 命令可以缩放任何内容，包括上下标。这提供了精确控制大小的方法。需要引入 graphicx 包。

全局设置上下标大小

可以在导言区使用 \DeclareMathSizes 命令来全局设置不同数学环境下的字体大小。这会影响整个文档中上下标的大小。

语法：\DeclareMathSizes{正文字符大小}{正常数学字符大小}{一级上下标大小}{二级上下标大小}

例如：

\DeclareMathSizes{10}{10}{7}{5}

这表示正文字符大小为 10pt，正常数学字符大小为 10pt，一级上下标大小为 7pt，二级上下标大小为 5pt。注意：这个设置需要在文档开始之前（即在导言区）进行。

使上下标保持相同大小的方法

有时需要确保上下标具有相同的大小，可以使用以下方法：

使用 \scriptstyle 命令

可以通过在上下标中显式地使用 \scriptstyle 命令来强制上下标保持相同的大小。

A^{\scriptstyle b} \quad A_{\scriptstyle c}

显示效果为：

$$A^b{A}_c$$

使用 \text 命令结合字体大小命令

可以使用 \text 命令结合 LaTeX 的字体大小命令。

A^{\text{\scriptsize b}} \quad A_{\text{\scriptsize c}}

显示效果为：

$$A^{\text{b}}{A}_{\text{c}}$$

使用 \raisebox 命令提升（或降低）插入的内容（如文本、图像等）的位置

该命令可以用于调整垂直位置，使内容相对于周围内容上下移动。

语法如下：

\raisebox{<distance>}[<height>][<depth>]{<content>}

其中：

• 表示要上升（正值）或下降（负值）的距离。
• 表示内容的高度。
• 表示内容的深度。
• 是要调整位置的内容。
  例如，\raisebox{2pt}{内容} 将内容向上移动 2 点。

可以根据需要使用 \raisebox 命令来调整文本或图像的垂直位置，使其与周围内容对齐或居中。

总结

功能	命令	说明
基本上下标	^ 和 _	使用 ^ 设置上标，使用 _ 设置下标。
数学运算符上下标位置	\limits	在段内使用数学运算符时，使上下标显示在正上方和正下方。
普通符号上下标	\mathop	使普通符号具有数学运算符特性，上下标显示在正上方和正下方。
普通符号上下标位置调整	\raisebox	调整普通符号上下标的垂直位置。
多行上下标	\substack	在数学运算符上放置多行上下标。
上下标中包含文本	\text	在数学模式下将文本插入上下标。
上下标大小调整	\scriptstyle、\scriptscriptstyle、\text、\scalebox	调整上下标的大小。
全局上下标大小设置	\DeclareMathSizes	对全局上下标大小进行统一设置。

选择合适的方法取决于具体的需求和期望的显示效果。

---

讨论

Differences between \stackrel and \stackbin

What are the differences between \stackrel and \stackbin? In what situations is it better to use one or the other?
\stackrel 和 \stackbin 之间有什么区别？在哪些情况下使用其中一个会更好呢？

edited Dec 24, 2011 at 3:59

Werner♦）

asked Dec 24, 2011 at 3:24

Village

• 5
  Effectively, this boils down to the question related to \mathbin and \mathrel which can be found in what is the difference between mathbin vs. mathrel
  实际上，这可以归结为与 \mathbin 和 \mathrel 相关的问题，该问题可以在“\mathbin 与 \mathrel 之间的区别是什么”中找到。

– percusse）

CommentedDec 24, 2011 at 3:36

• Which do I use if I just want to stack text and do not want added spacing to separate math from text?
  如果我只是想堆叠文本，并且不希望添加额外的间距来分隔数学内容和文本，我应该使用哪一个呢？

– Village

CommentedDec 24, 2011 at 3:42

• @Village: If you want to remove any text influence from your \stackrel (or \stackbin) choice, then you can use \usepackage{amsmath,stackrel}KaTeX parse error: Undefined control sequence: \makebox at position 18: …stackrel{\text{\̲m̲a̲k̲e̲b̲o̲x̲[0pt]{abc}}}{=}…. This typesets abc in text mode in the appropriate font size without any width, and would therefore not influence math spacing. \stackrel and \stackbin typically only have narrow entries on top of/below them. Is this what you might be after?
  @Village：如果你想在选择 \stackrel（或 \stackbin）时消除任何文本的影响，那么你可以使用 \usepackage{amsmath,stackrel} 并输入 $a\stackrel{\text{\makebox[0pt]{abc}}}{=}b$。这会以合适的字体大小在文本模式下排版 abc，并且没有任何宽度，因此不会影响数学排版的间距。\stackrel 和 \stackbin 通常在其上方/下方只有较窄的内容。这是你想要的吗？

– Werner♦

CommentedDec 24, 2011 at 4:05

• Yes, I just want three layers of stacked and centered text, without modifying any of the spacing. Would it be better if I used some other way to position the text in three levels?
  是的，我只是想要三层堆叠且居中的文本，并且不修改任何间距。如果我使用其他一些方法来将文本定位为三层，会不会更好呢？

– Village

CommentedDec 24, 2011 at 4:28

• @Village: You could use any number of means. For example, typeset things in an array or tabular that is vertically centered, or use \stackrel. Either way, this seems to be a departure from your current question which relates specifically to \stackrel and \stackbin.
  @Village：你可以使用多种方法。例如，在垂直居中的 array 或 tabular 环境中排版内容，或者使用 \stackrel。无论哪种方式，这似乎都偏离了你当前的问题，你当前的问题具体是关于 \stackrel 和 \stackbin 的。

– Werner♦

CommentedDec 24, 2011 at 4:45

3 Answers

Without the stackrel package, \stackrel is defined in ltxmath.dtx as
如果没有 stackrel 宏包，\stackrel 在 ltxmath.dtx 中被定义为

\def\stackrel#1#2{\mathrel{\mathop{#2}\limits^{#1}}}

which typesets a relational operator with a top limit (effectively placing it on top). Heiko Oberdiek’s stackrel package is said to provide an
它排版一个带有上限的关系运算符（实际上是将其放置在上方）。据说 Heiko Oberdiek 的 stackrel 宏包 提供了一个

Enhancement to the \stackrel command.
对 \stackrel 命令的增强。

This “enhancement” provides an optional argument to \stackrel for placing something below the relational operator (using a similar process as the original \stackrel). Additionally, it provides a counterpart for binary relations called \stackbin. The difference between the two (or when to use which one) is contained within the post What is the difference between \mathbin vs. \mathrel? Here is a similar take on the use of stackrel.
这种“增强”为 \stackrel 提供了一个可选参数，用于在关系运算符下方放置某些内容（使用与原始 \stackrel 类似的过程）。此外，它还为二元关系提供了一个对应的命令 \stackbin。这两者之间的区别（或者何时使用哪一个）包含在帖子 “\mathbin 与 \mathrel 之间的区别是什么？” 中。这里是关于 \stackrel 使用的类似说明。

\documentclass{article}
\usepackage{stackrel}
\begin{document}
\begin{tabular}{clc}
  \multicolumn{3}{c}{Relations} \\[5pt]
  \LaTeX & Typeset & width \\
  \hline
  \verb|$x=x$| & $x=x$ & \setbox0=\hbox{$x=x$} \the\wd0 \\
  \verb|$x\stackbin[c]{a}{=}x$| & $x\stackbin[c]{a}{=}x$ & 
    \setbox0=\hbox{$x\stackbin[c]{a}{=}x$} \the\wd0 \\
  \verb|$x\stackrel[c]{a}{=}x$| & $x\stackrel[c]{a}{=}x$ & 
    \setbox0=\hbox{$x\stackrel[c]{a}{=}x$} \the\wd0 \\[10pt]
  \multicolumn{3}{c}{Binary operators} \\[5pt]
  \LaTeX & Typeset & width \\
  \hline
  \verb|$x+x$| & $x+x$ & \setbox0=\hbox{$x+x$} \the\wd0 \\
  \verb|$x\stackbin[c]{a}{+}x$| & $x\stackbin[c]{a}{+}x$ & 
    \setbox0=\hbox{$x\stackbin[c]{a}{+}x$} \the\wd0 \\
  \verb|$x\stackrel[c]{a}{+}x$| & $x\stackrel[c]{a}{+}x$ & 
    \setbox0=\hbox{$x\stackrel[c]{a}{+}x$} \the\wd0
\end{tabular}
\end{document}

Note the equivalent spacing using \stackrel with =, while similar spacing is returned using \stackbin and +. In essence, use \stackrel for relational operators, and \stackbin for binary operators.
请注意，使用 \stackrel 与 = 时的间距是相等的，而使用 \stackbin 与 + 时返回的间距是相似的。本质上，对于关系运算符使用 \stackrel，对于二元运算符使用 \stackbin。

edited Apr 13, 2017 at 12:35

1

answered Dec 24, 2011 at 3:56

Werner♦

• why do you use $x=x$ & \setbox0=\hbox{$x=x$} \the\wd0 instead of \setbox0=\hbox{$x=x$} \usebox0 & \the\wd0 ?
  你为什么使用 $x=x$ & \setbox0=\hbox{$x=x$} \the\wd0 而不是 \setbox0=\hbox{$x=x$} \usebox0 & \the\wd0 呢？

– user2987828

CommentedMar 2, 2017 at 12:54

• @user2987828: No particular reason. The storing to a box and measuring occurs in the same cell.
  @user2987828：没有特别的原因。将内容存储到盒子中以及测量是在同一个单元格中进行的。

– Werner♦

CommentedMar 2, 2017 at 16:18

130

Don’t use \stackrel or \stackbin, they are obsolete. Use instead \underset and \overset from amsmath as they automatically space things correctly (whether it’s a binary relation or a binary operator):
不要使用 \stackrel 或 \stackbin，它们已经过时了。而是使用来自 amsmath 宏包的 \underset 和 \overset，因为它们会自动正确地设置间距（无论是对于二元关系还是二元运算符）：

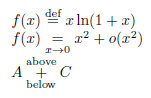
\documentclass{article}
\usepackage{amsmath}
\begin{document}
$f(x) \overset{\text{def}}{=} x \ln(1+x)$
$f(x) \underset{x \to 0}{=} x^2 + o(x^2)$
$A \underset{\text{below}}{\overset{\text{above}}{+}} C$
\end{document}

$$f(x)\stackrel{\text{def}}{=}x\ln (1+x)$$

$$f(x)\underset{x\to 0}{=}{x}^2+o(x^2)$$

$$A\underset{\text{below}}{\stackrel{\text{above}}{+}}C$$

answered Dec 24, 2011 at 7:43

Philippe Goutet

• Can you please add a reference which clearly shows that and why \stack* is obsolete?
  你能添加一个参考资料，清楚地说明 \stack* 为什么以及如何过时的吗？

– ManuelSchneid3r

CommentedFeb 5, 2021 at 11:51

2
@ManuelSchneid3r: you’re not going to find a better reason than the one I gave in my post (manual spacing vs automatic spacing). I should also have mentioned \overunderset that puts something both above and below the symbol (and would have simplified my third example).
@ManuelSchneid3r：你不会找到比我在帖子中给出的更好的理由了（手动设置间距与自动设置间距）。我还应该提到 \overunderset，它可以在符号的上方和下方都放置内容（并且会简化我的第三个例子）。

– Philippe Goutet

CommentedFeb 8, 2021 at 9:09

I personally prefer using \mathop, because it’s simpler. Instead of using nested under/oversets, you could simply write:
我个人更喜欢使用 \mathop，因为它更简单。与其使用嵌套的 \underset 和 \overset，你可以简单地写成：

$A \mathop{+}_{\text{below}}^{\text{above}} C$

$A{+}_{\text{below}}^{\text{above}}C$

answered Jun 5, 2014 at 8:31

Sparkler

4

That works if you wrap it in \displaystyle{} ; otherwise (inline mode) it behaves like \Sum etc. and puts the text on the right as superscript / subscript.
如果你将其用 \displaystyle{} 包裹起来，它就可以正常工作；否则（在行内模式下），它的行为就像 \Sum 等一样，并且会将右边的文本作为上标/下标。

– Frentos

CommentedMar 14, 2018 at 19:09

You can use $A\underset{\text{below}}{\overset{\text{above}}{+}}C$ in inline mode.
你可以在行内模式下使用 $A \mathop{+}\limits_{\text{below}}^{\text{above}} C$。

– VicaYang
（用户名：VicaYang）

CommentedMay 26, 2021 at 8:14
于2021年5月26日8点14分评论

---

What is the difference between \mathbin vs. \mathrel?

\mathbin 与 \mathrel 之间的区别是什么？

These seem to be very similar as they both separate two operands. When would one be used over the other? Is there any difference in the math spacing surrounding them?
它们看起来非常相似，因为它们都用于分隔两个操作数。什么时候应该使用其中一个而不是另一个呢？它们周围的数学排版间距有什么不同吗？

How would the spacing in these relate to to the spacing produced by \mathop?
这些间距与 \mathop 产生的间距有什么关系呢？

edited Dec 21, 2011 at 6:48

Werner♦

asked Dec 21, 2011 at 5:49

Commented Nov 7, 2012 at 10:40

2 Answers

From the name, \mathbin modifies the spacing around something so that it adheres to that of a binary operator, while \mathrel modifies the spacing to denote that of a binary relation. Here is an elementary approach at showcasing the difference:
从名称上看，\mathbin 修改围绕某个内容的间距，使其符合二元 运算符 的间距规则，而 \mathrel 修改间距以表示二元 关系 的间距规则。这里是展示这种区别的一个基本方法：

\documentclass{article}
\begin{document}
\begin{tabular}{clc}
  \multicolumn{3}{c}{Relations} \\[5pt]
  \LaTeX & Typeset & width \\ \hline
  \verb|$x=x$| & $x=x$ & \setbox0=\hbox{$x=x$} \the\wd0 \\
  \verb|$x\mathbin{=}x$| & $x\mathbin{=}x$ & \setbox0=\hbox{$x\mathbin{=}x$} \the\wd0 \\
  \verb|$x\mathrel{=}x$| & $x\mathrel{=}x$ & \setbox0=\hbox{$x\mathrel{=}x$} \the\wd0 \\[10pt]
  \multicolumn{3}{c}{Binary operators} \\[5pt]
  \LaTeX & Typeset & width \\ \hline
  \verb|$x+x$| & $x+x$ & \setbox0=\hbox{$x+x$} \the\wd0 \\
  \verb|$x\mathbin{+}x$| & $x\mathbin{+}x$ & \setbox0=\hbox{$x\mathbin{+}x$} \the\wd0 \\
  \verb|$x\mathrel{+}x$| & $x\mathrel{+}x$ & \setbox0=\hbox{$x\mathrel{+}x$} \the\wd0
\end{tabular}
\end{document}

Note the spacing around + matching that of \mathbin, while the spacing around = matches that of \mathrel.
请注意，+ 周围的间距与 \mathbin 的间距匹配，而 = 周围的间距与 \mathrel 的间距匹配。

From the TeXBook (Chapter 17: More about Math, p 154-):

Every math character is given an identifying code number between 0 and 4095, obtained by adding 256 times the family number to the position number. This is easily expressed in hexadecimal notation, using one hexadecimal digit for the family and two for the character; for example, \hex{24A} stands for character \hex{4A} in family 2. Each character is also assigned to one of eight classes, numbered 0 to 7, as follows:
每个数学字符都被赋予一个介于 0 到 4095 之间的识别码，通过将族编号乘以 256 再加上位置编号得到。这很容易用十六进制表示，用一个十六进制数字表示族，用两个十六进制数字表示字符；例如，\hex{24A} 表示族 2 中的字符 \hex{4A}。每个字符也被分配到八个类别之一，编号从 0 到 7，如下所示：

type	symbol	类型
Class 0: Ordinary	/	普通
Class 1: Large operator	\sum	大型运算符
Class 2: Binary operation	+	二元运算
Class 3: Relation	=	关系
Class 4: Opening	(	左括号
Class 5: Closing	)	右括号
Class 6: Punctuation	,	标点符号
Class 7: Variable family	x	变量族

Classes 0 to 6 tell what “part of speech” the character belongs to, in math-printing language; class 7 is a special case […]. The class number is multiplied by 4096 and added to the character number, and this is the same as making it the leading digit of a four-digit hexadecimal number.
类别 0 到 6 说明了在数学排版语言中字符属于什么“词性”；类别 7 是一个特殊情况[…]。类别编号乘以 4096 并加到字符编号上，这与将其作为一个四位十六进制数的首位数字是一样的。
…
TeX associates classes with subformulas as well as with individual characters. Thus, for example, you can treat a complex construction as if it were a binary operation or a relation, etc., if you want to. The commands \mathord, \mathop, \mathbin, \mathrel, \mathopen, \mathclose, and \mathpunct are used for this purpose; each of them is followed either by a single character or by a subformula in braces. For example, \mathopen\mathchar"1234 is equivalent to \mathchar"4234, because \mathopen forces class 4 (opening). In the formula $G\mathbin:H$, the colon is treated as a binary operation.
…
TeX 将类别与子公式以及单个字符相关联。因此，例如，如果你愿意，你可以将一个复杂的结构当作二元运算或关系等来处理。命令 \mathord、\mathop、\mathbin、\mathrel、\mathopen、\mathclose 和 \mathpunct 就是用于这个目的；它们中的每一个后面要么跟着一个单个字符，要么跟着一个用花括号括起来的子公式。例如，\mathopen\mathchar"1234 等价于 \mathchar"4234，因为 \mathopen 强制类别为 4（左括号）。在公式 $G\mathbin:H$ 中，冒号被当作二元运算处理。
…
There’s also an eighth classification, \mathinner, which is not normally used for individual symbols; fractions and \left...\right constructions are treated as “inner” subformulas, which means that they will be surrounded by additional space in certain circumstances. All other subformulas are generally treated as ordinary symbols, whether they are formed by \overline or \hbox or \vcenter or by simply being enclosed in braces. Thus, \mathord isn’t really a necessary part of the TeX language; instead of typing $1\mathord,234$ you can get the same effect from $1{,}234$.
还有第八种分类 \mathinner，它通常不用于单个符号；分数和 \left...\right 结构被当作“内部”子公式处理，这意味着在某些情况下它们会被额外的间距包围。所有其他子公式通常都被当作普通符号处理，无论它们是由 \overline 或 \hbox 或 \vcenter 形成的，还是仅仅用花括号括起来的。因此，\mathord 并不是 TeX 语言中真正必要的部分；与其输入 $1\mathord,234$，你可以通过输入 $1{,}234$ 得到相同的效果。

edited Mar 20, 2017 at 19:16

David Carlisle

answered Dec 21, 2011 at 6:08

Werner♦

• Most lists I have seen does not include class 7, but treats alphanumeric characters as ordinary. Why is it different here?
  我见过的大多数列表都不包括类别 7，而是将字母数字字符当作普通字符处理。为什么这里不同呢？

– Gaussler

CommentedJul 16, 2015 at 18:57

• @Gaussler: Class 7 indeed behaves the same as class 0 with regards to spacing. The difference is in what font the character is taken from.
  @Gaussler：就间距而言，类别 7 的行为确实与类别 0 相同。区别在于字符所使用的字体。

– Emil Jeřábek

CommentedFeb 18, 2016 at 18:29

There are three main differences between \mathrel and \mathbin:
\mathrel 和 \mathbin 之间有三个主要区别：

1. For optimal readability of math formulas, the more important elements must receive more space. That’s why \mathrel (for math relations like =, <, > etc.) receives a thick space (5/18th of an em) while \mathbin (for math binary operators like +, -, \oplus etc.) receives a medium space (4/18th of an em). The difference is subtle, but enhances reading of formulas.
为了使数学公式具有最佳的可读性，更重要的元素必须有更多的间距。这就是为什么 \mathrel（用于像 =, <, > 等数学关系）会有一个较宽的间距（1 em 的 5/18），而 \mathbin（用于像 +, -, \oplus 等数学二元运算符）会有一个中等的间距（1 em 的 4/18）。这种区别很微妙，但提高了公式的可读性。

2. \mathbin and \mathrel behave differently relative to shrinking or stretching. When TeX does not have enough space available on a given line, it will contract a \mathbin space while it will never do so for a \mathrel space. When TeX has too much space available on a given line, it will stretch both. Here are the values used (1mu = 1/18th em):
\mathbin 和 \mathrel 在收缩或拉伸方面的行为不同。当 TeX 在给定的一行上没有足够的空间时，它会收缩 \mathbin 的间距，而对于 \mathrel 的间距则永远不会这样做。当 TeX 在给定的一行上有太多的空间时，它会拉伸两者的间距。以下是使用的值（1mu = 1/18 em）：

\medmuskip = 4mu plus 2mu minus 4mu
\thickmuskip = 5mu plus 5mu

Here’s an example of both situations:
这里是两种情况的一个例子：

As you can see, in a shrinking situation, + has no space around it, but in stretching situations, = can extend much more than + (10/18th em vs 6/18th em).
如你所见，在收缩的情况下，+ 周围没有间距，但在拉伸的情况下，= 的伸展程度比 + 大得多（10/18 em 对比 6/18 em）。

3. Finally, \mathbin and \mathrel behave differently in different contexts. For example, $A = -B$ works as expected (no space between - and B) but $A = \mathrel{-}B$ would not:
3. 最后，\mathbin 和 \mathrel 在不同的上下文中行为不同。例如，$A = -B$ 按预期工作（- 和 B 之间没有间距），但 $A = \mathrel{-}B$ 则不行：

This is only one example of what can go wrong with the spacing if the type of the symbol is incorrect.
这只是如果符号的类型不正确，间距可能出现问题的一个例子。

Comparison to \mathop: contrary to \mathbin and \mathrel, \mathop is for things like \sum, \cos, \ln etc. and only inserts a thin space (3/18th em, no shrinking or stretching) and, just as \mathbin and \mathrel, has special spacing rules to make it spaced correctly in most context.
与 \mathop 的比较：与 \mathbin 和 \mathrel 相反，\mathop 用于像 \sum, \cos, \ln 等这样的情况，并且只插入一个较窄的间距（1 em 的 3/18，不收缩或拉伸），并且和 \mathbin 以及 \mathrel 一样，有特殊的间距规则，以使其在大多数上下文中的间距正确。

edited Dec 21, 2011 at 8:02

Werner♦

answered Dec 21, 2011 at 6:51

Philippe Goutet

1
from what I recall, the spacing around \mathbin and \mathrel is “symmetric” in that it is the same before and after the symbol, while \mathop isn’t: it puts things closer to the symbol on the right. Is that correct?
据我回忆，\mathbin 和 \mathrel 周围的间距是“对称的”，即符号前后的间距是相同的，而 \mathop 不是这样：它使右边的内容更靠近符号。这是正确的吗？

– Seamus

CommentedDec 21, 2011 at 17:29

4
The spacing around symbols depends on the objects which are around; for example between a mathop and an opening there’s no space (compare \log x and \log(xy)).
符号周围的间距取决于其周围的对象；例如，在一个 mathop（如 \log）和一个左括号之间没有间距（比较 \log x 和 \log(xy)）。

– egreg

CommentedDec 21, 2011 at 19:06

---

What’s the right space to right the alignment of a right aligned align environment？

右对齐环境的对齐方式的正确空间是多少？
22
As Hilbert would have put it, had he lived in the TeX-era:
正如希尔伯特所说，如果他生活在 TeX 时代：

No one shall expel us from the Paradise that AMS has created.
没有人可以把我们驱逐出 AMS 创造的天堂。
and one aspect of that paradise is release from the tyranny of eqnarray by use of the magnificent align environment (and its siblings).
而那个天堂的一个方面是通过使用宏伟的 align 环境（及其兄弟姐妹）从 eqnarray 的暴政中解脱出来。
One feature of the align environment is that it saves us considerable time and effort by only requiring one alignment character in, for example,
align 环境的一个特点是，它为我们节省了大量的时间和精力，例如，它只需要一个对齐字符。

\begin{align*}
x &= y + z \\
a &= b + c
\end{align*}

and all the spaces are just right.
而且所有的空间都恰到好处。
But just occasionally I want to align things by the other side of the relation sign. And then the automatic spacing doesn’t work:
但只是偶尔我想通过关系符号的另一侧对齐。然后自动间距不起作用：

\documentclass{article}
\usepackage{amsmath}
\begin{document}
\[
x = y + z
\]
\begin{align*}
x &= y + z
\end{align*}
\begin{align*}
x =& y + z
\end{align*}
\end{document}

Clearly, I can just add the right amount of space. But equally clearly there’s a right amount of space to be added. What is it?
显然，我可以添加适量的空间。但同样明显的是，有适量的空间可以添加。这是什么？
edited Jun 10, 2017 at 11:17
Moriambar
asked Nov 7, 2012 at 10:08
Andrew Stacey

Isn’t it just x ={}& y + z? Or am I missing something? Great title BTW.
不就是 x ={}& y + z 吗？还是我错过了什么？ 顺便说一句，很棒的标题。
– Peter Grill
Commented Nov 7, 2012 at 10:11

@PeterGrill That is it! Evidently me that was missing something.
@PeterGrill 就是这样！显然我错过了什么。

– Andrew Stacey
Commented Nov 7, 2012 at 10:22
(I’m still curious as to the right amount of spacing, though.)
（不过，我仍然很好奇合适的间距。）
– Andrew Stacey
Commented Nov 7, 2012 at 10:22

The missing space is \mskip\thickmuskip, the space TeX inserts between a Rel and an Ord atom. Writing ={} automatically supplies it, because any subformula (even an empty one) is considered as an Ord atom.
缺少的空格是 \mskip\thickmuskip，即 TeX 在 Rel 和 Ord 原子之间插入的空间。编写 ={} 会自动提供它，因为任何子公式（即使是空的）都被视为 Ord 原子。
– egreg
Commented Nov 7, 2012 at 10:34
1
@egreg That looks awfully like an answer. If you feel it is a bit short, you could add (a link/reference to - is it in TeXbyTopic?) a list of the spaces that TeX inserts between the various elements.
@egreg 这看起来非常像一个答案。如果你觉得它有点短，你可以添加 （一个链接/引用 - 它在 TeXbyTopic 中吗？) TeX 在各种元素之间插入的空格列表。
– Andrew Stacey
Commented Nov 7, 2012 at 10:37
Show 2 more comments

1 Answer

In order to understand why a space is missing, one needs to know a bit how TeX deals with formulas and what spacings it inserts between objects.
为了理解为什么缺少空格，需要了解 TeX 如何处理公式以及它在对象之间插入的间距。
First of all, TeX dismantles a formula into a sequence of math atoms, which can be of thirteen types
首先，TeX 将公式分解为数学原子序列，该序列可以是 13 种类型

Ord Op Bin Rel Open Close Punct Inner
Over Under Acc Rad Vcent
The atoms in the second line are actually considered as Ord atoms as far as spacing is concerned. For instance, $a+b=c$ becomes the sequence
就间距而言，第二行中的原子实际上被认为是 Ord 原子。例如，$a+b=c$ 成为序列

Ord Bin Ord Rel Ord
Then TeX inserts spaces according to the following table, where rows and columns are indexed with numbers: 0 = Ord, 1 = Op, 2 = Bin, 3 = Rel, 4 = Open, 5 = Close, 6 = Punct, I = Inner
然后 TeX 根据下表插入空格，其中行和列用数字索引：0 = Ord， 1 = Op， 2 = Bin， 3 = Rel， 4 = Open， 5 = Close， 6 = Punct， I = Inner

(The table is from my paper [“Simboli matematici in TeX e LaTeX”, ArsTeXnica 8 (2009), pp. 7–24](http://www.guitex.org/home/images/ArsTeXnica/AT008/Simboli matematici in TEX e LATEX.pdf); it’s an unabridged version of a similar table in the TeXbook). You find the left atom in the row and the right atom in the columns; then the number you find is interpreted as
（该表格来自我的论文 “Simboli matematici in TeX e LaTeX”，ArsTeXnica 8 （2009），第 7-24 页;这是 TeXbook 中类似表格的未删节版本)。您可以在行中找到左原子，在列中找到右原子;那么你找到的数字将被解释为

• 0 = no space 0 = 无空格
• 1 = thin space (\thinmuskip)
  1 = 狭小空间 （\thinmuskip）
• 2 = medium space (\medmuskip)
  2 = 中等间距 （\medmuskip）
• 3 = thick space (\thickmuskip)
  3 = 粗空格 （\thickmuskip）
• * = impossible combination
  * = 不可能的组合

If the number is in parentheses, then the space is inserted only if the formula (or subformula) is eventually typeset in display or text style, but not in subscript/superscript styles.
如果数字位于括号中，则仅当公式（或子公式）最终排版为显示或文本样式，而不是下标/上标样式时，才会插入空格。
Another example: the formula $(a+b)\cdot c=ac+bc$ becomes
另一个示例：公式 $(a+b)\cdot c=ac+bc$ 变为

Open Ord Bin Ord Close BIN ORD REL ORD ORD BIN ORD ORD
A subformula is anything in braces; it is eventually treated as an Ord atom.
子公式是大括号中的任何内容;它最终被视为 Ord 原子。

---

How does align guess the right spacing? When you type
align 如何猜出正确的间距？当
您键入

\begin{align*}
a &= b+c
\end{align*}

LaTeX transforms this into an alignment basically with the following template:
LaTeX 基本上使用以下模板将其转换为对齐：

\hfil $\displaystyle #$ & $\displaystyle {}#$ \hfil

where # represents the actual contents of the cell. So we have a first column with right alignment and the second column left aligned, but an empty subformula is always added before the actual contents. So the formula that’s typeset in the right column is $\displaystyle {}=b+c$ that get read as
其中 # 表示单元格的实际内容。因此，我们第一列右对齐，第二列左对齐，但总是在实际内容之前添加一个空子公式。所以右列中排版的公式是 $\displaystyle {}=b+c$，它被读作

Ord Rel Ord Bin Ord
and the spacing is just right.
而且间距恰到好处。

The same would happen with
同样的情况也会发生

\begin{align*}
a ={}& b+c \\
a=\mskip\thickmuskip & b+c
\end{align*}

Note that explicit spacing commands (or rules) do not appear in the list of atoms and are inserted along with the automatically provided spaces.
请注意，显式间距命令（或规则）不会出现在原子列表中，而是与自动提供的空格一起插入。

Abbreviations for \mskip\thinmuskip, \mskip\medmuskip and \mskip\thickmuskip are \, \: \; respectively; \! is an abbreviation fo \mskip-\thinmuskip (which can come handy for removing a thin space automatically added).
\mskip\thinmuskip、\mskip\medmuskip 和 \mskip\thickmuskip 的缩写分别为 \, \: \;;\! 是 \mskip-\thinmuskip 的缩写（在删除自动添加的细空格时可以很方便）。

One can force a single symbol or subformula to be considered as one of the above atom types by feeding it as argument to
可以通过将单个 symbol 或子公式作为参数提供给

\mathord \mathop \mathbin \mathrel \mathopen \mathclose \mathpunct \mathinner

By adding an empty subformula, you let TeX do the job which it’s paid for and don’t need to remember that table. Well, that table can come handy in some tough situation when we end up scratching our head, asking where that damn space is coming from or doesn’t show up.
通过添加一个空的子公式，你可以让 TeX 完成它所付出的工作，而不需要记住那个表格。好吧，那张桌子在一些困难的情况下会派上用场，当我们最终挠头，询问那个该死的空间从哪里来或没有出现时。
edited May 30, 2017 at 7:10
answered Nov 7, 2012 at 11:56
egreg

Brilliant (as always)! Thanks to this I will now remember that sticking a {} in is the right thing to do because now I understand what’s going on - without that remembering {} is about as easy as remembering that six times seven is forty-two.
太棒了（一如既往）！ 多亏了这一点，我现在会记住，把 {}去是正确的做法，因为现在我明白发生了什么 - 没有这个，记住 {} 就像记住 6 乘以 7 是 42 一样容易。
– Andrew Stacey
Commented Nov 7, 2012 at 12:02

Very nice! Morten Høgholm is discussing something similar in his bachelor thesis: sites.google.com/site/mortenhoegholm/breqn-thesis.pdf (See for example Table 1 on page 15.)
很好！Morten Høgholm 在他的学士论文中讨论了类似的东西：sites.google.com/site/mortenhoegholm/breqn-thesis.pdf（例如参见第 15 页的表 1。）
– Svend Tveskæg
Commented Nov 7, 2012 at 12:51

How does TeX “know” to treat the - in $-1$ as a unary rather than a binary operator – and thus not insert \medmuskip between - and 1? Is the atom type of - maybe converted “on the fly” from mathbin to mathord?
TeX 如何“知道”将 $-1$ 中的 - 视为一元而不是二进制运算符 - 从而不在 - 和 1 之间插入 \medmuskip？- 的原子类型是否可以“动态”地从 mathbin 转换为 mathord？
– Mico
Commented May 29, 2015 at 16:40
1
@Mico That’s the rule implemented by Knuth: the cases marked * in the table are declared “impossible” and the atom is turned into an ordinary one. Perhaps also the “start or end” of formula should also be treated, but, basically, an object in the Bin type with no left atom is turned into Ord: to be spaced as Bin, an object must have something compatible on either side. For instance, ”Rel Bin Ord“ is not possible and the Bin is turned into Ord. The same is for “nothing Bin Ord”; the same for “end of formula” (or subformula, of course): “Ord Bin nothing” is impossible.
@Mico 这就是 Knuth 实施的规则：表中标记为 * 的情况被宣布为“不可能”，原子被变成普通原子。也许也应该处理公式的 “start or end”，但是，基本上，Bin 类型中没有左原子的对象会变成 Ord：要以 Bin 为间隔，
对象必须在两侧都有兼容的东西。例如，“Rel Bin Ord” 是不可能的，而 Bin 变成了 Ord。“nothing Bin Ord”也是如此;“end of formula”（当然是 subformula）也是如此：“Ord Bin nothing”是不可能的。
– egreg
May 29, 2015 at 16:52

Thanks! This is a very helpful clarification of what the “impossible combination” designation entails.
谢谢！这是对 “impossible combination” 名称含义的非常有用的澄清。
– Mico
May 29, 2015 at 16:56

---

via:

• math mode - Differences between \stackrel and \stackbin - TeX
  https://tex.stackexchange.com/questions/39225/differences-between-stackrel-and-stackbin

• math mode - What is the difference between \mathbin vs. \mathrel? - TeX
  https://tex.stackexchange.com/questions/38982/what-is-the-difference-between-mathbin-vs-mathrel

• spacing - What’s the right space to right the alignment of a right aligned align environment? - TeX
  https://tex.stackexchange.com/questions/81752/whats-the-right-space-to-right-the-alignment-of-a-right-aligned-align-environme#comment174745_81752