[SMOJ2073]Bug

做法一：

枚举 $i$、$j$，考虑在结点 $i$ 和 $j$ 之间加边（令 $i<j$），如图。

图1 在结点 $i$ 和 $j$ 之间加边

加边后，可以枚举 $k$，算出从 1 到 $k$ 的最短路，得到其中的最大值，再在所有方案中取最小值，就可以得到答案。

怎么求 1 到 $k$ 的最短路呢？不妨设为 $s(k)$。

如图，我们知道，加边后，A 部分的点不受影响，仍然要用最原始的方法，从 1 走到 2，2 走到 3……从 $k-1$ 走到 $k$，即

$$s(k)=\sum_{j=1}^{k-1}w(i,i+1)\text{ if }k\leq i$$

可以发现，这部分的计算事实上可以利用前缀和进行优化。用 $f_i$表示：在原来没加边的情况下，从 1 走到 $i$ 的最短路。公式和上面是一样的，只是少了限制。

考虑 B 部分，可以发现有两种走法：最原始的方法是从 1 走到 $k$，也可以从 1 走到 $i$，再利用虫洞从 $i$ 走到 $j$，最后从 $j$ 往回走到达 $k$。考虑到 $w(i,j)=0$，有

$$s(k)=min\{f_k,f_i+(f_j-f_k)\}\text{ if }i<k<j$$

考虑 C 部分，最优方法当然是从 1 走到 $i$，从 $i$ 走到 $j$，再从 $j$ 走到 $k$，可以从 $w(i,j)=0$ 的角度理解，也可以理解为原始方法减去了中间 $i$ 到 $j$ 的部分。

图2 利用虫洞省距离的示意图

即

$$s(k)=f_k-(f_j-f_i)=f_i+(f_k-f_j)\text{ if }j\leq k$$

这样，先 $O(N)$ 预处理前缀和，再通过 $O(N^2)$ 枚举和 $O(N)$ 计算，就可以求出答案了。

时间复杂度：$O(N^3)$
期望得分：30%
参考代码：

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>

using namespace std;

const int MAXN = 1e5 + 100;

int N;
long long len[MAXN], f[MAXN];

int main(void) {
    freopen("2073.in", "r", stdin);
    freopen("2073.out", "w", stdout);
    scanf("%d", &N); f[0] = 0LL;
    for (int i = 1; i < N; i++) {
        scanf("%lld", &len[i]);
        f[i] = f[i - 1] + len[i];
    }

    long long ans = 214748364700000LL;
    for (int i = 1; i < N; i++)
        for (int j = i + 1; j <= N; j++) {
            long long m = 0;
            for (int k = 2; k <= N; k++) {
                long long c;
                if (k <= i) c = f[k - 1]; //A 部分
                else if (k < j) c = min(f[k - 1], f[i - 1] + (f[j - 1] - f[k - 1])); //B 部分
                else c = f[i - 1] + (f[k - 1] - f[j - 1]); //C 部分
                m = max(m, c);
            }
            ans = min(ans, m);
        }

    printf("%lld\n", ans);
    return 0;
}

做法二：

有如下定理：虫洞的左入口一定放在母巢。

推理证明：参考上面的图，易知借助虫洞只对 $i<k$ 的点 $k$ 有意义。对于 B 部分 $i<k<j$ 的点 $k$ 来说，最短路值只跟右入口 $j$ 位置有关，因此左入口没有限制。而对于 $j<k$ 的点 $k$ 来说，肯定是左入口在 $i=1$ 最优，至少不会变得更差。

因此可以省掉枚举左入口的一维，直接考虑右端点 $i$。

时间复杂度：$O(N^2)$
期望得分：80%
代码和上面其实差不多，就不贴了。

做法三：

直觉告诉我们，读入都要 $O(N)$，意味着不可能比它更低，但是之前内层的一维则应该可以优化，最起码要总的 $O(Nlog_2N)$ 才能过。

与 log 有关的，很容易就会想到二分。但从哪里入手呢？怎么会有单调性？

先说一个很显然的，对于 A 部分，使最短路最大的 $k$ 肯定是 $k=i$，对于 C 部分，最大值肯定是 $k=N$。也就是说，要在 B 区间内二分。

回归一下前面的式子，确定虫洞左入口为母巢之后，有

$$s(j)=min\{f_j,f_i-f_j\}\text{ if }j<i$$

不妨设 $y_1=f_j$, $y_2=f_i-f_j$，可以发现函数图象大致是这样的：

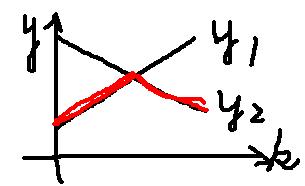
图3 函数图像示意图

由于取 min，所以只有红色部分对我们是有用的，可以发现 $min(y_1,y_2)$ 大致呈一个凸性函数。因为要求最短路的最大值，所以只要求出那个极值就可以了。

我们知道，函数交点应该满足 $y_1=y_2$。但由于本题中都是整点，一般只能尽量接近。将 $f_j=f_i-f_j$ 移项可以得到 $2\times f_j=f_i$，由于 $f_j$ 是单调递增的，根据这个条件二分即可。

求得这个点之后，由于并不是完全相等而是会有偏差，因此有必要分类讨论一下原始方法和和折返两种情况，取当中的更大值。

这里在二分时要非常小心，我改了几次都错了。区间的设置要么是左闭右开，要么是左开右闭，大于、小于和等于的情况要考虑清楚。设初值、转移和返回答案的时候，区间端点的性质都应该是统一的。

时间复杂度：$O(Nlog_2N)$
期望得分：100%
参考代码：

#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <iostream>

using namespace std;

const int MAXN = 1e5 + 100;

int N;
long long len[MAXN], f[MAXN];

long long solve(int k) { //二分找出：对于右入口放在k时，两种方法的分界点
    int l = 2, r = k; //[l, r) 左闭右开
    while (l + 1 < r) {
        int mid = l + r >> 1;
        if ((f[k] - f[mid]) <= f[mid]) r = mid; else l = mid;
    }
    return l + 1 == k ? f[l] : max(f[l], f[k] - f[r]); //注意不用走回头路的边界情况
}

int main(void) {
    freopen("2073.in", "r", stdin);
    freopen("2073.out", "w", stdout);
    scanf("%d", &N);
    for (int i = 1; i < N; i++) scanf("%lld", &len[i]);

    f[1] = 0LL; //前缀和
    for (int i = 2; i <= N; i++) f[i] = f[i - 1] + len[i - 1];

    long long ans = f[N];
    for (int i = 2; i <= N; i++) ans = min(ans, max(f[N] - f[i], solve(i))); //还要考虑 C 部分的情况
    printf("%lld\n", ans);
    return 0;
}

做到这里已经非常不错了，但是，还可以进一步优化！

做法四：

如果手动模拟（或者思维比较好）可以发现，循环时随着右入口的向右，求得的极点也会是向右的。于是就没有必要再二分了，而是可以在原先点的基础上向右移，直到得到一个合适的点即可。这就是典型的 two-pointer 做法。

时间复杂度：$O(N)$
期望得分：100%

这题实际上不是特别难，但是考得比较灵活。要求我们要能够对常用的算法熟练掌握，在手动模拟分析的过程中发现一些规律，来帮助我们推导、解题。