从零开始实现线性判别分析(LDA)算法(二类情形)

线性判别分析

声明：版权所有，转载请联系作者并注明出处:
http://blog.csdn.net/u013719780?viewmode=contents

知乎专栏：
https://www.zhihu.com/people/feng-xue-ye-gui-zi/columns

线性判别分析（Linear Discriminant Analysis或者Fisher’s Linear Discriminant）简称LDA，是一种监督学习算法。

LDA的原理是，将数据通过线性变换(投影)的方法，映射到维度更低纬度的空间中，使得投影后的点满足同类型标签的样本在映射后的空间比较近，不同类型标签的样本在映射后的空间比较远。

一、线性判别分析(二类情形)

在讲解算法理论之前，先补充一下协方差矩阵的定义。

1. 协方差矩阵定义

矩阵$X_{mxn}$协方差的计算公式：

设$x, y$分别是两个列向量，则$x, y$的协方差为

$$cov(x, y) = E(x-\bar{x})(y-\bar{y})$$

若将$x, y$合并成一个矩阵$X_{mxn}$，则求矩阵$X_{mxn}$，则矩阵$X_{mxn}$的协方差矩阵为

$$A = \sum_{i=1...m,j=1...n}a_{ij} = cov(X_i, X_j) = E(X_i-\bar{X_i})(X_j-\bar{X_j})$$

2. 算法原理

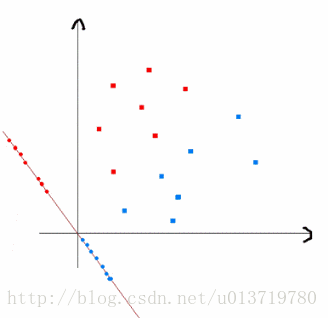
上图中红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和蓝色的点被原点明显的分开了。下面具体看看二分类LDA问题的情形：

现在我们觉得原始特征数太多，想将$n$维特征降到只有一维(LDA映射到的低维空间维度小于等于$n_{labels}-1$)，而又要保证类别能够“清晰”地反映在低维数据上，也就是这一维就能决定每个样例的类别。

假设用来区分二分类的直线（投影函数)为:

$$y=w^Tx$$

注意这里得到的$y$值不是0/1值，而是$x$投影到直线上的点到原点的距离。

已知数据集

$$D=\{x^{(1)}, x^{(1)}, …, x^{(m)}\},$$

将$D$按照类别标签划分为两类$D_1, D_2$, 其中$D_1\bigcup D_2=D, D_1\bigcap D_2=\emptyset$,
定义两个子集的中心：

$$\mu_1 = \frac{1}{n_1} \sum_{x^{(i)} \in D_1} {x^{(i)}},$$
$$\mu_2 = \frac{1}{n_2} \sum_{x^{(i)} \in D_2} {x^{(i)}},$$

则两个子集投影后的中心为

$$\tilde{\mu_1} = \frac{1}{n_1} \sum_{y^{(i)} \in \tilde{D_1}} w^T {x^{(i)}},$$
$$\tilde{\mu_2} = \frac{1}{n_2} \sum_{x^{(i)} \in D_2} w^T {x^{(i)}},$$

则两个子集投影后的方差分别为

$$\tilde{ \sigma}^2_1 = \frac{1}{n_1} \sum_{y^{(i)} \in \tilde{D_1}} ({y^{(i)}-\tilde{\mu_1}})^2 = \frac{1}{n_1} \sum_{x^{(i)} \in {D_1}} ({w^T x^{(i)}-w^T \mu_1})^2 = \frac{1}{n_1} \sum_{x^{(i)} \in {D_1}} w^T ({x^{(i)}- \mu_1}) ({x^{(i)}- \mu_1})^T w ,$$

同理可得

$$\tilde{ \sigma}^2_2 = \frac{1}{n_2} \sum_{y^{(i)} \in \tilde{D_2}} ({y^{(i)}-\tilde{\mu_2}})^2 = \frac{1}{n_2} \sum_{x^{(i)} \in {D_2}} w^T ({x^{(i)}- \mu_2}) ({x^{(i)}- \mu_2})^T w ,$$

令

$$S_1 = \frac{1}{n_1} \sum_{x^{(i)} \in {D_1}} ({x^{(i)}- \mu_1}) ({x^{(i)}- \mu_1})^T,$$

$$S_2 = \frac{1}{n_2} \sum_{x^{(i)} \in {D_2}} ({x^{(i)}- \mu_2}) ({x^{(i)}- \mu_2})^T,$$

则有

$$\tilde{ \sigma}^2_1 = w^T S_1 w, \, \tilde{\sigma}^2_2 = w^T S_2 w.$$

令

$$\tilde{S_1} = \frac{1}{n_1} \sum_{y^{(i)} \in \tilde{D_1}} ({y^{(i)}- \tilde{\mu_1}}) ({y^{(i)}- \tilde{\mu_1}})^T,$$

$$\tilde{S_2} = \frac{1}{n_2} \sum_{y^{(i)} \in \tilde{D_2}} ({y^{(i)}- \tilde{\mu_2}}) ({y^{(i)}- \tilde{\mu_2}})^T,$$

则有

$$\tilde{S_1} = w^T S_1 w, \,\,\, \tilde{S_2} = w^T S_2 w,$$

现在我们就可以定义损失函数：

$$J(w) = \frac{|\tilde{\mu}_1 - \tilde{\mu}_2|^2 }{\tilde{S}^2_1 + \tilde{S}^2_2 }$$

我们分类的目标是，使得类别内的点距离越近(集中)，类别间的点越远越好。分母表示数据被映射到低维空间之后每一个类别内的方差之和，方差越大表示在低维空间(映射后的空间)一个类别内的点越分散，欲使类别内的点距离越近(集中)，分母应该越小越好。分子为在映射后的空间两个类别各自的中心点的距离的平方，欲使类别间的点越远，分子越大越好。故我们最大化$J(w)$，求出的w就是最优的了。

因为

$$|\tilde{\mu}_1 - \tilde{\mu}_2|^2 = w^T (\mu_1 - \mu_2) (\mu_1 - \mu_2)^T w = w^T S_B w,$$

其中，

$$S_B = (\mu_1 - \mu_2) (\mu_1 - \mu_2)^T .$$

设$S_w = S_1 + S_2,$ 则

$$J(w) = \frac{w^T S_B w}{w^T S_w w}$$

这样就可以用最喜欢的拉格朗日乘数法了，但是有一个问题，如果分子、分母是都可以取任意值，就会导致有无穷解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧，在下面将说的PCA里面也会用到，如果忘记了，请复习一下高数），并作为拉格朗日乘子法的限制条件，带入得到：

$$loss(w) = w^T S_B w - (\lambda w^T S_w w -1)$$

令

$$\frac{dloss}{dw}=2 S_B w - 2 \lambda S_w w = 0,$$

则有

$$S_B w = \lambda S_w w.$$

很显然，$S_B w$和$\mu_1 - \mu_2$是平行的，又因为对$w$扩大缩小任何倍(平移$w$)不影响结果，因此，只要找到的$w$满足条件$S_B w$与$\mu_1 - \mu_2$平行即可。如果$S_w$是非奇异的，则有

$$w = S_w^{-1}{(\mu_1 - \mu_2)}.$$

下面看看具体的数学推导，

$$S_B w = (\mu_1 - \mu_2) (\mu_1 - \mu_2)^T w = (\mu_1 - \mu_2) \lambda_w .$$

将上式代入特征值公式中可得

$$S_w^{-1} S_B w = S_w^{-1} (\mu_1 - \mu_2) \lambda_w = \lambda w ,$$

因为$w$的平移不影响结果，故可以扔掉$\lambda_w , \lambda$，因此可得

$$w = S_w^{-1}{(\mu_1 - \mu_2)}.$$

得到$w$之后，就可以对测试数据进行分类了。就以二值分类为例，我们可以将测试数据投影到低维空间(直线，因为二分类问题是投影到一维空间)，得到$y$，然后看看$y$是否在超过某个阈值$y_0$，超过是某一类，否则是另一类。但是又该怎么去寻找这个$y_0$呢？

因为

$$y = w^T x,$$

根据中心极限定理，独立同分布的随机变量和服从高斯分布，然后利用极大似然估计求

$$p(y|label_i),$$

然后用决策理论里的公式来寻找最佳的$y_0$，详情请参阅PRML。这是一种可行但比较繁琐的选取方法。

其实，还有另外一种非常巧妙的方法可以确定$y_0=0$，投影之前的数据集的标签$y_{label}$是用0和1来表示，这里我们将其做一个简单的变换，

$$\begin{cases} \tilde y_{label}=\frac{m}{n_1} & \text{ if } x\in D_1 \\ \tilde y_{label}=-\frac{m}{n_2} & \text{ if } x\in D_2 \end{cases}$$

从变换后的$\tilde y_{label}$的定义可以看出，对于样本$x^{(i)}$， 若$\tilde y_{label}^{(i)}>0$，则$x^{(i)} \in D_1$，即$y^{(i)}_{label}=0$，若$\tilde y_{label}^{(i)}<0$，则$x^{(i)} \in D_2$，即$y^{(i)}_{label}=1$.

算法流程

输入：数据集$D=\{x^{(1)}, x^{(1)}, …, x^{(m)}\}$；

输出：投影后的样本集$D′$；

• 计算类内散度矩阵$S_w$；

• 求解向量$w$，其中$w = S_w^{-1}(\mu_1 - \mu_2)$；

• 将原始样本集投影到以$w$为基向量生成的低维空间中(1维)，投影后的样本集就是我们需要的样本集$D′$(1维特征)。

from sklearn import datasets
import matplotlib.pyplot as plt
%matplotlib inline
import numpy as np
import pandas as pd



def shuffle_data(X, y, seed=None):
    if seed:
        np.random.seed(seed)

    idx = np.arange(X.shape[0])
    np.random.shuffle(idx)

    return X[idx], y[idx]



# 正规化数据集 X
def normalize(X, axis=-1, p=2):
    lp_norm = np.atleast_1d(np.linalg.norm(X, p, axis))
    lp_norm[lp_norm == 0] = 1
    return X / np.expand_dims(lp_norm, axis)


# 标准化数据集 X
def standardize(X):
    X_std = np.zeros(X.shape)
    mean = X.mean(axis=0)
    std = X.std(axis=0)

    # 做除法运算时请永远记住分母不能等于0的情形
    # X_std = (X - X.mean(axis=0)) / X.std(axis=0) 
    for col in range(np.shape(X)[1]):
        if std[col]:
            X_std[:, col] = (X_std[:, col] - mean[col]) / std[col]

    return X_std


# 划分数据集为训练集和测试集
def train_test_split(X, y, test_size=0.2, shuffle=True, seed=None):
    if shuffle:
        X, y = shuffle_data(X, y, seed)

    n_train_samples = int(X.shape[0] * (1-test_size))
    x_train, x_test = X[:n_train_samples], X[n_train_samples:]
    y_train, y_test = y[:n_train_samples], y[n_train_samples:]

    return x_train, x_test, y_train, y_test


def accuracy(y, y_pred):
    y = y.reshape(y.shape[0], -1)
    y_pred = y_pred.reshape(y_pred.shape[0], -1)
    return np.sum(y == y_pred)/len(y)


# 计算矩阵X的协方差矩阵
def calculate_covariance_matrix(X, Y=np.empty((0,0))):
    if not Y.any():
        Y = X
    n_samples = np.shape(X)[0]
    covariance_matrix = (1 / (n_samples-1)) * (X - X.mean(axis=0)).T.dot(Y - Y.mean(axis=0))

    return np.array(covariance_matrix, dtype=float)



class BiClassLDA():
    """
    线性判别分析分类算法(Linear Discriminant Analysis classifier). 既可以用来分类也可以用来降维.
    此处实现二类情形(二类情形分类)
    """
    def __init__(self):
        self.w = None


    def transform(self, X, y):
        self.fit(X, y)
        # Project data onto vector
        X_transform = X.dot(self.w)
        return X_transform


    def fit(self, X, y):
        # Separate data by class
        X = X.reshape(X.shape[0], -1)

        X1 = X[y == 0]
        X2 = X[y == 1]
        y = y.reshape(y.shape[0], -1)

        # 计算两个子集的协方差矩阵
        S1 = calculate_covariance_matrix(X1)
        S2 = calculate_covariance_matrix(X2)
        Sw = S1 + S2

        # 计算两个子集的均值
        mu1 = X1.mean(axis=0)
        mu2 = X2.mean(axis=0)
        mean_diff = np.atleast_1d(mu1 - mu2)
        mean_diff = mean_diff.reshape(X.shape[1], -1)

        # 计算w. 其中w = Sw^(-1)(mu1 - mu2), 这里我求解的是Sw的伪逆, 因为Sw可能是奇异的
        self.w = np.linalg.pinv(Sw).dot(mean_diff)


    def predict(self, X):
        y_pred = []
        for sample in X:
            sample = sample.reshape(1, sample.shape[0])
            h = sample.dot(self.w)
            y = 1 * (h[0][0] < 0)
            y_pred.append(y)
        return y_pred


def main():
    # 加载数据
    data = datasets.load_iris()
    X = data.data
    y = data.target

    # 只取label=0和1的数据，因为是二分类问题
    X = X[y != 2]
    y = y[y != 2]

    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.33)

    # 训练模型
    lda = BiClassLDA()
    lda.fit(X_train, y_train)
    lda.transform(X_train, y_train)

    # 在测试集上预测
    y_pred = lda.predict(X_test)
    y_pred = np.array(y_pred)
    accu = accuracy(y_test, y_pred)
    print ("Accuracy:", accu)


if __name__ == "__main__":
    main()