机器学习从0到1——二、数学基础

本节介绍一些在后面算法的推导过程中会经常使用的数学知识。

2.1微积分与线性代数

2.1.1导数

导数定义为函数的自变量变化趋向于0时，函数值的变化量与自变量的变化值比值的极限，即

如果该极限存在，则称函数在该点处可导。导数的几何意义是函数在某一点处的切线的斜率，典型的物理意义是瞬时变化率。

下面给出基本的求导公式和法则。

下面举一个例子说明导数的计算方法，对于如下函数：

导数为：

导数和函数的单调性密切相关，导数大于0时函数单调递增，导数小于0时函数单调递减，函数在极值点处的导数必定为0。导数等于0的点称为函数的驻点。

极值：若函数f(x)在的一个邻域D有定义，且对D中除的所有点，都有f(x)<f()，则称f()是函数f(x)的一个极大值。同理，若对D中除的所有点，都有f(x)>f()，则称f()是函数f(x)的一个极小值。

如果对导数继续求导，可以得到高阶导数。将二阶导数记为：

高阶导数记为：

二阶导数决定函数的凹凸性。如果二阶导数大于0，则函数为凸函数；如果二阶导数小于0，则函数为凹函数。二阶导数等于0且在两侧异号的点称为函数的拐点。

拐点：又称反曲点，指改变曲线向上或向下方向的点，即连续曲线的凹弧与凸弧的分界点。

根据一阶导数和二阶导数，可以得到一元函数的极值判别法：在驻点处，如果二阶导数大于0，则为函数的极小值点；如果二阶导数小于0，则为极大值点；如果二阶导数等于0，则情况不定。

2.1.2向量与矩阵

向量是由多个数构成的一维数组，每个数称为它的分量。分量的数量称为向量的维数。n维向量x有n个分量，记为：

如果写成列的形式，则称为列向量：

转置运算将列向量变成行向量，将行向量变成列向量，向量x的转置记为。下面是对一个行向量的转置：

所有n维实向量构成的集合简写为。在数学上经常把向量表示成列向量；在计算机中向量一般按行存储。分量全为0的向量称为0向量。

两个向量的加法定义为向量对应元素相加，它要求参与运算的两个向量尺寸相等，如下例：

与向量加法类似，两个向量的减法为它们对应元素相减。向量与标量的乘积定义为标量与向量每个分量相乘，如下例：

两个向量x和y的内积定义为它们对应元素乘积的和，即：

如下例：

如果两个向量的内积为0，则称它们正交，它是几何中垂直这个概念在高维空间中的推广。

向量的L-P范数是一个标量，定义为：

最常用的是L1范数和L2范数。向量的L1范数为所有分量的绝对值之和，即：

向量的L2范数也称向量的模，即向量的长度，即：

如不特殊说明，后面内容的向量范数默认是L2范数。范数的定义满足三角不等式：

对于一组向量，如果存在一组不全为0的数，使

则称这组向量线性相关。如果不存在一组不全为0的数使上式成立，则称这组向量线性无关。

矩阵是一个二维数组，一个m×n的矩阵有m个行和n个列，它的每一个元素为一个数，记为：

如下例是一个2×3的矩阵：

如果矩阵的行数和列数相等，则称为方阵，n×n的方阵称为n阶方阵。如果一个方阵的元素满足：

则称该矩阵为对称阵。如下例：

如果一个矩阵除对角线上的元素之外的所有元素都为0，则称为对角矩阵。如下例：

如果一个对角矩阵的对角线上的元素全部为1，则称为单位矩阵，记为I：

矩阵的转置定义为矩阵的行和列下标相交换，一个m×n的矩阵转置之后为n×m的矩阵。矩阵A的转置记为，如下例：

对于矩阵的转置有下面这些公式成立：

两个矩阵的加法是其对应位置元素相加，显然加法运算要求两个矩阵必须有相同的尺寸。如下例：

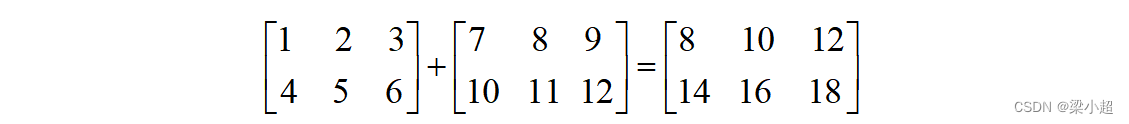
两个矩阵的减法为对应元素相减，同样，执行减法运算的两个矩阵必须尺寸相等。标量与矩阵的乘法定义为标量与矩阵的每个元素相乘，如下例：

两个矩阵的乘法定义为用第一个矩阵的每个行向量和第二个矩阵的每个列向量做内积，结果作为矩阵的每个元素，显然第一个矩阵的列数要与第二个矩阵的行数相等。如下例：

矩阵的乘法满足结合律：

(AB)C=A(BC)

以及左右分配律：

A(B+C)=AB+AC

(A+B)C=AC+BC

需要注意的是，矩阵的乘法不满足交换律，即一般情况下AB与BA不相等。

对于n阶矩阵A，如果存在另一个n阶矩阵B，使得它们的乘积为单位矩阵，即：

AB=I

BA=I

则分别称B为A的右逆矩阵和左逆矩阵，矩阵的左逆矩阵等于右逆矩阵，统称为矩阵的逆，记为。对于矩阵的逆有下面这些公式成立：

矩阵可逆的充分必要条件是其行列式不为0，或者满秩。

张量是矩阵在更高维空间的推广，可以简单地看作是编程语言里的多维数组，张量的维数称为它的阶数。一个3阶张量有3个维度的下标。标量是0阶张量，向量是1阶张量，矩阵是2阶张量。

2.1.3行列式

行列式是一个数，它是对方阵的一种映射，矩阵A的行列式记为|A|。行列式的计算公式为：

其中，表示对列标的所有排列求和，t表示排列的逆序数。

逆序数指在一个特定的排列中，如果一对数的顺序与标准顺序相反（即前一个数大于后一个数），这样的数对就被称为一个逆序。例如有一个排列[1 2 3]，序列[1 3 2]的逆序数为1，序列[3 1 2]的逆序数为2，序列[3 2 1]的逆序数为3。

如果矩阵A和B是尺寸相同的n阶矩阵，则有：

|AB|=|A||B|

即矩阵乘积的行列式等于矩阵行列式的乘积。如果矩阵可逆，其逆矩阵的行列式等于行列式的逆，即：

矩阵与标量乘法的行列式为：

其中，n为矩阵的阶数。

2.1.4偏导数与梯度

多元函数的偏导数是一元函数导数的推广。假设有多元函数，它对自变量的偏导数定义为：

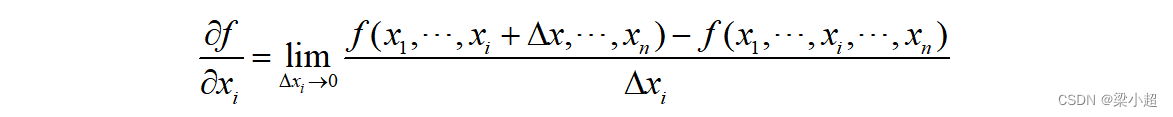
计算时，对要求导的变量进行求导，把其他变量当作常量即可，如下例：

梯度是导数对多元函数的推广，它是多元函数对每一个自变量偏导数形成的向量。梯度定义为：

其中，▽称为梯度算子，它作用于一个多元函数得到一个向量。如下例：

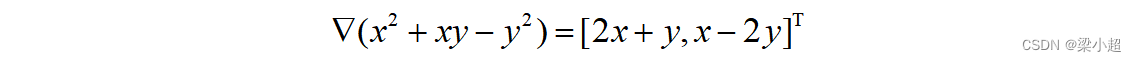
梯度与函数的单调性、极值有关。根据Fermat引理，可导函数在某一点处取得极值的必要条件是梯度为0。梯度为0的点称为函数的驻点。需要注意的是，梯度为0只是函数取得极值的必要条件而不是充分条件。

类似地，可以定义函数的高阶偏导数，这比一元函数的高阶导数复杂，因为有多个变量，以二阶偏导数为例：

表示先对x求偏导，然后再对y求偏导。如下例：

一般情况下（混合二阶偏导数连续的情况下），混合二阶偏导数与求导次序无关，即：

2.1.5雅可比矩阵

对于如下向量到向量的映射函数：

y=f(x)

其中，向量，向量，这个映射可以写成分量的形式：

即输出向量的每个分量都是输入向量的函数。雅可比矩阵是输出向量的每个分量对输入向量的每个分量的偏导数构成的矩阵：

这是一个m行n列的矩阵，每一行为一个多元函数的梯度。对于如下向量映射函数：

它的雅可比矩阵为：

雅可比矩阵可以简化多元复合函数求导的公式，后面学习反向传播算法推导过程中会有它的运用。

2.1.6 Hessian矩阵

Hessian矩阵是由多元函数的二阶偏导数组成的矩阵。如果函数二阶可导，Hessian矩阵定义为：

这是一个n阶矩阵。一般情况下多元函数的混合二阶偏导数与求导次序无关，即：

因此，Hessian矩阵是一个对称矩阵，它可以看作二阶导数对多元函数的推广。Hessian矩阵简写为。如下例：

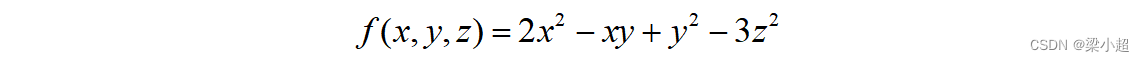
它的Hessian矩阵为：

根据多元函数极值判别法，假设多元函数在点M的梯度为0，则M是函数的驻点，有以下结论：

（1）如果Hessian矩阵正定，函数在该点处有极小值。

（2）如果Hessian矩阵负定，函数在该点处有极大值。

（3）如果Hessian矩阵不定，则不是极值点。

这是一元函数极值判别法对多元函数的推广，Hessian矩阵正定类似于一元函数二阶导数大于0。一个n阶矩阵A，如果对于任意非0的n维向量x都有：

则称矩阵A为正定矩阵。判定矩阵正定的常用方法有以下几种。

（1）矩阵的特征值全大于0.

（2）矩阵的所有顺序主子式都大于0.

（3）矩阵合同于单位阵I。

类似地，一个n阶矩阵A，如果对于任意非0的n维向量x都有：

则称矩阵A为负定矩阵。如果满足：

则称矩阵A为半正定矩阵。Hessian矩阵的正定性与多元函数的凹凸性有关，如果Hessian矩阵半正定，则函数是凸函数；如果Hessian矩阵正定，则函数是严格凸函数。

2.1.7 泰勒展开

如果一元函数n阶可导，它的泰勒展开公式为：

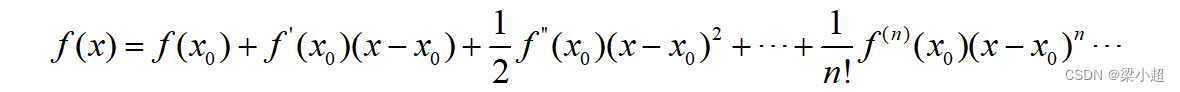
类似地，多元函数的泰勒展开公式为：

在这里o表示高阶无穷小。H是Hessian矩阵，它与一元函数的泰勒展开在形式上是统一的。

泰勒展开的意义在于它能够将一个复杂函数在某一点附近用多项式函数进行逼近。这种逼近的好处在于多项式函数具有一些便于处理的性质，例如求导数和求极值都相对简单。

2.1.8 特征值与特征向量

对于一个n阶矩阵A，如果存在一个数和一个非0向量x，满足：

则称为矩阵A的特征值，x为该特征值对应的特征向量。根据上面的定义有下面的方程组成立：

写成n元齐次线性方程组的形式：

根据线性方程组的理论，要让其次方程组有非0解，系数矩阵的行列式必须为0，即：

求解这个n次方程就可以得到所有特征值。求解矩阵特征值的经典方法是QR算法和雅可比法，这里我们不对求解方法进行讲解，因为在用python代码实现时可以利用numpy库进行求解。

矩阵的迹定义为主对角线元素之和：

矩阵所有特征值的和等于矩阵的迹：

矩阵所有特征值的积等于矩阵的行列式：

特征值和特征向量在机器学习很多算法中都有应用，典型的包括正态贝叶斯分类器、主成分分析、流形学习、线性判别分析、谱聚类等。

2.1.9 二次型

二次型是纯二次项构成的函数，写成矩阵形式为：

其中，A是n阶对称矩阵，x是一个列向量。二次型展开之后是一个二次齐次多项式，即只有二次项：

如果对于任意的非0向量x，二次型的值都大于0，则称二次型正定；如果二次型的值大于或等于0，则称二次型半正定。二次型正定等价于矩阵A正定。

2.1.10 向量与矩阵求导

为了简化表达，有时候会将函数写成矩阵和向量运算的形式，下面对常用的矩阵和向量函数的求导公式进行推导。如下向量内积函数：

x是自变量。将上式展开写成求和的形式：

函数对每个自变量的偏导数为：

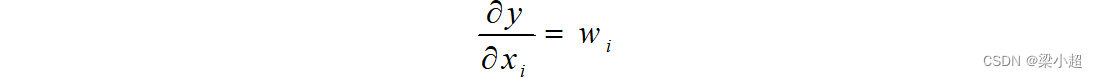
从而得到梯度的计算公式为：

对于如下二次函数：

x是自变量。上式展开后的形式为：

根据上面的展开可以得到对每个自变量的偏导数为：

从而得到梯度的计算公式为：

如果A是对称矩阵，上式可化简为：

进一步我们可以得到二阶偏导数为：

上式成立是因为只有这两个求和项含有，其他求和项的偏导数都为0。写成矩阵形式，可以得到Hessian矩阵为：

如果A是对称矩阵，上式可以简化为：

参考文献

雷明. 机器学习——原理、算法与应用．清华大学出版社.