机器学习从0到1——2.2概率论基础

最新推荐文章于 2024-07-11 15:21:16 发布

梁小超

最新推荐文章于 2024-07-11 15:21:16 发布

阅读量766

点赞数 16

分类专栏：机器学习从0到1 文章标签：机器学习概率论人工智能

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/u013867253/article/details/138560653

版权

机器学习从0到1 专栏收录该内容

11 篇文章 0 订阅

订阅专栏

2.2概率论

如果把机器学习处理的变量看成是随机变量，则可以用概率论的方法建模。本节简单介绍机器学习将要使用的概率论知识。

2.2.1随机事件与概率

随机事件a是指可能发生也可能不发生的事件，它有一个发生概率p(a)，且该概率值满足如下约束：

$0\leq p(a)\leq 1$

即概率值为0~1，这个值越大，事件越可能发生，如果一个随机事件发生的概率为0，称为不可能事件；如果一个随机事件发生的概率为1，则称为必然事件。例如：抛一枚硬币，可能正面朝上，也可能反面朝上，两种事件发生的概率是相等的，各为0.5。

2.2.2条件概率

对于两个相关的随机事件a和b，在事件a发生的条件下事件b发生的概率称为条件概率p(b|a)，定义为：

$p(b\mid a)=\frac{p(a,b)}{p(a)}$

即a和b同时发生的概率与a发生的概率的比值。如果事件a是因，事件b是果，则概率p(a)称为先验概率。后验概率定义为：

$p(a\mid b)=\frac{p(a,b)}{p(b)}$

先验概率是指根据以往经验分析得到的概率，往往作为“由因求果”问题中的“因”出现的概率。

后验概率是指事件已将发生了，有多种原因，判断事情的发生是由哪一种原因引起的，是“由果求因”。

贝叶斯公式指出：

$p(a)p(b\mid a)=p(b)p(a\mid b)$

变形后为：

$p(a\mid b)=\frac{p(a)p(b\mid a)}{p(b)}$

贝叶斯公式描述了先验概率和后验概率之间的关系。如果有p(b|a)=p(b)，或者p(a|b)=p(a)，则称随机事件a和b独立。如果随机事件a和b独立，则有：

$p(a,b)=p(a)p(b)$

将上面的结论进行推广，如果n个随机事件 $a_{i},i=1,2,\cdots,n$ 相互独立，则它们同时发生的概率等于它们各自发生的概率的乘积：

$p(a_{1},a_{2},\cdots,a_{n})=\prod_{i=1}^{n}p(a_{i})$

2.2.3随机变量

随机变量是一个随机事件结果的可能数值。它分为离散型和连续型两种，离散型随机变量的取值为有限个或者无限可列个（例如整数集），连续性随机变量的取值为无限不可列个（例如实数集）。

描述离散型随机变量分布情况的是概率质量函数，它由随机变量取每个值的概率 $p(x=x_{i})=p_{i}$ 依次排列组成。它满足：

$p_{i}\geq 0$

$\sum p_{i}=1$

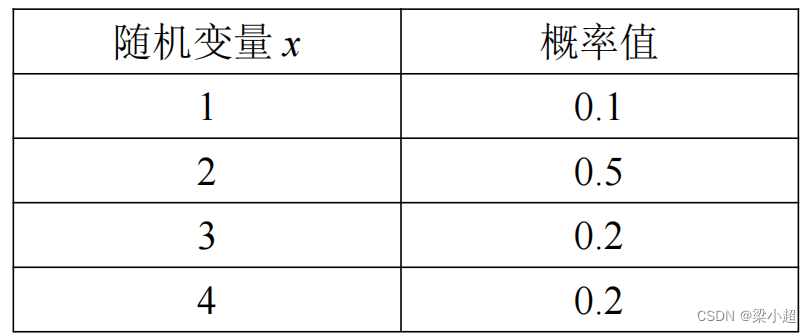
下表是一个随机变量概率质量函数的例子：

把概率质量函数推广到无限的情况，就可以得到连续型随机变量的概率密度函数。一个函数如果满足如下条件，则可以称为概率密度函数：

$f(x)\geq 0$

$\int_{-\infty}^{+\infty}f(x)dx=1$

这可以看作离散型随机变量的推广，积分值为1对应于取各个值得概率之和为1。分布函数是随机变量 $x\leq y$ 的概率，它是概率密度函数的变上限积分，定义为：

$F(y)=p(x\leq y)=\int_{-\infty}^{y}f(x)dx$

$p(x_{1}<x<x_{2})=\int_{x_{1}}^{x_{2}}f(x)dx=F(x_{2})-F(x_{1})$

最常见的连续型概率分布是正态分布，也称高斯分布。它的概率密度函数为：

$f(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^{2}}{2\sigma^{2}}}$

其中， $\mu$ 和 $\sigma^{2}$ 分别为均值和方差。现实世界中的很多数据，例如人的身高、体重、寿命等都近似服从正态分布。另外一种常见的分布是均匀分布，如果随机变量x服从[a,b]的均匀分布，则其概率密度函数为：

${f(x)}= \begin{cases} \frac{1}{b-a},&a\leq x\leq b \\ {0,}&x<a ,x>b \end{cases}$

伯努利分布也是一种常见的分布，这是一种离散型随机变量的概率分布，变量取值只有0和1，取这两种值得概率为：

$p(x=0)=p$

$p(x=1)=1-p$

其中，p为[0,1]得一个实数。对于二分类问题，分类结果可以看作伯努利分布。

2.2.4数学期望与方差

数学期望是加权平均值的抽象，是随机变量在概率意义下的均值。对于离散型随机变量x，数学期望定义为：

$E(x)=\sum x_{i}p(x_{i})$

例如前面的概率质量函数的表格，它的数学期望为：

1×0.1+2×0.5+3×0.2+4×0.2=2.5

方差定义为：

$D(x)=\sum (x_{i}-E(x))^{2}p(x_{i})$

对于前面表格中的随机变量，它的方差为：

$(1-2.5)^{2}\times 0.1+ (2-2.5)^{2}\times 0.5+ (3-2.5)^{2}\times 0.2+ (4-2.5)^{2}\times 0.2=0.85$

推广到连续型随机变量的情况，假设有一个连续型随机变量x的概率密度函数是f(x)，其数学期望定义为：

$E(x)=\int_{-\infty}^{+\infty}xf(x)dx$

连续型随机变量的方差定义为：

$D(x)=\int_{-\infty}^{+\infty}(x-E(x))^{2}f(x)dx$

方差反应的是随机变量取值变化的程度，方差越小，随机变量的变化幅度越小，反之越大。

2.2.5随机向量

前面定义的随机变量是单个变量，如果推广到多个变量，就得到随机向量。随机向量x是一个向量，它的每个分量都是随机变量。同样，随机向量有离散型和连续型两种情况。描述离散型随机向量分布的是联合概率质量函数：

$p(x=x_{i})$

对于二维离散型随机向量，这是一个二维表：

$p(x=x_{i},y=y_{j})$

描述连续型随机向量的是联合概率密度函数，这是一个多元函数。如果是二维随机向量，则其联合概率密度函数满足：

$f(x_{1},x_{2})\geq=0$

$\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}f(x_{1},x_{2})dx_{1}dx_{2}=1$

更高维的概率密度函数也需要满足这两个条件。

对于离散型随机向量，边缘概率定义为：

$p(x=x_{i})=\sum_{y}p(x=x_{i},y=y_{j})$

对于连续型随机向量，边缘密度函数定义为：

$f(x_{1})=\int_{-\infty}^{+\infty}f(x_{1},x_{2})dx_{2}$

$f(x_{2})=\int_{-\infty}^{+\infty}f(x_{1},x_{2})dx_{1}$

条件概率密度函数定义为：

$f(x_{1}\mid x_{2})=\frac{f(x_{1},x_{2})}{f(x_{2})}$

有了条件概率密度函数，就可以定义两个随机变量之间的独立性：

$f(x_{1}\mid x_{2})=f(x_{1})$

显然，如果两个随机变量独立，则有：

$f(x_{1}, x_{2})=f(x_{1})f(x_{2})$

协方差描述两个随机变量总体误差的期望，它能够描述两个变量的相关程度，定义为：

$cov(x_{1},x_{2})=E((x_{1}-E(x_{1}))(x_{2}-E(x_{2})))\\ =E(x_{1}x_{2})-2E(x_{2})E(x_{1})+E(x_{1})E(x_{2})=E(x_{1}x_{2})-E(x_{1})E(x_{2})$

对于n维随机向量x，其任意两个分量 $x_{i}$ 和 $x_{j}$ 之间的协方 $cov(x_{i},x_{j})$ 差组成的矩阵称为协方差矩阵，协方差矩阵是一个对称矩阵。

将一维的正态分布推广到高维，可以得到多维正态分布概率密度函数：

$f(x)=\frac{2}{(2\pi)^{\frac{n}{2}}\mid\Sigma\mid^{\frac{1}{2}}}\text{exp}(-\frac{(x-\mu)^{T}(x-\mu)}{2\Sigma})$

其中，x为n维随机向量， $\mu$ 为均值向量， $\Sigma$ 为协方差矩阵。

2.2.6最大似然估计

有些应用中已知样本服从的分布，例如服从正态分布，但是需要估计分布函数的参数 $\theta$ ，例如均值和协方差。确定这些参数常用的一种方法是最大似然估计。

最大似然估计（Maximum Likelihood Estimate，MLE）构造一个似然函数，通过让似然函数最大化求解出 $\theta$ 。

假设样本服从的概率密度函数为 $p(x;\theta)$ ，其中，x为随机变量， $\theta$ 为要估计的参数。给定一组样本 $x_{i},i=1,2,...,l$ ，它们都服从这种分布，并且相互独立。构造如下似然函数：

$L(\theta)=\prod_{i=1}^{l}p(x_{i};\theta)$

这是一个关于 $\theta$ 的函数，要让该函数的值最大化，这样做的依据是应该最大化这组样本发生的概率。即求解如下最优化问题：

$\text{max}\prod_{i=1}^{l}p(x_{i};\theta)$

乘积求导不易处理，因此对该函数取对数，得到对数似然函数：

$\text{ln}L(\theta)=\text{ln}\prod_{i=1}^{l}p(x_{i};\theta)=\sum_{i=1}^{l}\text{ln}p(x_{i};\theta)$

最后要求解的问题变为：

$\text{max}\sum_{i=1}^{l}\text{ln}p(x_{i};\theta)$

这是一个不带约束的优化问题，可以用梯度下降法或者牛顿法直接求解析解。后面讲解算法时我们会对这两种求解方法进行讲解。

参考文献

雷明. 机器学习——原理、算法与应用．清华大学出版社.

关注

16
点赞
踩
12

收藏

觉得还不错? 一键收藏
0
评论
机器学习从0到1——2.2概率论基础

机器学习从0到1数学基础第二部分概率论相关知识
复制链接

扫一扫

专栏目录

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。