1多项式加法(5分)
题目内容:
一个多项式可以表达为x的各次幂与系数乘积的和,比如:
现在,你的程序要读入两个多项式,然后输出这两个多项式的和,也就是把对应的幂上的系数相加然后输出。
程序要处理的幂最大为100。
输入格式:
总共要输入两个多项式,每个多项式的输入格式如下:
每行输入两个数字,第一个表示幂次,第二个表示该幂次的系数,所有的系数都是整数。第一行一定是最高幂,最后一行一定是0次幂。
注意第一行和最后一行之间不一定按照幂次降低顺序排列;如果某个幂次的系数为0,就不出现在输入数据中了;0次幂的系数为0时还是会出现在输入数据中。
输出格式:
从最高幂开始依次降到0幂,如:
2x6+3x5+12x3-6x+20
注意其中的x是小写字母x,而且所有的符号之间都没有空格,如果某个幂的系数为0则不需要有那项。
输入样例:
6 2
5 3
3 12
1 6
0 20
6 2
5 3
2 12
1 6
0 20
输出样例:
4x6+6x5+12x3+12x2+12x+40
时间限制:500ms内存限制:32000kb
#include<stdio.h>
int main()
{
int cnta[101],a,n,i,j,cntb[101],k,b;
for(i=0;i<101;i++){
cnta[i]=0;
cntb[i]=0;
}
scanf("%d %d",&n,&a);//input array a[]
i=n;
while(n!=0)
{
cnta[n]=a;
scanf("%d %d",&n,&a);
}
cnta[0]=a;
//input array b[]
scanf("%d %d",&k,&b);
while(k!=0)
{
cntb[k]=b;
scanf("%d %d",&k,&b);
}
cntb[0]=b;
//sum a[] and b[]
for(j=0;j<=i;j++)
{
cnta[j]=cnta[j]+cntb[j];
}
while(i!=0)
{
if(cnta[i]!=0)
{
if(i!=1){
printf("%dx%d",cnta[i],i);
}else{
printf("%dx",cnta[i]);
}
for(j=i;j>0;)
{
if(cnta[--j]!=0)
{
printf("+");
break;
}
}
}
i--;
}
if(cnta[0]!=0)
printf("%d\n",cnta[0]);
else
printf("\n");
return 0;
}
2鞍点(5分)
题目内容:
给定一个n*n矩阵A。矩阵A的鞍点是一个位置(i,j),在该位置上的元素是第i行上的最大数,第j列上的最小数。一个矩阵A也可能没有鞍点。
你的任务是找出A的鞍点。
输入格式:
输入的第1行是一个正整数n, (1<=n<=100),然后有n行,每一行有n个整数,同一行上两个整数之间有一个或多个空格。
输出格式:
对输入的矩阵,如果找到鞍点,就输出其下标。下标为两个数字,第一个数字是行号,第二个数字是列号,均从0开始计数。
如果找不到,就输出
NO
题目所给的数据保证了不会出现多个鞍点。
输入样例:
4
1 7 4 1
4 8 3 6
1 6 1 2
0 7 8 9
输出样例:
2 1
时间限制:500ms内存限制:32000kb
#include <stdio.h>
int main()
{
int n, flag = 0,i,j,min=0,max=0;
scanf("%d", &n);
int arr[n][n];
for(i=0; i<n; ++i)
{
for(j=0; j<n; ++j)
{
scanf("%d", &arr[i][j]);
// printf("arr[%d][%d]=%d\n",i,j,arr[i][j]);
}
}
for(i=0; i<n; ++i)
{
for(j=1; j<n; ++j)
{
if(arr[i][j]>arr[i][max])
{
max = j;
}
}
for(j=1; j<n; ++j)
{
if(arr[j][max]<arr[min][max])
{
min = j;
}
}
if(i == min)
{
flag = 1;
printf("%d %d\n", min, max);
break;
}
}
if(!flag)
printf("NO\n");
return 0;
}








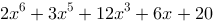














 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








