python 用蒙特卡罗方法计算圆周率

最新推荐文章于 2025-03-22 08:26:44 发布

二仪式

最新推荐文章于 2025-03-22 08:26:44 发布

阅读量1.8w

点赞数 8

分类专栏： python 文章标签： python pi random 蒙特卡洛计算思想

本文链接：https://blog.csdn.net/u013894427/article/details/80329355

版权

python 专栏收录该内容

29 篇文章

订阅专栏

本文介绍了一种使用蒙特卡洛方法来估算圆周率的方法。该方法通过随机生成大量的坐标点并统计这些点落在单位圆内的比例来估算圆周率的值。随着生成点数的增加，估算的精度也随之提高。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

蒙特卡洛方法

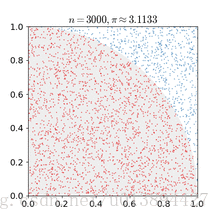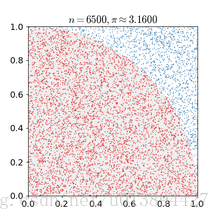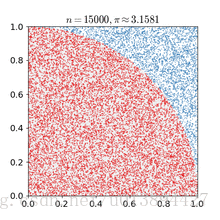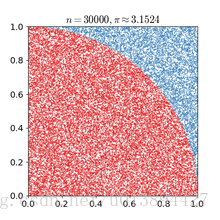
蒙特卡罗方法基于这样的思想：假想你有一袋豆子，把豆子均匀地朝这个图形上撒，然后数这个图形之中有多少颗豆子，这个豆子的数目就是图形的面积。当你的豆子越小，撒的越多的时候，结果就越精确。借助计算机程序可以生成大量均匀分布坐标点，然后统计出图形内的点数，通过它们占总点数的比例和坐标点生成范围的面积就可以求出图形面积。

蒙特卡洛方法

代码

import time
import random
hits=0
pi=0
DARTS=10000*10000
start=time.perf_counter()
for i in range(DARTS):
    x,y=random.random(),random.random()
    dist=pow(x ** 2+y**2,0.5)
    if dist <= 1.0:
        hits+=1
pi=4*(hits/DARTS)
print("圆周率的值是{:.10f}".format(pi))
print("程序运行时间为{}s".format(time.perf_counter()-start))