解决终身学习问题,即主要解决灾难性遗忘的问题,通常来讲学术界有几种主要的研究思 路。我们首先将第一种主要的解法,即选择性的突触可塑性(selectivesynapticplasticity)。顾 名思义,就是只让神经网络中的某些神经元之间的连接具有可塑性,其余的必须被固化,这类 方法又叫做基于正则的方法。我们可以先回顾一下会什么发生灾难性遗忘这种现象,例如现在 有任务一和任务二,并且处于简化考虑,假设训练的模型只有两个参数θ1和θ2。如图1所 示,分别表示了模型在不同任务上的损失函数,如果颜色越偏蓝色,代表损失越小,反之越大。
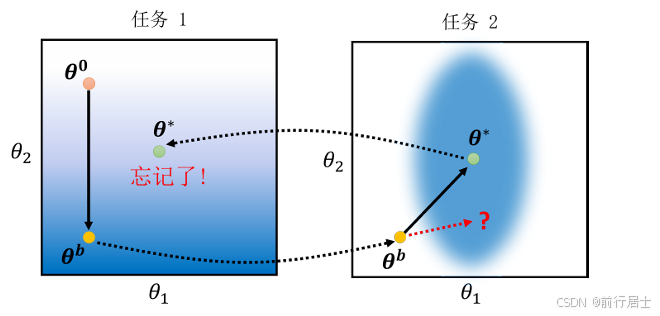
图1 灾难性遗忘示意图
我们先让模型训练任务一,比如给一个随机化的初始参数θ0,用梯度下降的方法更新足 够多次数的参数后得到θb。接下来继续训练任务二,我们先把θb复制过来放到任务二上,那 么由于任务二的损失截面是不同的,即蓝色的区域不同,通过多次迭代我们可能会把参数更 新到θ∗ 的位置。然后我们把在任务二上训练好的参数θ∗ 拿回到任务一上使用时,会发现并 没有办法得到好的结果。因为这个θ∗只是在任务二上表现较好,而不见得会在任务一上有较 低的损失和好的表现,这就是灾难性遗忘产生的原因。
那怎么解决这个问题呢?其实对于一个任务而言,要实现较低的损失是可能有很多种不 同的参数组合的,比如在任务二中可能所有椭圆内的参数都能有好的表现,而对于任务一则 是偏下方的位置都能实现较低的损失。那么如果在跑完任务一之后在训练任务二时,我们的 参数不是像右上角移动形成θ∗,而是只往右移动,让最终得到的参数同时处于任务一和任务 二较低的损失区域,这种情况下是有可能不会产生灾难性遗忘的。对于这种方式,基本的思想 就是每一个参数对我们过去学过的任务的重要性程度是不同的,因此在学习新的任务时,我们尽量不要动那些对过去任务很重要的参数,而是去学一些其他的对新任务比较重要的参数。 假设θb 是前一个任务学出来的参数,在选择性的突触可塑性这一解法中会给每一个参数θb i 赋予一个系数bi,这个系数代表着对应的参数对过去的任务到底重不重要,也称作“守卫”。因 此在更新参数的时候,会改写损失函数,如下:
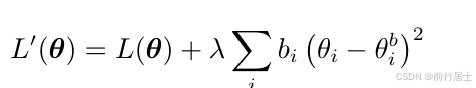
原来的损失函数写成L(θ),在学习新任务时不会直接去最小化这个损失函数,否则就会 发生灾难性遗忘的问题。我们会在右边一项增加一个当前参数θi 与之前对应的参数θb i 的平 均差并乘上我们讲的重要性系数bi。这里bi=0时,表示我们并不关心学习新任务时的参数 需要跟过去的参数有什么联系,即一般的训练,这种情况下就容易发生遗忘。另一种极端就 是当bi 趋近于无穷大时,即模型参数不肯在新任务上发生妥协,此时可能不会忘记旧的任务, 但是也很有可能学不好新的任务,这种情况我们称作不妥协。
接下来比较关键的是bi要怎么设定的问题,也就是某个参数bi到底对任务的重要性有多 少。其实有一种简单的控制变量的方法,就是移动或改变某个参数,如图2所示,我们移 动θb 1 时会发现在一定范围内损失值都是很小的,即接近最优的参数,那么我们就可以认为这 个参数在一定范围可变,相应的重要性参数b1就可以很小,即这个参数对旧任务来说不是很 重要,反之像θb 2 这种不能随意移动的参数对应的重要性参数就必须很大。
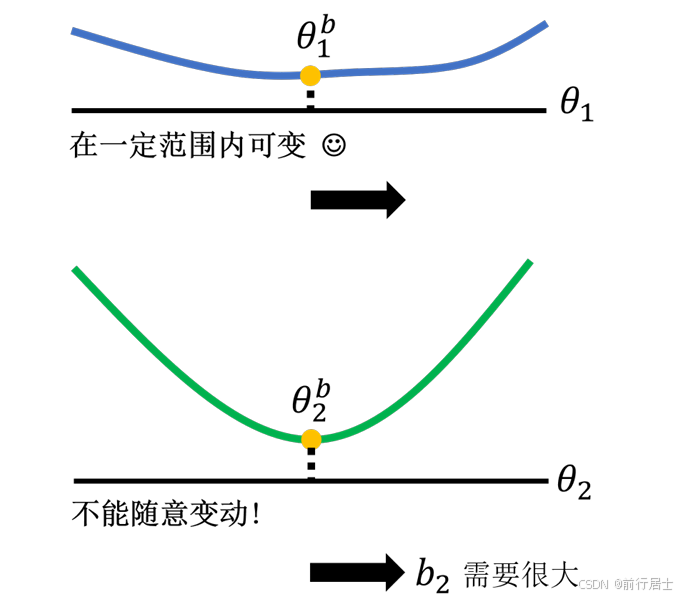
图2 重要性参数设定示例
当然随着后续研究的深入,bi 的设定也会有各种各样的方法,感兴趣的读者可以了解相 关论文,这里就不一一讲解了 .
其实在基于正则的方法出现之前,还有一类方法,叫做梯度回合记忆(gradientepisodic memory,MMD),它不是在参数上做限制,而是在梯度更新的方向上做限制,因此又被称 为基于梯度的方法。原理如图3所示,它在计算当前任务梯度方向的同时,也会回去算历 史任务对应的梯度方向,然后把两个梯度进行向量求和,得出实际的梯度方向,这样持续更新 就能尽可能接近一个不会陷入灾难性遗忘的最优解了。当然新的梯度方向需要满足大于等于0 的条件,否则很难朝最优解方向优化。
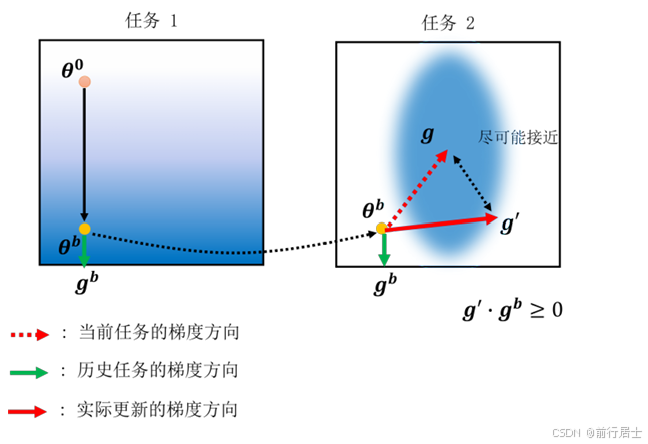
图3 GEM 方法示例
但是这类方法需要把过去的数据同时存储下来,其实这跟终身学习的初衷有些违背了,因 为终身学习本身就是希望不需要依赖过去的数据。但由于这里只是存储梯度这些少量的信息, 像前面讲的选择性的突触可塑性方法也需要存储一些历史模型信息,所以在实际操作过程中 也还能接受。





















 6410
6410

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








