问题描述:
给定有n个整数(可能为负整数)组成的序列,a1,a2,.......an,求该序列如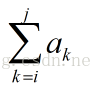
最优值为
Max{0, 
上述假定的意思也就是说最大字段和(只有一个字段)要么为0,要么大于0
int MaxSum(int n,int *a,int &besti,int &bestj)
{
//穷举法遍历数组a
int sum=0;
for(int i=1;i<=n;i+)
for(int j=i;j<=n;j++) //例如i=1时,算出1~1,1~2......1~n字段的和
{
int thissum=0;
for(int k=i;k<=j;k++)
thissum+=a[k];
if(thissum>sum) //如果字段和大于当前最大子段和sum,则更新
{
sum=thissum;
besti=i;
bestj=j;
}
} //这样下来就可以在i=1时找到其中的最大字段和的值,下标i和j
return sum;
} //重复查找,很明显时间复杂度O(n^3)
仔细分析一下,第三个循环做了重复的工作,当j++后,thissum没必要又从i...j计算一遍,只需要thissum+=a[j],便可将时间复杂度降低到O(n^2)
int MaxSum(int n,int *a,int &besti,int &bestj)
{
int sum=0;
for(int i=1;i<=n;i++)
{
int thissum=0;
for(int j=i;j<=n;j++)
{
thissum+=a[j];
if(thissum>sum)
{
sum=thissum;
besti=i;
bestj=j;
}
}
}
return sum;
}
针对最大字段和问题的解结构,它也适合分治法求解。
为什么这么说呢,因为分而治之的思想能够降低该问题规模,同时该问题适合进行递归求解。
那么如果按照n/2来划分,那么a[1....n]最大子段和有三种情况
1>a[1:n]最大子段和与a[1:n/2]的最大子段和相同
2>a[1:n]最大子段和与a[n/2+1:n]的最大子段和相同
3> a[1:n]的最大子段和为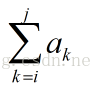
针对一,二两种情况可用递归求得,那么第三种情况可以在a[1:n/2],a[n/2+1:n]计算其最大字段和s1,s2,然后相加s1+s2即为情形3的最优值,
int MaxSubSum(int *a,int left,int right)
{
int sum=0;
if(left==right) //出口落脚在单个值是否大于0
sum=a[left]>0?a[left]:0;
else
{
int center=(left+right)/2;
int leftsum=MaxSubSum(a,left,center); //在每个子序列中获取满足条件的三种情况下的值
int rightsum=MaxSubSum(a,center+1,right);
int s1=0; //找到在情形3下的最大字段和
int lefts=0;
for(int i=center;i>=left;i--) //注意到是从center即中间往两侧寻找最大子段
{
lefts+=a[i];
if(lefts>s1)
s1=lefts;
}
int s2=0;
int rights=0;
for(int j=center+1;j<=right;j++) //注意j这里是从center+1
{
rights+=a[j];
if(rights>s2)
s2=rights;
}
sum=s1+s2; //然后取其中最大值
if(sum<leftsum)
sum=leftsum;
if(sum<rightsum)
sum=rightsum;
}
return sum;
}对于动态规划法,得好好理解其思想,即何为动态规划,我的理解是先从整体上找到规律,然后再自底向上求解,同时要注意这个底部即最小规模时问题的分析。
这里我们先假设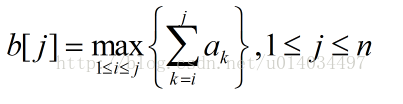
既然b[j]表示我们所求的某个当前最大字段和,那么当b[j-1]>0时,b[j]=b[j-1]+a[j],否则,b[j]=a[j](因为b[j-1]都小于0了,如果a[j]>0这样做只会拉低b[j],如果a[j]<0,摒弃b[j-1]只会对b[j]更有利,所以无论a[j]正负,只要b[j-1]<0,我就摒弃它,而只将a[j]作为b[j]的值;)
所以可得b[j]的动态规划递归式:
int MaxSum(int n,int *a)
{
int sum=0,b=0; //sum记录的是当前最大字段和,用作保存和参照的,而b是当前运行时的最大字段和,
for(int i=1;i<=n;i++)
{
if(b>0)
b+=a[i];
else
b=a[i];
if(b>sum)
sum=b;
}
return sum;
}
这是一维情形下的最大子段和,那么二维下呢,比如说二维矩阵
常规思路时间复杂度O(m^2 n^2)
式中
设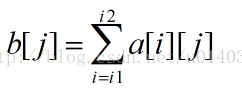
先上代码,该算法时间复杂度O(m^2 n)
int MaxSum2(int m,int n,int **a)
{
int sum=0;
int *b=new int[n+1];
for(int i=1;i<=m;i++) //m表示行
{
for(int k=1;k<=n;k++) b[k]=0;
for(int j=i;j<=m;j++)
{
for(int k=1;k<=n;k++)
{
<span style="color:#FF0000;"><strong>b[k]+=a[j][k];</strong></span>//表示b[2]=a[1][2]+....+a[m][2],所以才会形成矩阵(子矩阵),这里相当于将同列多行压缩成一列一行,便于
//MaxSum(n,b)计算所谓的最大子段和,即最大子矩阵和,就是图中的红色区域
}
int max=MaxSum(n,b);
if(max>sum)
sum=max;
}
}
return sum;
}
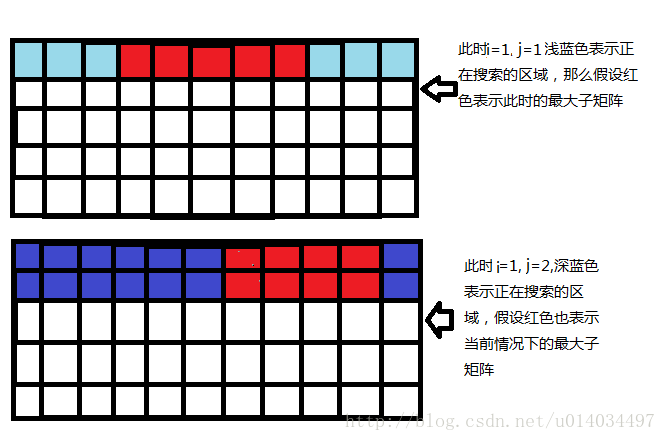
上图是表示i=1,j=1..m,k=1...n的情况,一轮k下来,可得到i,j确定时,矩阵的最大子矩阵和,一轮j下来,可得到i确定时,矩阵的最大子矩阵和
那么接下来看看,i=2时,如何得到最大子矩阵,这样的一轮下来,便可得到整个矩阵的最大子矩阵和








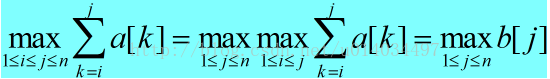

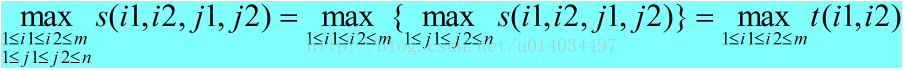
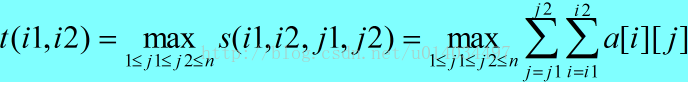
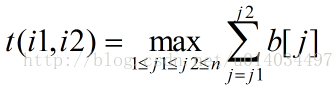















 255
255

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








