PRML 第二章 Beta分布

学习Beta分布之前，先补充一下几个相关的基础知识。
1. 共轭分布
如果后验分布和先验分布具有相同的函数形式，则先验和后验叫做共轭分布，并且先验叫做似然的共轭先验。
2. 超参数
当参数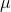为随机变量时，该参数分布中的参数就是超参数，简单的说就是参数的参数（超参数控制了参数的概率分布），在贝叶斯方法中出现的比较多。
3. Beta分布引入
现在假设我们扔一个硬币3次，碰巧3次都是正面朝上。那么N = m = 3，（m为正面向上的次数，N为实验的总次数）且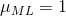(见上一篇博客)。这种情况下，最大似然的结果会预测所有未来的观测值都是正面向上，常识告诉我们这个是不合理的。
为了⽤贝叶斯的观点看待这个问题，我们需要引⼊⼀个关于µ的先验概率分布p(µ)。为了数学形式上的一致和后续计算的方便，选择一个跟似然函数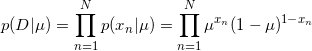（）具有函数形式一致性的先验概率，这样计算得到的后验分布（正⽐于先验和似然函数的乘积）就会具有与先验分布相同的函数形式（共轭分布）。因此，可以把先验分布选择为Beta分布。
4. Beta分布
Beta分布定义为：
，其中为Gamma函数，当n为整数时有.
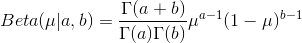
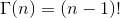
Beta分布的均值和⽅差为:
（1）

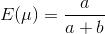
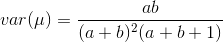
2016.6.6 补充：其实beta分布就是二项分布推广成实数域上的情况而已！
5.µ的后验概率
µ的后验概率分布现在可以这样得到：把Beta先验与⼆项分布的似然函数相乘，然后归⼀化。只保留依赖于µ的因⼦，我们看到后验概率分布的形式为：
, 其中l = N − m，即对应于硬币“反⾯朝上”的样本数量。实际上，它仅仅是另⼀个Beta分布。通过与Beta分布对⽐，我们可以得到它的归⼀化系数。因此µ的后验概率分布：
（*）
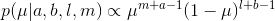
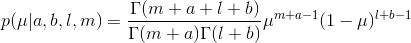
如果⼀个数据集⾥有m次观测为x = 1，有l次观测为x = 0，那么从先验概率到后验概率， a的值变⼤了m， b的值变⼤了l。这让我们可以简单地把先验概率中的超参数a和b分别看成x = 1和x = 0的有效观测数。注意， a和b不⼀定是整数。
6. 顺序学习方法
顺序⽅法每次使⽤⼀个观测值，或者每次使⽤⼀⼩批观测值，然后在使⽤下⼀个观测值之前丢掉它们。例如，顺序⽅法可以被⽤于实时学习的场景中。在实时学习的场景中，输⼊为⼀个稳定持续的数据流，模型必须在观测到所有数据之前就进⾏预测。由于顺序学习的⽅法不需要把所有的数据都存储到内存⾥，因此顺序⽅法对于⼤的数据集也很有⽤。
举例：如果我们的⽬标是尽可能好地预测下⼀次试验的输出，那么我们必须估计出给定观测数据集D的情况下， x的预测分布，即：

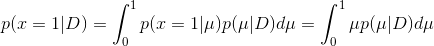
又因为：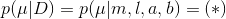
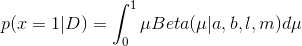
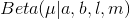
所以:， 即为的数学期望。
由公式（1）可以得到：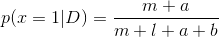
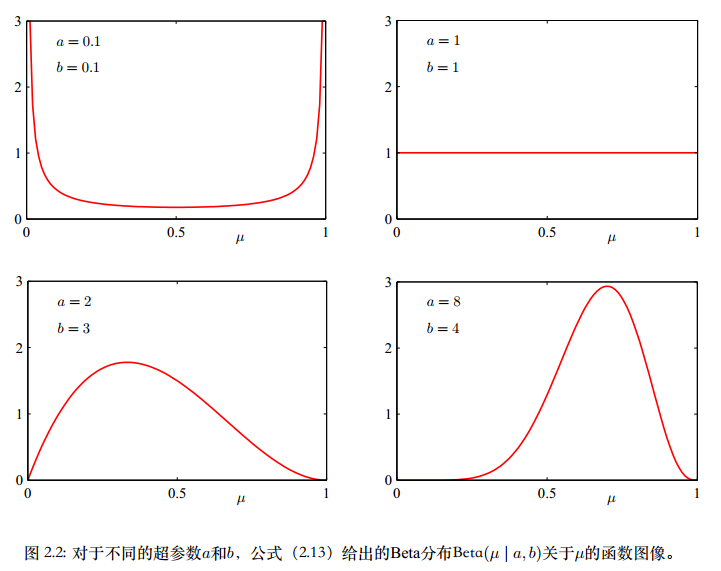
如果我们接下来观测到更多的数据，那么后验概率分布可以扮演先验概率的⾓⾊。为了说明这⼀点，我们可以假想每次只取⼀个观测值，然后在每次观测之后更新当前的后验分布。更新⽅法是观测到⼀个x = 1仅仅对应于把a的值增加1，⽽观测到x = 0会使b增加1。同时我们可以看到，当观测的数量增加时，后验分布的图像变得更尖了。如果a → ∞或者b → ∞，那么⽅差就趋于零。即随着我们观测到越来越多的数据，后验概率表⽰的不确定性将会持续下降。