搞懂间隔
给定训练样本集
D
=
{
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
m
,
y
m
)
}
,
y
i
∈
{
−
1
,
+
1
}
D={\{(x_{1},y_{1}),(x_{2},y_{2}),...,(x_{m},y_{m})\}},y_{i} \in \{-1,+1\}
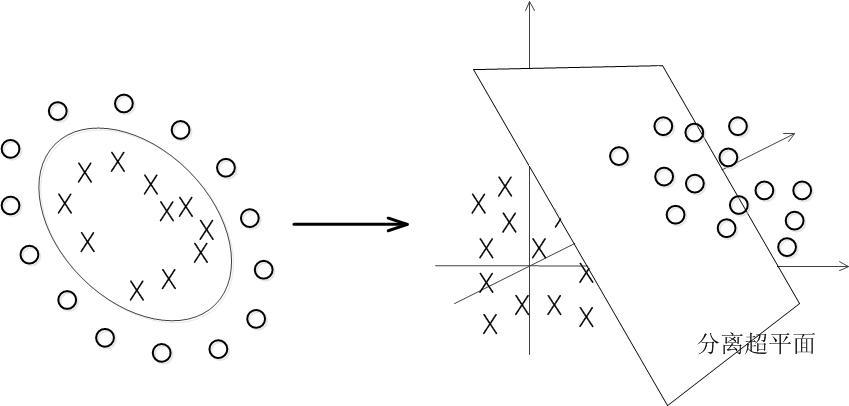
D={(x1,y1),(x2,y2),...,(xm,ym)},yi∈{−1,+1},分类学习最基本的想法就是基于训练集
D
D
D在样本空间中找到一个划分超平面,将类别分开。如下图所示。
但是能将样本分开的超平面有很多,直观上看,应该找两类训练样本“正中间”的超平面,让两类“相离”最远。
超平面可通过如下线性方程来描述:
w
T
x
+
b
=
0
,
w^Tx+b=0,
wTx+b=0,
其中
w
=
(
w
1
;
w
2
;
.
.
.
;
w
d
)
w=(w_1;w_2;...;w_d)
w=(w1;w2;...;wd)为超平面法向量,决定超平面的方向;b为位移项,决定超平面与原点之间的距离。
超平面记为
(
w
,
b
)
(w,b)
(w,b),接下来说明所谓的“间隔”。
如上图,中间的实现表示的为超平面
(
w
,
b
)
(w,b)
(w,b),假设超平面能正确分类,即对于
(
x
i
,
y
i
)
∈
D
(x_i,y_i) \in D
(xi,yi)∈D,若
y
i
=
+
1
y_i=+1
yi=+1,则有
w
T
x
+
b
>
0
w^Tx+b>0
wTx+b>0;若
y
i
=
−
1
y_i=-1
yi=−1,则有
w
T
x
+
b
<
0
w^Tx+b<0
wTx+b<0。令
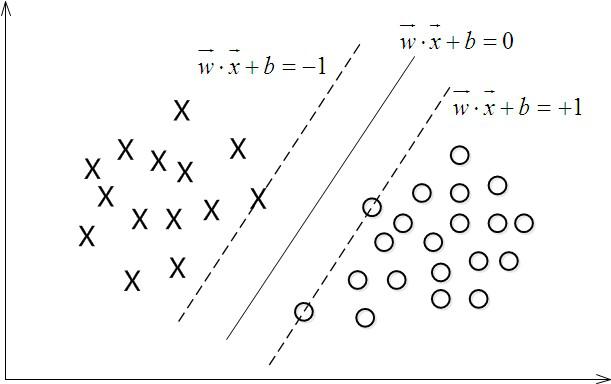
{ w T x + b ≥ + 1 , y i = + 1 w T x + b ≤ − 1 , y i = − 1 \left\{\begin{matrix} w^Tx+b \geq +1,&y_i=+1 \\ w^Tx+b\leq-1,& y_i=-1 \end{matrix}\right. {wTx+b≥+1,wTx+b≤−1,yi=+1yi=−1
在上图中,距离超平面最近的这几个样本点使得上式的等号成立,它们就被称为支持向量。两个异类支持向量到超平面之间的距离之和,就是我们要找的间隔。
间隔有函数间隔和几何间隔,先讲函数间隔,设 f ( x ) = w T x + b f(x)=w^Tx+b f(x)=wTx+b,在超平面w*x+b=0确定的情况下, ∣ w ∗ x + b ∣ |w*x+b| ∣w∗x+b∣ 能够表示点x到距离超平面的远近,而通过观察 w ∗ x + b w*x+b w∗x+b 的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用 ( y ∗ ( w ∗ x + b ) ) (y*(w*x+b)) (y∗(w∗x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了函数间隔(functional margin)的概念。
定义函数间隔(用
γ
^
\widehat{\gamma }
γ
表示)为:
γ
^
=
y
(
w
T
x
+
b
)
=
y
f
(
x
)
\widehat{\gamma }=y(w^Tx+b)=yf(x)
γ
=y(wTx+b)=yf(x)
γ ^ \widehat{\gamma} γ 越大,代表可信度越高,但是函数间隔有问题,假如同时增大 w , b 到 k 倍 w,b 到k倍 w,b到k倍,超平面没有变,但是间隔函数值却改变了。
事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离–几何间隔(geometrical margin)的概念,

样本空间中任意一点
x
x
x到超平面
(
w
,
b
)
(w,b)
(w,b)的距离用
γ
\gamma
γ 表示,根据几何知识,上图中有
x
=
x
0
+
γ
w
∥
w
∥
w
T
x
0
+
b
=
0
w
T
w
=
∥
w
∥
2
x=x_0+\gamma\frac{w}{\left \| w \right \|} \\ w^Tx_0+b=0 \\ w^Tw={\left \| w \right \|}^2
x=x0+γ∥w∥wwTx0+b=0wTw=∥w∥2
根据上面3个式子即可求出
γ
=
w
T
x
+
b
∥
w
∥
\gamma=\frac{w^Tx+b}{\left \| w \right \|}
γ=∥w∥wTx+b
γ
\gamma
γ的绝对值
∣
γ
∣
=
∣
w
T
x
+
b
∣
∥
w
∥
=
y
(
w
T
x
+
b
)
∥
w
∥
=
y
f
(
x
)
∥
w
∥
|\gamma|=\frac{|w^Tx+b|}{\left \| w \right \|}=\frac{y(w^Tx+b)}{\left \| w \right \|}=\frac{yf(x)}{\left \| w \right \|}
∣γ∣=∥w∥∣wTx+b∣=∥w∥y(wTx+b)=∥w∥yf(x),也就是说,几何间隔等于函数间隔除以
∥
w
∥
\left \| w \right \|
∥w∥
前面我们收到两个异类支持向量到超平面的距离就是间隔,也就是
γ
=
2
∥
w
∥
\gamma=\frac{2}{\left \| w \right \|}
γ=∥w∥2
要找到“最大间隔”的划分超平面,也就是要找到能满足上式中约束的参数
w
和
b
w和b
w和b,使得
γ
\gamma
γ最大,即
m
a
x
w
,
b
2
∥
w
∥
s
.
t
.
y
i
(
w
T
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
.
.
.
,
m
\underset{w,b}{max} \ \frac{2}{\left \| w \right \|} \\ s.t. y_i(w^Tx_i+b)\geq1, \quad i=1,2,...,m
w,bmax ∥w∥2s.t.yi(wTxi+b)≥1,i=1,2,...,m
上式又可以重写为
m
i
n
w
,
b
1
2
∣
∣
w
∣
∣
2
s
.
t
.
y
i
(
w
T
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
.
.
.
,
m
\underset{w,b}{min}\ \frac{1}{2}\ ||w||^2 \\ s.t. y_i(w^Tx_i+b)\geq1, \quad i=1,2,...,m
w,bmin 21 ∣∣w∣∣2s.t.yi(wTxi+b)≥1,i=1,2,...,m
这就是支持向量机 ( S u p p o r t V e c t o r M a c h i n e , 简 称 S V M ) (Support Vector Machine,简称SVM) (SupportVectorMachine,简称SVM)的基本型。
搞懂对偶问题与KKT条件
前面我们得到了SVM的基本型,也就是目标函数,因为现在的目标函数是二次的,约束条件是线性的,所以它是一个凸二次规划问题。这个问题可以用现成的QP (Quadratic Programming) 优化包进行求解。一言以蔽之:在一定的约束条件下,目标最优,损失最小。
此外,由于这个问题的特殊结构,还可以通过拉格朗日对偶性(Lagrange Duality)变换到对偶变量 (dual variable) 的优化问题,即通过求解与原问题等价的对偶问题(dual problem)得到原始问题的最优解,这就是线性可分条件下支持向量机的对偶算法,这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
一般的,对于
m
i
n
f
(
x
)
s
.
t
.
h
j
(
x
)
=
0
j
=
1
,
2
,
.
.
.
p
g
k
(
x
)
≤
0
,
k
=
1
,
2...
q
min\ f(x) \\ s.t. h_j(x)=0\ j=1,2,...p\\g_k(x)\leq0,\ k=1,2...q
min f(x)s.t.hj(x)=0 j=1,2,...pgk(x)≤0, k=1,2...q
则我们定义不等式约束下的拉格朗日函数
L
L
L,则
L
L
L表达式为:
L
(
x
,
λ
,
μ
)
=
f
(
x
)
+
∑
j
=
1
p
λ
j
h
j
(
x
)
+
∑
k
=
1
q
μ
k
g
k
(
x
)
L(x,\lambda,\mu)=f(x)+\sum_{j=1}^{p}\ \lambda_jh_j(x)+\sum_{k=1}^{q}\ \mu_kg_k(x)
L(x,λ,μ)=f(x)+j=1∑p λjhj(x)+k=1∑q μkgk(x)
其
中
f
(
x
)
是
目
标
函
数
,
h
j
是
恒
等
式
约
束
,
λ
j
是
对
应
的
约
束
系
数
,
g
k
是
不
等
式
约
束
,
μ
k
是
对
应
的
约
束
系
数
其中f(x)是目标函数,h_j是恒等式约束,\lambda_j是对应的约束系数,g_k是不等式约束,\mu_k是对应的约束系数
其中f(x)是目标函数,hj是恒等式约束,λj是对应的约束系数,gk是不等式约束,μk是对应的约束系数。
KKT条件是说最优值必须满足以下条件:
1.
L
(
x
,
λ
,
μ
)
对
x
求
导
为
零
2.
h
(
x
)
=
0
;
3.
μ
∗
g
(
x
)
=
0
1. L(x,\lambda ,\mu )对x求导为零\\ 2.h(x) =0;\\ 3. \mu*g(x) = 0
1.L(x,λ,μ)对x求导为零2.h(x)=0;3.μ∗g(x)=0
前面两个条件比较容易理解,下面我们讲具体说明KKT条件的第三个条件,这里讲
L
L
L函数简化为
L
(
x
,
μ
)
=
f
(
x
)
+
∑
k
=
1
q
μ
k
g
k
(
x
)
L(x,\mu)=f(x)+\sum_{k=1}^{q}\ \mu_kg_k(x)
L(x,μ)=f(x)+k=1∑q μkgk(x)
此时有,
∵
μ
≥
0
,
g
k
(
x
)
≤
0
∴
μ
g
(
x
)
≤
0
∴
m
a
x
μ
L
(
x
,
μ
)
=
f
(
x
)
∴
m
i
n
x
f
(
x
)
=
m
i
n
x
m
a
x
μ
L
(
x
,
μ
)
(
1
)
\because \ \mu \geq0,g_k(x)\leq0 \\ \therefore \ \mu g(x)\leq0 \\ \therefore \ \underset{\mu}{max} \ L(x,\mu)=f(x) \\ \therefore \underset{x}{min}\ f(x)=\underset{x}{min} \ \underset{\mu}{max} \ L(x,\mu) \qquad(1)
∵ μ≥0,gk(x)≤0∴ μg(x)≤0∴ μmax L(x,μ)=f(x)∴xmin f(x)=xmin μmax L(x,μ)(1)
反过来看一下
m
a
x
μ
m
i
n
x
L
(
x
,
μ
)
=
m
a
x
μ
[
m
i
n
x
f
(
x
)
+
m
i
n
x
μ
g
(
x
)
]
=
m
a
x
μ
m
i
n
x
f
(
x
)
+
m
a
x
μ
m
i
n
x
μ
g
(
x
)
\underset{\mu}{max} \ \underset{x}{min} \ L(x,\mu)=\underset{\mu}{max} \ [\underset{x}{min} \ f(x)+\underset{x}{min} \ \mu g(x)]\\=\underset{\mu}{max} \ \underset{x}{min} \ f(x)+\underset{\mu}{max} \ \underset{x}{min} \ \mu g(x)
μmax xmin L(x,μ)=μmax [xmin f(x)+xmin μg(x)]=μmax xmin f(x)+μmax xmin μg(x)
此时,
m
a
x
μ
m
i
n
x
f
(
x
)
=
m
i
n
x
f
(
x
)
\underset{\mu}{max} \ \underset{x}{min} \ f(x)=\underset{x}{min} \ f(x)
μmax xmin f(x)=xmin f(x),因为
f
(
x
)
与
μ
无
关
f(x)与\mu无关
f(x)与μ无关,而
∵
μ
g
(
x
)
≤
0
∴
m
i
n
x
μ
g
(
x
)
=
{
0
,
μ
=
0
∣
∣
g
(
x
)
=
0
−
∞
,
μ
>
0
&
g
(
x
)
<
0
∴
m
a
x
μ
m
i
n
x
μ
g
(
x
)
=
0
,
μ
=
0
∣
∣
g
(
x
)
=
0
\because\ \mu g(x)\leq0 \\\therefore \ \underset{x}{min} \ \mu g(x)=\left\{\begin{matrix} 0,& \mu=0 \ ||\ g(x)=0\\ -\infty,& \mu>0 \ \& \ g(x)<0 \end{matrix}\right.\\ \therefore \ \underset{\mu}{max} \ \underset{x}{min} \ \mu g(x)=0,\ \mu=0 \ ||\ g(x)=0
∵ μg(x)≤0∴ xmin μg(x)={0,−∞,μ=0 ∣∣ g(x)=0μ>0 & g(x)<0∴ μmax xmin μg(x)=0, μ=0 ∣∣ g(x)=0
所以可以得出 m a x μ m i n x L ( x , μ ) = m i n x f ( x ) , μ g ( x ) = 0 , μ = 0 ∣ ∣ g ( x ) = 0 ( 2 ) \underset{\mu}{max} \ \underset{x}{min} \ L(x,\mu)= \underset{x}{min} \ f(x), \ \mu g(x)=0,\ \mu=0 \ ||\ g(x)=0 \qquad(2) μmax xmin L(x,μ)=xmin f(x), μg(x)=0, μ=0 ∣∣ g(x)=0(2)
由公式(1),(2)可得
m
a
x
μ
m
i
n
x
L
(
x
,
μ
)
=
m
i
n
x
m
a
x
μ
L
(
x
,
μ
)
s
.
t
.
μ
g
(
x
)
=
0
μ
≥
0
\underset{\mu}{max} \ \underset{x}{min} \ L(x,\mu)=\underset{x}{min} \ \underset{\mu}{max} \ L(x,\mu)\\ s.t.\ \mu g(x)=0\\ \mu \geq0
μmax xmin L(x,μ)=xmin μmax L(x,μ)s.t. μg(x)=0μ≥0
此时极小极大问题就转变成了极大极小问题,我们称,极大极小问题是原问题的对偶问题,条件就是KKT条件。
那么回到SVM的目标函数来,
m
i
n
w
,
b
1
2
∣
∣
w
∣
∣
2
s
.
t
.
y
i
(
w
T
x
i
+
b
)
≥
1
,
i
=
1
,
2
,
.
.
.
,
m
\underset{w,b}{min}\ \frac{1}{2}\ ||w||^2 \\ s.t.\ y_i(w^Tx_i+b)\geq1, \quad i=1,2,...,m
w,bmin 21 ∣∣w∣∣2s.t. yi(wTxi+b)≥1,i=1,2,...,m
根据上面的结论,求SVM的目标函数
m
i
n
min
min最优等价于求
m
a
x
α
m
i
n
w
,
b
L
(
w
,
b
,
α
)
\ \underset{\alpha }{max} \ \underset{w,b}{min} \ L(w,b,\alpha )
αmax w,bmin L(w,b,α),其中
L
L
L为该目标函数的拉格朗日函数,可写为
L
(
w
,
b
,
α
)
=
1
2
∣
∣
w
∣
∣
2
+
∑
i
=
1
m
α
i
(
1
−
y
i
(
w
T
x
i
+
b
)
L(w,b,\alpha )= \frac{1}{2}\ ||w||^2+\sum_{i=1}^{m}\ \alpha _i(1-y_i(w^Tx_i+b)
L(w,b,α)=21 ∣∣w∣∣2+i=1∑m αi(1−yi(wTxi+b)
之后就是求解对偶问题 L L L,
1.先对 w 和 b w和b w和b求偏导

将以上结果代入之前的
L
L
L,得


其具体推导过程比较复杂,如下图所示

对 α \alpha α求极大。根据 w = ∑ i = 1 m α i y i x i w=\sum_{i=1}^{m}\ \alpha_iy_ix_i w=∑i=1m αiyixi,即可求出 b b b,最终得出分离超平面和分类决策函数。
3.在求得 L ( w , b , α ) L(w, b, \alpha) L(w,b,α)关于 w w w 和 $b $最小化,以及 α \alpha α对的极大之后,最后一步则可以利用SMO算法求解对偶问题中的拉格朗日乘子 α \alpha α,具体的解法可以查看这个博客
搞懂核函数 K e r n e l Kernel Kernel
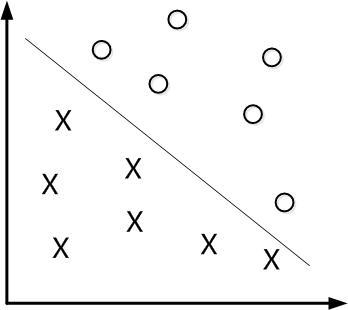
到目前为止,我们的 SVM 还比较弱,只能处理线性可分的情况,而现实任务中,原始样本空间内也许并不存在一个能够正确划分两类样本的超平面,对于下图的问题就不是线性可分的。
具体来说,在线性不可分的情况下,支持向量机首先在低维空间中完成计算,然后通过核函数将输入空间映射到高维特征空间,最终在高维特征空间中构造出最优分离超平面,从而把平面上本身不好分的非线性数据分开。
令
ϕ
(
x
)
\phi(x)
ϕ(x)表示将
x
x
x映射后的特征向量,于是,在特征空间中划分超平面所对应的模型可表示为
f
(
x
)
=
w
T
ϕ
(
x
)
+
b
f(x)=w^T\phi(x)+b
f(x)=wTϕ(x)+b
其中
w
和
b
w和b
w和b是模型参数,类似的,有
m
i
n
w
,
b
1
2
∣
∣
w
∣
∣
2
s
.
t
.
y
i
(
w
T
ϕ
(
x
i
)
+
b
)
≥
1
,
i
=
1
,
2
,
.
.
.
,
m
\underset{w,b}{min}\ \frac{1}{2}\ ||w||^2 \\ s.t.\ y_i(w^T\phi(x_i)+b)\geq1, \quad i=1,2,...,m
w,bmin 21 ∣∣w∣∣2s.t. yi(wTϕ(xi)+b)≥1,i=1,2,...,m
其对偶问题是
m
a
x
α
∑
i
=
1
m
−
1
2
∑
i
=
1
m
∑
j
=
1
m
α
i
α
j
y
i
y
j
ϕ
(
x
i
)
T
ϕ
(
x
j
)
s
.
t
.
∑
i
=
1
m
α
i
y
i
=
0
,
α
i
≥
,
i
=
1
,
2
,
.
.
.
,
m
\underset{\alpha}{max}\ \sum_{i=1}^{m}-\frac{1}{2}\ \sum_{i=1}^{m}\sum_{j=1}^{m}\ \alpha_i\alpha_jy_iy_j\phi(x_i)^T\phi(x_j)\\ s.t.\ \sum_{i=1}^{m}\ \alpha_iy_i=0,\\ \alpha_i \geq, \quad i=1,2,...,m
αmax i=1∑m−21 i=1∑mj=1∑m αiαjyiyjϕ(xi)Tϕ(xj)s.t. i=1∑m αiyi=0,αi≥,i=1,2,...,m
求解上式涉及到计算
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\phi(x_i)^T\phi(x_j)
ϕ(xi)Tϕ(xj),这是样本
x
i
与
x
j
x_i与x_j
xi与xj映射到特征空间之后的内积。由于特征空间是高纬度的,甚至是无穷维,因此计算
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\phi(x_i)^T\phi(x_j)
ϕ(xi)Tϕ(xj)通常是困难的,为了避免这个障碍,可以设想这样的一个函数
κ
(
x
i
,
x
j
)
=
⟨
ϕ
(
x
i
)
,
ϕ
(
x
j
)
⟩
=
ϕ
(
x
i
)
T
ϕ
(
x
j
)
\kappa (x_i,x_j)=\left \langle\phi(x_i),\phi(x_j) \right \rangle=\phi(x_i)^T\phi(x_j)
κ(xi,xj)=⟨ϕ(xi),ϕ(xj)⟩=ϕ(xi)Tϕ(xj)
这里的
κ
(
⋅
,
⋅
)
\kappa(\cdot,\cdot)
κ(⋅,⋅)就是“核函数”,一个是映射到高维空间中,然后再根据内积的公式进行计算;而另一个则直接在原来的低维空间中进行计算,而不需要显式地写出映射后的结果。
这就是为什么上文说:这样做的优点在于:一者对偶问题往往更容易求解;二者可以自然的引入核函数,进而推广到非线性分类问题。
显然,已知合适的映射 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅)的具体形式,则可以写出核函数 κ ( ⋅ , ⋅ ) \kappa(\cdot,\cdot) κ(⋅,⋅)但在现实 任务中我们通常不知道 ϕ ( ⋅ ) \phi(\cdot) ϕ(⋅) 是什么形式,那么,合适的核函数是否一定存在呢? 什么样的函数能做核函数呢?我们有下面的定理:
令
X
X
X 为输入空间,
κ
(
⋅
,
⋅
)
\kappa(\cdot,\cdot)
κ(⋅,⋅) 是定义在
X
×
X
X \times X
X×X 上的对称函数,则
κ
\kappa
κ 是核函数当且仅当对于任意数据
D
=
x
1
,
x
2
,
.
.
.
x
m
D = {x_1, x_2,...x_m}
D=x1,x2,...xm,“核矩阵”
(
k
e
r
n
e
l
m
a
t
r
i
x
)
(kernel matrix)
(kernelmatrix)
K
K
K 总是半正定的:
也就是说,只要一个对称函数所对应的核矩阵半正定,它就能作为核 函数使用.事实上,对于一个半正定核矩阵,总能找到一个与之对应的映射
ϕ
\phi
ϕ. 换言之,任何一个核函数都隐式地定义了一个称为"再生核希尔伯特空间"
(
R
e
p
r
o
d
u
c
i
n
g
K
e
r
n
e
l
H
i
l
b
e
r
t
S
p
a
c
e
,
简
称
R
K
H
S
)
(Reproducing Kernel Hilbert Space,简称 RKHS)
(ReproducingKernelHilbertSpace,简称RKHS)的特征空间.
通过前面的讨论可知,我们希望样本在特征空间内线性可分,因此特征空间的好坏对支持向量机的性能至关重要,需注意的是,在不知道特征映射的形式时,我们并不知道什么样的核函数是合适的,而核函数也仅是隐式地走义了这个特征空间.于是,"核函数选择"成为支持向量机的最大变数,若核函数选择不合适,则意味着将样本映射到了一个不合适的特征空间,很可能导致性能不佳。
常用的核函数,
后续
在前面的讨论中,我们一直假定训练样本在样本空间或特征空间中是线性可分的,即存在一个超平面能将不同类的样本完全划分开。然而,在现实任务中往往很难确定合适的核函数使得训练样本在特征空间中线性可分;退一步说,即使恰好找到了某个核函数使训练集在特征空间中线性可分,也很难断定这个貌似线性可分的结果不是由于过拟合所造成的。
缓解该问题的一个办法是允许支持向量机在一些样本上出错。为此,要引入"软间隔" ( s o f t m a r i n ) . (soft marin). (softmarin).的概念。
本文到此结束,请读者随时批评指正,感谢
参考文献及推荐阅读
1.持向量机通俗导论(理解SVM的三层境界)
2.《机器学习》.周志华著






















 1690
1690











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








