A Survey on Mixture of Experts 混合专家模型综述(第一部分：混合专家算法设计)

Phoenixtree_DongZhao

已于 2025-03-14 21:21:17 修改

阅读量971

点赞数 30

分类专栏：混合专家 MoE Large Model 文章标签： MoE 大模型混合专家

于 2025-03-14 16:53:58 首次发布

本文链接：https://blog.csdn.net/u014546828/article/details/146247411

版权

Large Model 同时被 2 个专栏收录

52 篇文章

订阅专栏

混合专家 MoE

7 篇文章

订阅专栏

A Survey on Mixture of Experts 混合专家模型综述

(第二部分：混合专家系统设计)

A Survey on Mixture of Experts

arxiv

github：A-Survey-on-Mixture-of-Experts-in-LLMs

Abstract

Large language models (LLMs) have garnered unprecedented advancements across diverse fields, ranging from natural language processing to computer vision and beyond. The prowess of LLMs is underpinned by their substantial model size, extensive and diverse datasets, and the vast computational power harnessed during training, all of which contribute to the emergent abilities of LLMs (e.g., in-context learning) that are not present in small models. Within this context, the mixture of experts (MoE) has emerged as an effective method for substantially scaling up model capacity with minimal computation overhead, gaining significant attention from academia and industry. Despite its growing prevalence, there lacks a systematic and comprehensive review of the literature on MoE. This survey seeks to bridge that gap, serving as an essential resource for researchers delving into the intricacies of MoE. We first briefly introduce the structure of the MoE layer, followed by proposing a new taxonomy of MoE. Next, we overview the core designs for various MoE models including both algorithmic and systemic aspects, alongside collections of available open-source implementations, hyperparameter configurations and empirical evaluations. Furthermore, we delineate the multifaceted applications of MoE in practice, and outline some potential directions for future research.

大型语言模型（LLMs）在自然语言处理、计算机视觉等众多领域取得了前所未有的突破性进展。其强大能力源于庞大的模型规模、海量多样化的数据集以及训练过程中调用的巨量算力，这些要素共同催生了小模型所不具备的涌现能力（例如上下文学习）。在此背景下，混合专家（Mixture of Experts, MoE）因其能以极低计算开销实现模型容量的大规模扩展而成为重要技术路径，受到学术界与工业界的广泛关注。尽管MoE的应用日益普及，目前仍缺乏对其研究文献的系统性综述。本调查旨在填补这一空白，为深入探索MoE技术的研究者提供核心参考资源。我们首先简要介绍MoE层的结构设计，进而提出新的MoE技术分类体系。随后，从算法架构与系统实现两个维度综述各类MoE模型的核心设计范式，并整理开源实现方案、超参数配置与实证评估结果。此外，本文梳理了MoE在实践中的多领域应用场景，最后指出未来研究的潜在发展方向。

1. Introduction

In the current landscape of artificial general intelligence (AGI), the transformative impact of transformer-based large language models (LLMs) has permeated diverse fields such as natural language processing [1], [2], [3], [4], [5], [6], [7], computer vision [8], [9], and multimodality [10], [11], [12], [13]. Building upon the foundational transformer architecture, LLMs demonstrate extraordinary capabilities, which are attributed to their sheer size, the breadth of data they are trained on, and the significant computational resources invested in their development [14], [15], [16]. Recognizing a scaling law [14], [17] that underpins their evolution, it is imperative to identify and implement efficient methodologies for the sustainable scaling of LLMs.

The concept of mixture of experts (MoE), initially introduced in [18], [19], has undergone extensive exploration and advancement as evidenced by subsequent studies [20], [21], [22], [23], [24], [25], [26]. The emergence of sparsely-gated MoE [27], particularly within the integration of transformerbased large language models [28], has brought new vitality to this three-decade-old technology. The MoE framework is based on a simple yet powerful idea: different parts of a model, known as experts, specialize in different tasks or aspects of the data. With this paradigm, only pertinent experts are engaged for a given input, keeping the computational cost in check while still benefiting from a large pool of specialized knowledge. This scalable and flexible innovation has offered an effective approach for adhering to the scaling law, allowing for increased model capacity without a corresponding surge in computational demands. As depicted in Figure 1, MoE has maintained a robust trajectory of growth, particularly notable in 2024 with the advent of Mixtral-8x7B [29] and a variety of subsequent industrial-scale LLMs such as Grok-1 [30], DBRX [31], Arctic [32], DeepSeek-V2 [33], etc.

在当前通用人工智能（AGI）的发展格局中，基于Transformer架构的大型语言模型（LLMs）已展现出革命性影响力，其触角延伸至自然语言处理、计算机视觉及多模态领域等多样化场景。依托Transformer架构的基石，LLMs凭借庞大的参数量级、海量训练数据与训练阶段投入的巨量算力资源，展现出非凡的智能涌现能力。研究表明，LLMs的演进遵循可量化的扩展定律（scaling law），这使得探索高效且可持续的模型扩展方法论成为关键课题。

混合专家（Mixture of Experts, MoE）这一概念最早可追溯至的开创性工作，后续研究对其进行了深入探索与改进。稀疏门控MoE（sparsely-gated MoE）的提出，尤其是其与Transformer架构的深度融合，为这项已有三十年历史的技术注入了新生机。

MoE的核心思想简洁而强大：

模型的不同部分（即专家网络）专注于处理特定任务或数据特征，通过动态激活与输入相关的专家子集，既能利用大规模专家池的专业知识，又能有效控制计算开销。

这种可扩展的灵活设计为遵循扩展定律提供了有效路径，使得模型容量的提升不再伴随计算需求的线性增长。如图1所示，MoE技术发展势头强劲，2024年Mixtral-8x7B的发布更标志着其进入工业级应用阶段，后续涌现出Grok-1、DBRX、Arctic、DeepSeek-V2等系列工业级LLMs。

Despite the increasing popularity and application of MoE models in various domains, the literature has yet to see a survey that thoroughly examines and categorizes the advancements in this area. The most recent review of MoE we could find was presented in September 2022 [34], predating the pivotal “ChatGPT moment”, which omits the significant advancements that have recently emerged alongside the escalating academic and industrial interest in this domain. This gap in the literature not only hinders the progress of MoE research but also limits the dissemination of knowledge on this topic to a broader audience. Our survey aims to address this deficit by providing a clear and comprehensive overview of MoE with a novel taxonomy that segments recent progress into algorithm, system, and application.

Under this taxonomy, we first delve into MoE algorithmic advancements, particularly the prevalent substitution of feed-forward network (FFN) layers with MoE layers in transformer-based LLMs [28], [29], [33], [35], [36], [37], [38]. As each MoE layer integrates multiple FFNs—each designated as an expert—and employs a gating function to activate a selected subset of these experts, we explore the design choices of gating function and expert network, alongside collections of available open-source implementations, hyperparameter configurations, and empirical evaluations. Furthermore, to underscore the flexibility and versatility of MoE, we extend our analysis beyond the standard integration of MoE into model backbone, and discuss an array of novel MoE-related designs, such as soft MoE with token or expert merging [39], [40], [41], [42], [43], mixture of parameter-efficient experts (MoPEs) [42], [44], [45], [46], [47],[48], training and inference schemes with model transition between dense and sparse [49], [50], [51], [52], [53], [54], and various derivatives [55], [56], [57], [58], [59], [60].

尽管MoE模型在多领域应用日益广泛，学界仍缺乏对其最新进展的系统性梳理与分类。现有最新综述可追溯至2022年9月，彼时尚未经历"ChatGPT时刻"的突破性进展，亦未涵盖近年来学术界与工业界对该领域的高度关注催生的重大创新。这一文献空白不仅制约了MoE研究的深化，也阻碍了相关知识的广泛传播。本综述旨在填补这一缺口，通过提出算法-系统-应用三维分类法，对MoE技术进行全面梳理。

在此分类框架下，我们首先聚焦算法创新。当前主流方案将Transformer架构中的前馈网络（FFN）层替换为MoE层，每个MoE层包含多个专家网络（即FFN）及门控函数（gating function）以动态选择激活的专家子集。本文系统探讨门控函数与专家网络的设计选择，并整理开源实现方案、超参数配置与实证评估结果。为进一步彰显MoE的灵活性，我们突破传统模型主干集成范式，深入分析软性MoE（soft MoE）（通过标记/专家融合实现参数共享）、参数高效混合专家（MoPEs）（结合参数高效微调技术）、稠密-稀疏动态切换的训练与推理机制，以及各类衍生架构等前沿方向。

With the gradual convergence of model architecture design in industrial products, system design has emerged as a pivotal factor in enhancing the quality of LLM services. Given the close association of MoE models with machine learning system design, we provide a comprehensive overview of MoE system design, including computation, communication, and storage enhancements tailored to address the unique challenges posed by the sparse and dynamic nature of its computational workload. Additionally, we overview the applications of MoE across various domains, including natural language processing, computer vision, recommender system, and multimodal contexts.

The remainder of this survey is organized as follows. Section 2 provides a foundational understanding of MoE, contrasting sparse and dense activation of experts. Section 3 introduces our proposed taxonomy for categorizing MoE advancements. Sections 4, 5, and 6 delve into the algorithmic designs, computing system support, and various applications of MoE models, respectively, following the structure outlined in our taxonomy in Figure 3. Finally, in Section 7, we highlight the critical challenges and opportunities for bridging the research-practicality gap, culminating in Section 8 with our conclusions.

随着工业级产品中模型架构设计的日趋收敛，系统优化已成为提升LLM服务质量的关键要素。针对MoE模型计算负载的稀疏性与动态性特征，本文从计算加速、通信优化与存储管理三方面系统综述专用系统设计，剖析其应对独特挑战的创新方案。此外，我们全面梳理MoE在自然语言处理、计算机视觉、推荐系统及多模态场景等领域的应用实践。

本文结构安排如下：第2章解析MoE基础原理，对比稀疏激活与稠密激活范式；第3章提出三维分类法；第4-6章依循图3所示框架，分别深入探讨算法设计、系统支持与应用场景；第7章聚焦研究与实践的鸿沟，剖析关键挑战与机遇；第8章总结全文。

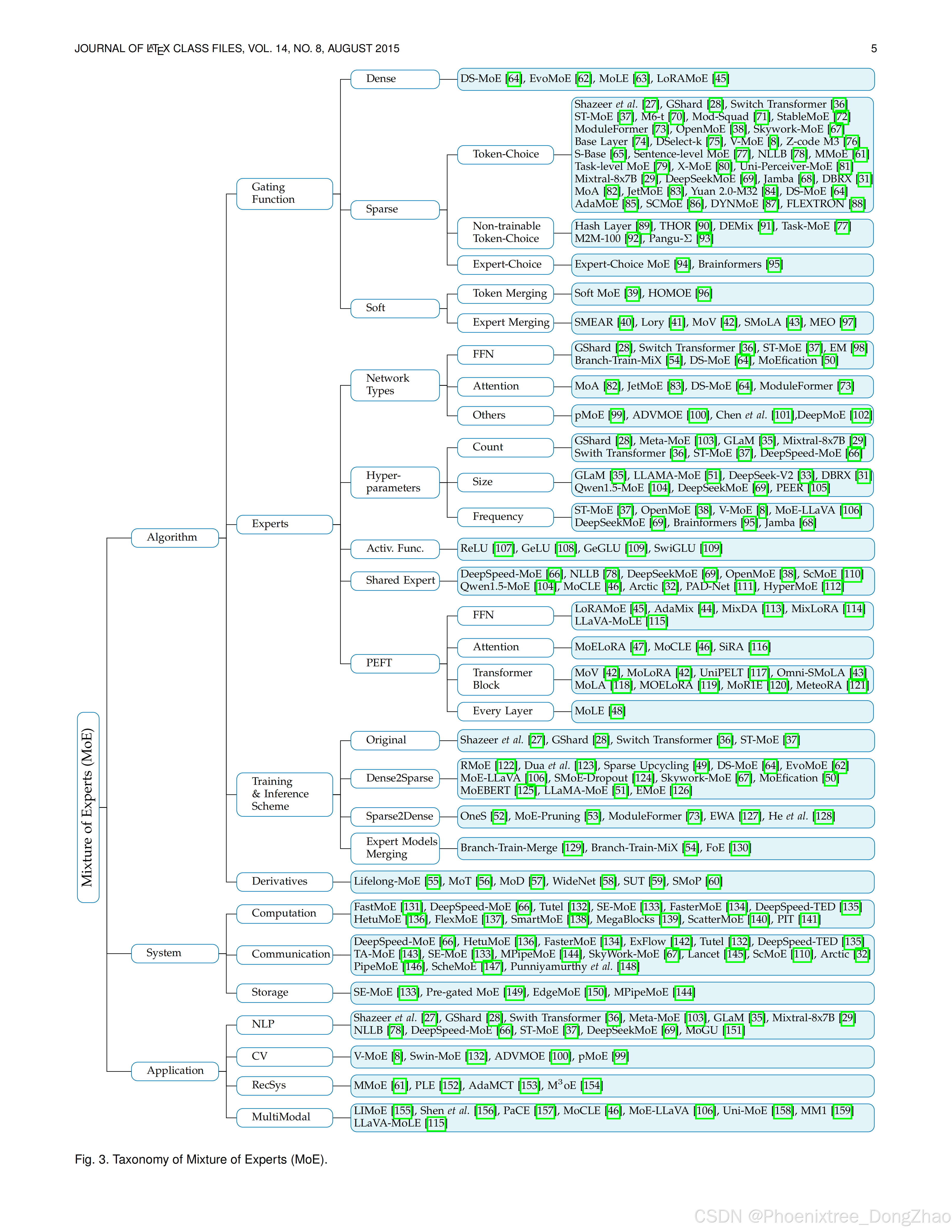
3. Taxonomy of Mixture of Experts 混合专家分类法

To effectively scale model parameters without a corresponding increase in computational demand, the mixture of experts (MoE) architecture has emerged as a viable solution. MoE leverages a collection of specialized models and a gating mechanism to dynamically select the appropriate “expert networks” for processing a given input. This enables the model to allocate computational resources on an asneeded basis, a concept known as conditional computation. The incorporation of MoE architectures into large language models (LLMs) is now a prevalent practice, allowing these models to achieve significant parameter scale-ups and consequent enhancements in capabilities [28], [29], [34], [36], [67].

For example, the Mixtral 8x7B [29], introduced by Mixtral AI, shares its foundational architecture with the earlier Mistral 7B [160], but with a notable difference: each layer comprises eight feed-forward networks (FFN) (i.e., experts). Despite utilizing only 13 billion active parameters, the Mixtral-8x7B demonstrates superior or equivalent performance to the Llama-2-70B [161] and GPT-3.5 [162] across various benchmarks. Similarly, the DeepSeek LLM [163], developed by DeepSeek, has been extended with an MoE variant known as DeepSeekMoE [69]. The DeepSeekMoE 16B, while requiring approximately 40% less computation, attains performance on par with the Llama 2 7B [161]. The Qwen team has also contributed to this innovative field by developing the Qwen1.5-MoE [104], a smaller MoE model with only 2.7B active parameters that rivals the performance of leading 7B parameter models such as the Mistral 7B [160] and the Qwen1.5-7B [164].

To assist researchers in navigating the rapidly evolving landscape of LLMs equipped with MoE architectures, we have developed a taxonomy that categorizes these models from three perspectives: algorithm design, system design, and application. Figure 3 showcases our taxonomy alongside several representative studies. In the following sections, we provide a comprehensive and in-depth analysis of each category within our taxonomy.

为实现模型参数的高效扩展而无需对应增加计算需求，混合专家（Mixture of Experts, MoE）架构已成为可行解决方案。MoE通过集成多个专业化子模型（专家网络）与动态门控机制，根据输入特征选择激活相关专家，实现按需分配计算资源的条件计算（conditional computation）范式。当前，将MoE架构融入大型语言模型（LLMs）已成为主流实践，显著提升模型参数量级与能力边界。

例如，Mixtral AI推出的Mixtral 8x7B模型延续了Mistral 7B的基础架构，但每层引入8个前馈网络（FFN）作为专家网络。尽管仅激活130亿参数，其在多项基准测试中性能超越或持平Llama-2-70B与GPT-3.5。DeepSeek团队开发的DeepSeek LLM亦衍生出MoE变体DeepSeekMoE，其DeepSeekMoE 16B模型在减少约40%计算量的前提下，性能与Llama 2 7B相当。阿里云Qwen团队推出的Qwen1.5-MoE更是以仅27亿激活参数量，达到Mistral 7B、Qwen1.5-7B等主流7B参数模型的性能水平。

为助力研究者系统把握MoE增强型LLMs的快速发展脉络，本文提出三维分类法，从算法设计、系统优化与应用场景三个维度对相关模型进行归类梳理。图3展示了该分类框架及代表性研究工作。下文将依此分类体系，对各分支展开深入解析。

4. Algorithm Design of Mixture of Experts

4.1 Gating Function

The gating function (also known as the routing function or router), which stands as a fundamental component of all the MoE architectures, orchestrates the engagement of expert computations and the combination of their respective outputs. We categorize this mechanism into three distinct types Based on the processing methodologies of each input, we categorize the gating mechanism into three distinct types: sparse, which activates a subset of experts; dense, which activates all experts; and soft, which encompasses fullydifferentiable approaches including input token merging and expert merging.

4.1 门控函数

门控函数（又称路由函数或路由器）作为所有混合专家（MoE）架构的基础组件，负责协调专家计算资源的调度及其输出结果的融合。根据每个输入的处理方式，我们将门控机制分为三种类型：稀疏门控（仅激活部分专家）、稠密门控（激活所有专家）和软性门控（包含完全可微分的方法，如输入令牌融合与专家融合）。

4.1.1 Sparse;

4.1.2 Dense;

4.1.3 Soft.

4.1.1 Sparse

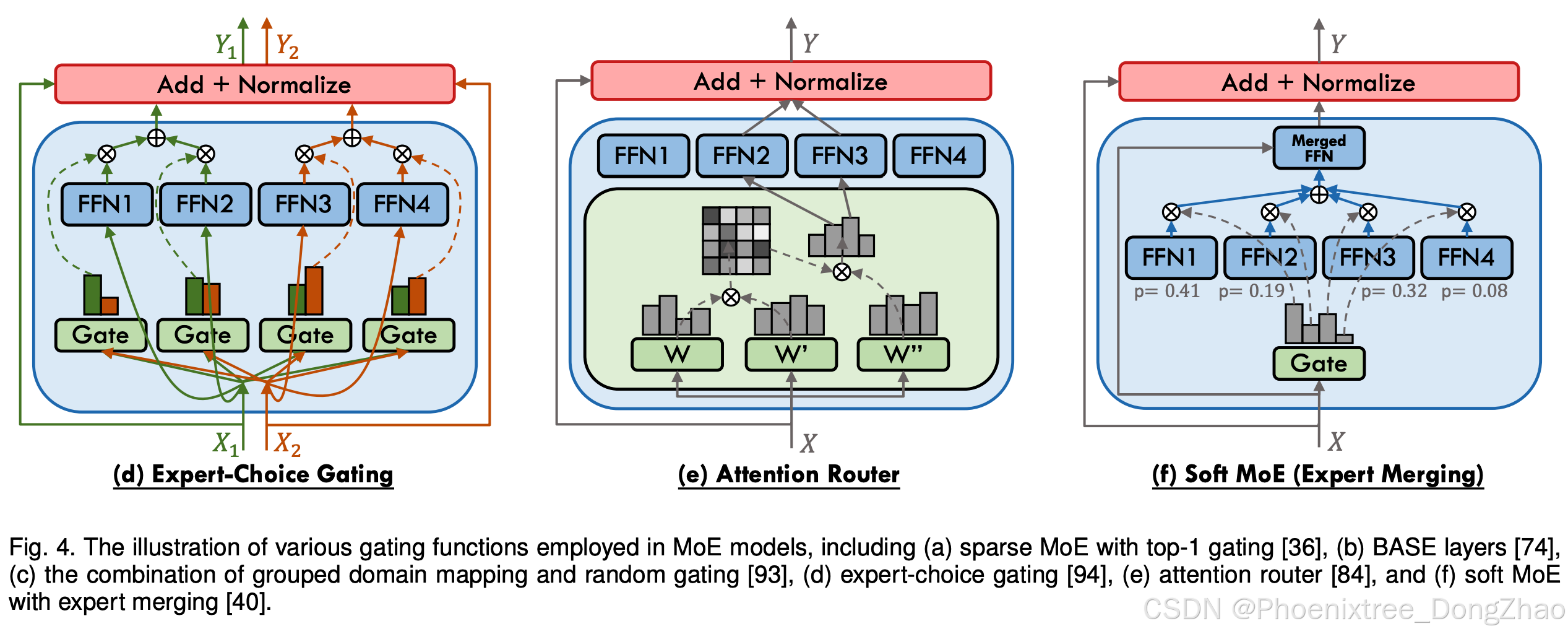
The sparse gating functions activate a selected subset of experts for processing each individual input token, which can be considered as a form of conditional computation [165], [166], [167]. The gating functions have been studied extensively, which may be trained by various forms of reinforcement learning and back-propagation, making binary or sparse and continuous, stochastic or deterministic gating decisions [23], [65], [168], [169], [170]. Shazeer et al. [27] pioneered a differentiable heuristic with auxiliary load balancing losses, in which the outputs from expert computations are weighted by their selection probabilities. This introduces a differentiable aspect to the gating process, thereby facilitating the derivation of gradients that can guide the gating function’s optimization. This paradigm has subsequently become predominant in the realm of MoE research. Due to its selection of experts for each input token, this method can be recognized as a gating function with token choice.

4.1.1 稀疏门控

稀疏门控函数为每个输入令牌激活选定的专家子集进行处理，这可以被视为一种条件计算形式。门控函数的研究已较为深入，其训练可通过强化学习、反向传播等多种方法实现，支持二值化/稀疏化、连续化、随机化或确定性化的门控决策。Shazeer等人率先提出了一种结合辅助负载均衡损失的可微分启发式方法，通过专家选择概率加权专家计算的输出。这种方法为门控过程引入可微分性，从而支持通过梯度优化门控函数。该范式随后成为MoE研究的主流。由于其为每个输入令牌选择专家，该方法可视为一种基于令牌选择的门控函数。

Token-Choice Gating.

Shazeer et al. [27] posited the necessity of gating inputs to the top-k experts, with k > 1, to enhance the efficacy of MoE. The rationale behind this approach is that by simultaneously consulting multiple experts for a given input, the network can effectively weigh and integrate their respective contributions, thereby improving performance. To accommodate the scalability to thousands of experts within a MoE layer, they employ a two-level hierarchical MoE to reduce the branching factor in the context of a large expert count. Subsequent research has largely affirmed that increasing the value of k enhances performance, which has led to the widespread adoption of this top-k strategy with k > 1. Notwithstanding, the Switch Transformer model [36] has shown that a top-1 gating strategy (as illustrated in Figure 4 (a)) can also yield competitive results, a finding that has been substantiated and adopted by later studies [65]. Furthermore, M6-t [70] proposed a novel variation of the top-1 gating called expert prototyping, which organizes experts into k groups and then applies top-1 gating in each group. Their experimental results show the training and downstream perplexity of a 16-layer model in order of best to worst: expert prototyping with 4 top-1 gating, 1 top-4 gating, 1 top-16 gating, 1 top-1 gating.

基于令牌选择的门控

Shazeer等人提出需通过top-k（k > 1）门控选择专家以提升MoE效能。其核心思想是通过同时调用多个专家，网络能有效权衡并整合不同专家的贡献以优化性能。为支持MoE层中数千级专家的扩展，他们采用双层级联MoE结构来降低大规模专家分支的复杂度。后续研究普遍证实增大k值能提升性能，这推动了k > 1的top-k策略广泛应用。然而，Switch Transformer模型表明top-1门控（如图4(a)）同样具有竞争力，这一结论被后续研究验证并采纳。此外，M6-t提出"专家原型化"的top-1门控变体：将专家分为k组后对各组实施top-1门控。实验显示，16层模型的训练与下游任务困惑度排序为：4组top-1 > 单组top-4 > 单组top-16 > 单组top-1。

Auxiliary Loss for Token-Choice Gating.

Token-choice gating algorithms frequently incorporate an auxiliary loss during training to promote equitable token distribution across experts. Table 1 shows prevalent auxiliary loss functions leveraged in the field. Shazeer et al. [27] quantify the importance of an expert in relation to a training batch via the batchwise sum of the gate values for that expert. They define an additional loss Limportance, added to the overall loss function for the model. This loss, which is equal to the square of the coefficient of variation of the set of importance values and multiplied by a hand-tuned scaling factor wimportance, encourages all experts to have equal importance. Although Limportance promotes balance in importance, it does not guarantee an even distribution of training examples among experts, which can lead to execution inefficiencies on distributed computing environments. To address this, they introduce a second loss Lload to ensure balanced loads. Building on this foundation, GShard [28] define a new differentiable auxiliary loss Laux using a differentiable approximation (the dot-product of mean gates and mean gating decisions per expert), as detailed in Section 2.2. Switch Transformers [36] and many other subsequent studies [29], [31], [35], [68] have embraced this Laux design, and enhancements [33], [67], [69] have been made to cater to diverse requirements. Nevertheless, ST-MoE [37] identified limitations with Laux, particularly at larger scales, leading to unreliable training outcomes. To mitigate this, it introduces the integration of router z-loss Lz, improving training stability without quality degradation by penalizing large logits entering the gating network. Since this loss encourages absolute magnitude of values to be smaller, roundoff errors are reduced, which can be quite impactful for exponential functions such as gating. Additionally, ModSquad [71] posits the difficulty of training multi-task models under such an expert-balancing loss, which may inadvertently force experts to set parameters on conflicting tasks or hinder the potential synergies from parameter sharing across complementary tasks. Instead, it proposes to maximize the mutual information (MI) between experts and tasks to build task-expert alignment. Differently, ModuleFormer [73] proposes to maximize the Mutual Information between experts and tokens. Furthermore, DS-MoE [64] extends the application of LM I , calibrating different weightings wM I , in Mixture-of-Attention (MoA, as illustrated in Figure 5 (a)) and FFN MoE modules of different size models.

令牌选择门控的辅助损失

基于令牌选择的门控算法常引入辅助损失以促进专家间的令牌均衡分配（常用辅助损失函数见表1）。Shazeer等人通过专家门控值的批次求和定义重要性指标，并设计辅助损失L_importance（重要性变异系数平方乘以手动调优权重W_importance），促使专家重要性均等化。但重要性均衡不等价于训练样本均衡分布，可能导致分布式计算效率问题，因此他们额外引入负载均衡损失Lload。GShard在此基础上提出可微分辅助损失Laux（通过门控均值与专家决策均值的点积近似），详见2.2节。Switch Transformers及后续研究[29][31][35][68]均采用Laux，并针对不同需求进行改进。然而，ST-MoE发现Laux在大规模场景下存在局限性，导致训练不稳定，因此引入惩罚门控网络大对数输入的Lz损失以提升稳定性。该损失通过抑制数值量级降低了指数运算的舍入误差。此外，ModSquad指出专家均衡损失可能迫使专家处理冲突任务或阻碍跨任务参数共享的协同效应，转而提出通过最大化专家与任务间的互信息（MI）实现对齐。ModuleFormer则提出最大化专家与令牌间的互信息。DS-MoE进一步扩展MI损失的应用，在不同规模的混合注意力（MoA，见图5(a)）和FFN MoE模块中校准权重WMI。

Expert Capacity for Token-Choice Gating.

In conjunction with load balancing via auxiliary loss, GShard [28] incorporates an expert capacity limit, defining a threshold for the number of tokens an expert can process. This can lead to token overflow, where excess tokens are not processed by the designated expert. GShard also proposes a random routing mechanism that selects a secondary expert with a probability proportional to its weight, under the intuition that the contribution of a secondary expert can be negligible, given that the output is a weighted average and the secondary weight is typically small. For the task of image classification with Vision Transformer (ViT) models, Riquelme et al. [8] enhance the top-k gating strategy with Batch Prioritized Routing (BPR), which assigns priority based on higher gating scores rather than the sequence order of tokens. Zoph et al. [37] have demonstrated the efficacy of BPR in the context of MoE language models. Kim et al. [76] suggest randomizing token prioritization within sequences to mitigate routing bias towards early-positioned tokens. OpenMoE [38] provides a comprehensive analysis of gating mechanisms, highlighting the “Drop-towards-theEnd” phenomenon whereby tokens later in a sequence are at greater risk of being dropped due to experts reaching their maximum capacity limits, an issue that is exacerbated in instruction-tuning datasets. Moreover, OpenMoE identifies a tendency within MoE systems to route tokens based on token-level semantic similarities, leading to “Contextindependent Specialization”. Additionally, this token ID routing specialization is established early in pretraining and remains largely fixed, resulting in a consistent pattern of token processing by the same experts throughout training, a phenomenon referred to as “Early Routing Learning”.

专家容量与令牌选择门控

在通过辅助损失实现负载均衡的基础上，GShard引入了专家容量限制机制，即设定单个专家可处理的令牌数量上限。这可能导致令牌溢出现象——超出容量的令牌将不被指定专家处理。GShard还提出随机路由机制：当主专家容量不足时，以权重比例为概率选择次优专家处理溢出令牌。由于输出为加权平均且次优权重通常较小，次优专家的贡献可忽略。针对视觉Transformer（ViT）模型的图像分类任务，Riquelme等人提出批次优先级路由（BPR）改进top-k门控策略：依据门控分数（而非令牌序列顺序）分配处理优先级。Zoph等人验证了BPR在MoE语言模型中的有效性。Kim等人建议在序列内随机化令牌优先级以缓解路由对序列前部令牌的偏好。OpenMoE系统性分析了门控机制，揭示了尾部令牌丢弃现象：由于专家容量限制，序列尾部令牌更易被丢弃，这一现象在指令微调数据集中尤为显著。此外，OpenMoE发现MoE系统倾向于基于令牌级语义相似性进行路由，导致上下文无关的专家特化；同时，这种基于令牌ID的专家特化在预训练初期即形成且高度固化，形成贯穿训练过程的早期路由学习现象。

Other Advancements on Token-Choice Gating.

Despite the implementation of gating heuristics and auxiliary expert-balancing loss functions aimed at achieving a balanced workload distribution among experts, the issue of load imbalance persists as a prevalent challenge within MoE architectures. To solve it, the Balanced Assignment of Sparse Experts (BASE) layer, as conceptualized by Lewis et al. [74] and illustrated in Figure 4 (b), re-envisions the token-to-expert allocation process by casting it as a linear assignment problem, aiming to maximize the token-expert affinities under the constraints that each expert is assigned an equal quantity of tokens. Subsequently, Clark et al. [65] introduce a variant of the BASE layer, termed S-BASE, using an optimal transport formulation. Additionally, they devise a reinforcement learning based gating algorithm employing top-1 routing, with the reward function defined as the negative cross-entropy of the predicted token. The discrete optimization of gating function can lead to convergence and statistical performance issues when training with gradientbased methods. To address these issues, Hazimeh et al. [75] introduce DSelect-k, which is a smooth version of the top-k gating algorithm that improves over standard top-k gating. This method constitutes a refined version of the top-k gating algorithm, featuring enhanced smoothness properties that yield improvements over the conventional top-k gating approach. Kudugunta et al. [77] diverge from the prevalent token-level gating strategies by introducing a sentence-level gating mechanism. This approach involves generating a sentence representation by averaging the tokens within a sequence and subsequently routing it to an expert. Chi et al. [80] observe that prevailing gating mechanisms tend to push hidden representations clustering around expert centroids, implying a trend toward representation collapse, which in turn harms model performance. To counteract this issue, they project hidden vectors into a lower-dimensional space before gating and implement L2 normalization for both token representations and expert embeddings, thus calculating gating scores within a low-dimensional hypersphere. Cai et al. [88] identify the difficulty in training the adaptive routers due to gradient vanishing, and introduce a novel strategy involving the training of a Surrogate Model (SM) that predicts LLM’s language loss given only router choices. Once trained, the SM is frozen, and the router is subsequently tuned to minimize language loss, relying exclusively on feedback from the SM. SkyworkMoE [67] proposes two innovative techniques: gating logit normalization, which improves expert diversification, and adaptive auxiliary loss coefficients, which provides layerspecific adjustment of auxiliary loss coefficients. Yuan 2.0- M32 [84] proposes a new router network, Attention Router (as illustrated in Figure 4 (e)), which implements a more efficient selection of experts and yields an enhancement in model accuracy over classical linear router network. Zeng et al. [85] posit that the complexity of token feature abstraction may necessitate a variable number of experts to process. In response, they propose AdaMoE, a novel approach that enables token-adaptive gating for MoE, allowing for a dynamic number of selected experts per token. AdaMoE subtly modifies the standard top-k MoE by incorporating a predetermined set of null experts and increasing the value of k. Importantly, AdaMoE does not mandate a uniform allocation of null experts across tokens but ensures the average engagement of null experts with a load-balancing loss, resulting in an adaptive number of null/true experts used by each token. Dynamic Mixture of Experts (DYNMoE) [87] also introduces an innovative gating mechanism that enables individual tokens to automatically determine the number of activated experts via the trainable per-expert thresholds, incorporating an adaptive process that automatically add or remove experts during training. Shi et al. [86] introduce Self-Contrast Mixtureof-Experts (SCMoE), a training-free strategy that utilizes the contrastive information among different gating strategies to engage unchosen experts during inference.

令牌选择门控的其他进展

尽管通过启发式门控与专家均衡损失试图实现负载均衡，专家间负载不均衡仍是MoE架构的核心挑战。

Lewis等人提出的稀疏专家均衡分配层（BASE）（如图4(b)）将令牌-专家分配重构为线性规划问题，在专家均衡分配约束下最大化令牌-专家亲和度。Clark等人进一步提出S-BASE变体，采用最优传输理论建模该问题，并设计基于强化学习的top-1门控算法，其奖励函数定义为预测令牌的负交叉熵。

传统门控函数的离散优化可能导致基于梯度训练的收敛性与统计性能问题，Hazimeh等人提出的DSelect-k通过平滑化top-k门控算法缓解此问题。Kudugunta等人突破令牌级路由范式，提出句子级门控机制：通过平均序列内令牌生成句子表征，再路由至专家。Chi等人发现传统门控机制易使隐表示向专家质心聚集，导致表示坍缩损害模型性能，为此提出对隐表示进行降维投影与L2归一化，在低维超球面计算门控分数。Cai等人针对自适应路由器的梯度消失问题，提出代理模型（SM）策略：先训练SM预测仅基于路由选择的语言损失，再冻结SM并基于其反馈优化路由器。SkyworkMoE创新性提出门控对数归一化（增强专家多样性）与自适应辅助损失系数（分层调节损失权重）。Yuan 2.0-M32设计注意力路由器（如图4(e)），通过更高效的专家选择提升模型精度。Zeng等人提出的AdaMoE允许令牌自适应选择专家数量：通过预置空置专家并增大k值，结合负载均衡损失实现空置/真实专家的动态配比。动态专家混合（DYNMoE）通过可训练的专家激活阈值使令牌自主决定激活专家数量。Shi等人提出自对比混合专家（SCMoE），利用不同门控策略的对比信息在推理阶段激活未选专家。

Non-trainable Token-Choice Gating.

The dynamic training of gating functions within MoE models is standard practice; however, some research has ventured into the realm of non-trainable token-choice gating mechanisms. The most significant benefit of non-trainable token-choice gating is that no additional gating network parameters are required and the full load balancing can be achieved through specific gating mechanisms. The Hash Layer [89] utilizes a random fixed gating approach by hashing the input token, achieving competitive results without the necessity of training the gating network. The load balancing is facilitated by the selection of hash functions prior to training, which can equitably distribute token batches. Zuo et al. [90] introduces THOR, an algorithm that randomly allocates two experts to each input during training and inference with a consistency regularized loss promoting consistent predictions. Gururangan et al. [91] propose the DEMix model, which explicitly assigns distinct experts to discrete pretraining domains, with domain matching being employed to select experts corresponding to the training inputs. Given the potential suboptimality of domain categorization and its limited scope in encompassing test-time domains, a single domain expert selection could undermine the model’s generalizability. To address this, DEMix adopts a parameter-free probabilistic method that dynamically estimates the domain-weighted mixture at inference. Kudugunta et al. [77] explore tasklevel gating incorporating prior knowledge tags, and similarly, M2M-100 model [92] utilizes explicit language-specific sublayers with deterministically routing input tokens based on their language. Building upon the aforementioned nontrainable gating strategies—random gating and domain mapping—PanGu-P [93] presents the Random Routed Experts (RRE) mechanism. As illustrated in Figure 4 (c), this approach initially routes tokens to a domain-specific expert group, followed by a random selection within that group.

In contrast to explicit language-specific expert selection, NLLB [78] leverages trainable gating to manage multilingual machine translation tasks, outperforming the M2M100 approach [92]. Addressing task interference in generalist models, Zhu et al. [81] introduce the Conditional MoE, which augments MoE with trainable gating by integrating conditional information at various levels, such as token-level, context-level, modality-level, task-level, and predefined token attributes. Ye et al. [79] further investigate the incorporation of trainable gating at task-level MoE. Additionally, STABLEMOE [72] identifies a challenge with existing learning-to-route MoE methods: the phenomenon of gating fluctuation. To counter this, STABLEMOE employs a two-stage training process. The first stage focuses on acquiring a balanced and cohesive gating strategy, which is then distilled into a lightweight gate function, decoupled from the backbone model. Subsequently, the second stage leverages the distilled gate for token-to-expert assignments and freezes it to ensure a stable gating strategy throughout further training.

非可训练令牌选择门控

尽管MoE模型通常动态训练门控函数，但部分研究探索了非可训练令牌选择门控机制。此类机制的核心优势在于无需额外门控网络参数，且可通过特定路由策略实现完全负载均衡。哈希层采用随机固定路由策略：对输入令牌哈希运算后直接分配专家，在无需训练门控网络的情况下取得竞争性效果。其负载均衡通过预训练阶段的哈希函数选择实现，确保令牌批次的均衡分布。Zuo等人提出THOR算法，在训练和推理阶段为每个输入随机分配两名专家，并通过一致性正则化损失促进预测一致性。Gururangan等人提出DEMix模型，将专家显式分配给离散预训练领域，基于领域匹配选择专家。鉴于领域分类可能存在次优性且覆盖测试领域有限，单一领域选择可能损害模型泛化性，DEMix采用无参数概率方法在推理时动态估计领域加权混合。Kudugunta等人探索基于先验知识标签的任务级路由，M2M-100模型则采用显式语言专用子层，根据输入语言确定性路由。基于随机路由与领域映射策略，PanGu-Π提出随机路由专家（RRE）机制（如图4(c)），先路由至领域专家组再组内随机选择。

相较于显式语言专用专家选择机制，NLLB采用可训练门控处理多语言机器翻译任务，效果优于M2M-100方案。针对通用模型的任务干扰问题，Zhu等人提出条件MoE，通过集成令牌级、上下文级、模态级等多层次条件信息增强门控可训练性。Ye等人进一步探索任务级MoE的可训练门控。STABLEMOE发现现有路由学习存在门控波动现象，提出两阶段训练：首阶段学习均衡紧凑的门控策略并蒸馏为轻量级门控函数，次阶段冻结该门控函数以保证路由稳定性。

Expert-Choice Gating.

Zhou et al. [94] propose an inversion of the conventional token-choice gating paradigm, wherein each expert selects the top-k tokens they will process, as illustrated in Figure 4 (d). This approach circumvents the necessity for auxiliary load balancing losses during training, ensuring a uniform distribution of tokens across experts. However, this method may result in uneven token coverage, with some tokens potentially being processed by multiple experts or not at all. Despite this, the technique demonstrates strong empirical performance and offers an adaptive computational interpretation where the model can implicitly apply more computation to certain tokens. The effectiveness of expert-choice gating is further validated by Zhou et al. in their subsequent Brainformers study [95]. Additionally, Komatsuzaki et al. [49] integrate the expert-choice gating strategy within the Vision Transformer and adapt it for the encoder in T5 models, while maintaining token-choice gating for the T5 decoder.

专家选择门控

Zhou等人颠覆传统令牌选择范式，提出专家选择门控（如图4(d)）：每个专家自主选择其处理的top-k令牌。该方法无需辅助负载均衡损失即可确保专家间的令牌均匀分布，但可能导致令牌覆盖不均——部分令牌被多个专家处理或完全未被处理。尽管如此，该方法展现出优越的实证性能，并为模型提供隐式计算分配能力（重要令牌可被更多专家处理）。后续研究Brainformers进一步验证其有效性。Komatsuzaki等人将该策略适配于视觉Transformer和T5编码器，同时保留T5解码器的令牌选择门控。

4.1.2 Dense

In Section 2.1, we discuss the enduring relevance of dense MoE, which activates all the experts for each input process. This dense paradigm continues to inform current innovations in MoE training and inference methodologies, as elaborated in Section 4.4.1. While sparse activation of experts, as a trade-off, may yield computational efficiency gains at the expense of some performance loss when compared to a densely activated MoE with an equivalent number of total parameters [64], [69], [73], it represents a strategic adjustment to balance computational demands with model capability. Notably, dense activation performs well in the context of LoRA-MoE fine-tuning, where the computational overhead of LoRA experts is comparatively low. This approach enables the effective and flexible integration of multiple LoRAs across a variety of downstream tasks. It preserves the generative capabilities of the original pretrained model and maintains the unique characteristics of individual LoRAs for each task [45], [63].

4.1.2 稠密门控

如第2.1节所述，稠密MoE（激活所有专家处理每个输入）仍具有持续的研究价值，其方法论创新详见第4.4.1节。尽管稀疏激活机制通过专家数量与计算效率的权衡（相比参数总量相同的稠密MoE）可能牺牲部分性能以换取效率提升，但此类策略本质上是计算需求与模型能力的动态平衡。值得注意的是，在LoRA-MoE微调场景中，稠密激活表现优异：由于LoRA专家的计算开销较低，该方法能灵活集成多任务LoRA适配器，既保留预训练模型的生成能力，又维持各任务LoRA特性。

4.1.3 Soft

Deciding the allocation of appropriate experts to each input token pose the fundamental discrete optimization challenge for sparse MoE. This often necessitates heuristic auxiliary losses to ensure balanced expert engagement and to minimize unassigned tokens. These issues become more pronounced in scenarios involving out-of-distribution data, such as small inference batches, novel inputs, or during transfer learning. Similar to dense MoE, the soft MoE approach maintains full differentiability by leveraging all the experts for processing each input, thus avoiding issues inherent to discrete expert selection. We distinguish soft MoE from dense MoE to highlight the characteristic that mitigates computational demands through the gating-weighted merging of input tokens or experts.

4.1.3 软性门控

稀疏MoE中令牌-专家的离散分配本质上面临组合优化挑战，通常依赖启发式辅助损失确保专家均衡参与并最小化未分配令牌。这些问题在分布外数据（如小批量推理、新输入或迁移学习）中更为显著。与稠密MoE类似，软性MoE通过全专家参与处理输入实现完全可微分性，避免离散选择问题。其与稠密MoE的核心区别在于：通过输入令牌或专家的门控加权融合降低计算需求。

Token Merging.

Puigcerver et al. [39] proposed the Soft MoE, which eschews the conventional sparse and discrete gating mechanism in favor of a soft assignment strategy that merges tokens. This method computes several weighted averages of all tokens, with weights depending on both tokens and experts, and processes each aggregate with its respective expert. Their experimental results in image classification demonstrate that soft MoE enhances the stability of gating function training and inherently maintains balance. HOMOE [96] follows the design of Soft MoE and combines it with Hopfield network to address the the challenges of Compositional Zero-Shot Learning tasks. Yet, merging input tokens complicates its application in auto-regressive decoders, as future tokens required for averaging are inaccessible during inference.

令牌融合

Puigcerver等人提出Soft MoE，摒弃传统离散门控机制，通过令牌加权平均实现软分配：基于令牌与专家的双重权重计算加权聚合表征，再由各专家处理聚合结果。图像分类实验表明，该方法提升门控训练稳定性且天然保持均衡。HOMOE结合Soft MoE与Hopfield网络，解决组合零样本学习任务难题。但令牌融合因需要未来令牌参与平均，难以适配自回归解码场景。

Expert Merging.

In contrast to the merging of input tokens, Muqeeth et al. [40] introduced the Soft Merging of Experts with Adaptive Routing (SMEAR) framework, which circumvents discrete gating by merging all the experts’ parameters through a weighted average, as illustrated in Figure 4 (f). They argue that conventional sparse MoE models often fail to match the performance of their parameter-matched dense counterparts or those utilizing non-learned heuristic gating functions, potentially due to flawed gradient estimation methods for training modules with non-differentiable, discrete gating decisions. By processing the input tokens through a single merged expert, SMEAR does not incur a significant increase in computational costs and enables standard gradient-based training. Empirical evaluations on T5-GLUE and ResNet-DomainNet benchmarks reveal that SMEAR-equipped models surpass those with metadata-based [77], [91] or gradient-estimated learning gating strategies. On ResNet-DomainNet, SMEAR achieved a 1.5% higher average accuracy than Soft MoE [39] with single “slot” per expert, at the expense of a near 10% reduction in throughput. Subsequent contributions by Zhong et al. [41] argue that SMEAR’s demonstrated advantages are confined to downstream fine-tuning on classification tasks. They present Lory, an innovative approach for scaling such expert merging architectures to auto-regressive language model pretraining. Lory [41] introduces a causal segment routing strategy, conducting expert merging at the segment level while maintaining the auto-regressive nature of language models. Furthermore, it employs similaritybased data batching to direct expert specialization in particular domains or topics. Lory’s empirical validation on LLaMA models showcases significant improvements over parameter-matched dense models in terms of perplexity (by 13.9%) and on diverse downstream tasks (by 1.5%-11.1%), highlighting the potential of fully-differentiable MoE architectures for language model pretraining and encouraging further investigation in this area.

In addition, expert merging methods have demonstrated efficacy in parameterefficient fine-tuning (PEFT) MoE contexts. Zadouri et al. [42] substantiate that soft merging of experts significantly outperforms sparse gating mechanisms (top-1, top-2) in the T5 models [171] fine-tuning with the MoV-10 setting of 10 (IA)3 vector expert. Wu et al. [43] propose Omni-SMoLA, an architecture leveraging the soft method to mix multimodal low-rank experts, improving the generalist performance across a broad range of generative vision-language tasks. He et al. [97] introduce Merging Experts into One (MEO), merging multiple selected experts into one to reduce the expert computation cost. Moreover, they perform the expert selection at the sequence level and employ a token attention mechanism for capturing the identification of each token, thus preserving context information without the necessity of merging distinct weights and biases for individual tokens.

专家融合

Muqeeth等人提出自适应路由专家软合并框架（SMEAR）（如图4(f)），通过专家参数的加权平均规避离散门控。研究表明，传统稀疏MoE因不可微门控的梯度估计缺陷，性能常不及参数匹配的稠密模型或启发式门控方法。SMEAR以单融合专家处理输入，计算开销增幅可控且支持标准梯度训练。在T5-GLUE与ResNet-DomainNet基准测试中，SMEAR超越基于元数据或梯度估计门控的模型，其中ResNet-DomainNet上以10%吞吐量代价实现1.5%平均精度提升。Zhong等人指出SMEAR优势限于分类任务微调，提出面向自回归预训练的Lory框架：采用因果段路由策略（段级专家融合保持自回归性），结合相似性数据批处理引导专家领域特化。LLaMA模型验证显示，Lory相比参数匹配稠密模型，困惑度降低13.9%，多任务性能提升1.5%-11.1%，彰显全可微MoE架构的预训练潜力。

延伸应用
专家融合在高效参数微调（PEFT）场景同样有效：Zadouri等人验证T5模型在MoV-10设置下，专家软合并显著优于稀疏门控（top-1/2）；Wu等人提出Omni-SMoLA，通过多模态低秩专家软融合提升视觉-语言生成任务性能；He等人提出MEO框架，将多专家合并为单一专家以降低计算成本，并通过序列级专家选择与令牌注意力机制保留上下文信息。

4.2 Experts

In this section, we delineate the architecture of expert networks within MoE framework, following our discussion on the gating function that orchestrates the activation of these experts.

本节基于前文所述的门控函数设计，深入解析MoE框架中专家网络的架构特性。

4.2.1 Network

Types Since the initial integration of MoE into transformer architectures [28], [36], [37], MoE has served as a substitute for Feed-Forward Network (FFN) modules within these models. Typically, each expert within a MoE layer replicates the architecture of the FFN it replaces. This paradigm, wherein FFNs are utilized as experts, remains predominant, and subsequent refinements will be expounded upon in Sections 4.2.2 to 4.2.4.

4.2.1 网络类型

自MoE首次融入Transformer架构以来，其核心应用场景始终聚焦于替代模型中的前馈网络（FFN）模块。典型设计中，MoE层的每个专家均复刻原FFN结构。以FFN作为专家网络的范式至今仍为主导，其优化路径将在4.2.2至4.2.4节展开。

Feed-Forward Network.

As discussed in existing work [54], the predilection for leveraging MoE in the context of FFNs is rooted in the hypothesis that self-attention layers exhibit lower sparsity and less domain specificity than FFN layers. Pan et al. [64] provide empirical support for this, revealing marked sparsity in FFN layers compared to self-attention layers, through their analysis of downstream Wikitext tasks using their pretrained DS-MoE models. Their results indicate a mere 20% active expert engagement in FFN layers, in contrast to the 80% observed within selfattention layers. In earlier investigation of FFN computational patterns, Zhang et al. [50] and Li et al. [172] observe that most inputs only activate a small proportion of neurons of FFNs, highlighting the inherent sparsity of FFNs. Subsequently, Zhang et al. [98] observe the Emergent Modularity (EM) phenomenon within pretrained Transformers, revealing a significant correlation between neuron activation and specific tasks (evidenced by the functional specialization of neurons and function-based neuron grouping). This discovery supports the proposition that the MoE structure reflects the modularity of pre-trained Transformers.

前馈网络

现有研究指出，MoE优先适配FFN层源于其相比自注意力层具有更高稀疏性与领域特异性。Pan等人通过DS-MoE模型在Wikitext任务的实证分析验证：FFN层专家激活率仅20%，显著低于自注意力层的80%。早期对FFN计算模式的探索发现，多数输入仅激活少量FFN神经元，揭示了FFN的固有稀疏性。Zhang等人进一步观察到预训练Transformer中的涌现模块化（EM）现象：神经元激活与特定任务强相关（体现为神经元功能特化与任务导向的神经元聚类），这为"MoE结构反映预训练模型模块化本质"提供了理论支撑。

Attention.

While the focus of MoE research has predominantly been on FFN layers within the Transformer architecture, Zhang et al. [82] introduce the Mixture of Attention Heads (MoA), an innovative architecture that combines multi-head attention layers with MoE to further enhance performance and restrain computational cost. As delineated in Figure 5 (a), MoA employs two sets of experts, one for query projection and one for output projection. Both sets select the experts with the same indices through a common gating network. To reduce computational complexity, MoA shares the key (Wk) and value (Wv) projection weights across attention experts, with experts differentiated only by their respective query (qtW q i ) and output (oi,tWo i ) projection weights, allowing for shared pre-computation of key (KWk) and value (V Wv) sequences. Subsequent work such as DSMoE [64], JetMoE [83], and ModuleFormer [73] follows the design of MoA and further refines the combination of MoE and attention layer.

注意力机制

在主流研究聚焦FFN-MoE的背景下，Zhang等人提出注意力头混合（MoA）架构（如图5(a)），通过将MoE融入多头注意力层实现性能突破与计算约束。MoA设置两类专家：查询投影专家与输出投影专家，共享门控网络确保两组专家索引同步选择。为降低计算复杂度，MoA在注意力专家间共享键（Wk）与值（Wv）投影权重，仅通过差异化的查询（qtW q_i）与输出（oi,tWo_i）投影实现专家分化，支持键（KWk）与值（V Wv）序列的预计算优化。后续DSMoE、JetMoE、ModuleFormer等研究均沿袭MoA设计理念，持续完善MoE与注意力层的融合机制。

Others.

In addition to the aforementioned expert network types, researchers have explored the use of Convolutional Neural Network (CNN) as expert [99], [100], [101], [102], [173]. Moreover, recent endeavors that integrate Parameter-Efficient Fine-Tuning (PEFT) techniques with MoE, such as employing Low-Rank Adaptation (LoRA) [174] as expert, have shown promising results, which are discussed in Section 4.3.

其他类型

除上述类型外，学者探索了卷积神经网络（CNN）作为专家网络的可行性。近期研究将参数高效微调（PEFT）技术融入MoE框架（如采用低秩适应LoRA作为专家），展现出显著效果，具体进展详见4.3节。

4.2.2 Hyperparameters

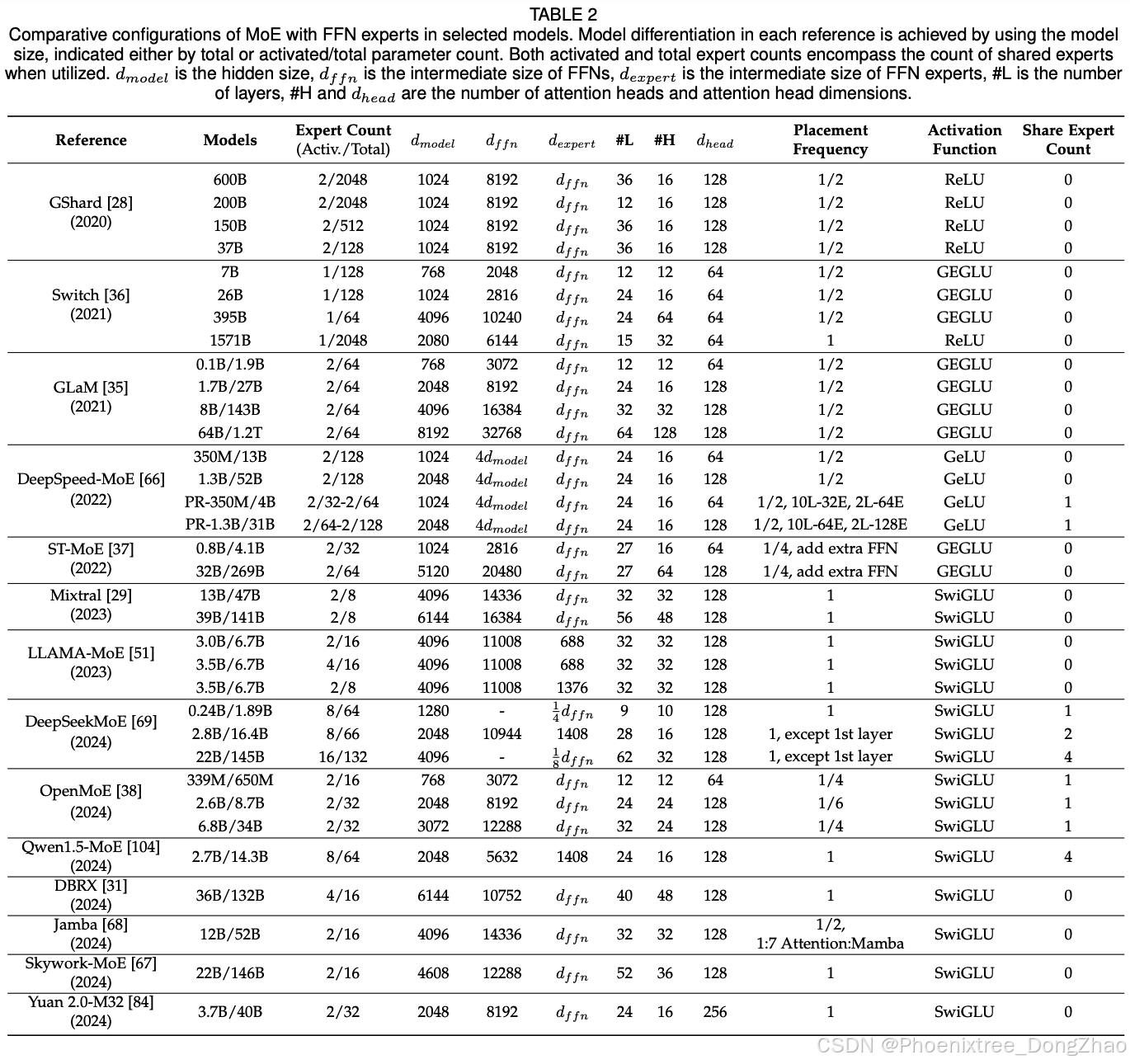
The scale of sparse MoE models is governed by several critical hyperparameters that extend beyond those of dense transformer models. These include (1) the count of experts per MoE layer, (2) the size of each expert, and (3) the placement frequency of MoE layers throughout the model. The selection of these hyperparameters is crucial, as it profoundly influences model performance and computational efficiency across various tasks. Optimal hyperparameter choices are thus contingent upon the specific application requirements and the constraints of the computational infrastructure. Our subsequent analysis, informed by the exemplified models listed in Table 2, explores these hyperparameter decisions in depth. Meanwhile, we enumerate some recent open-source models, summarizing their number of parameters and benchmark performance in Table 3.

4.2.2 超参数

稀疏MoE模型的规模由若干关键超参数决定，其配置策略显著区别于稠密Transformer模型。核心超参数包括：(1) 每层专家数量，(2) 专家规模，(3) MoE层部署频率。这些参数的选择深刻影响模型性能与计算效率，需根据具体任务需求与算力约束动态优化。基于表2的典型模型分析，本节深入探讨超参数配置策略，表3进一步汇总近期开源模型的参数量与基准表现。

Expert Count.

Initial investigations employing thousands of experts per layer yielded impressive gains in pretraining and translation quality [27], [28], [36]. Nonetheless, the quality of sparse MoE models is disproportionately reduced under domain shift [103] or when fine-tuning on diverse task distributions [36]. GLaM [35] adopts a configuration of 64 experts, guided by their findings that a 64- expert setup with top-2 gating strikes an optimal balance between execution efficiency and performance across zeroshot, one-shot, and few-shot scenarios. Reflecting this trend, more recent sparse MoE models [29], [31], [37], [38], [67], [68], [84], [104] commonly utilize no more than 64 experts. Additionally, DeepSpeed-MoE [66] adopts a Pyramid-MoE approach, positioning MoE layers with a larger expert count towards the network’s end.

专家数量

早期研究通过单层部署数千名专家显著提升预训练与翻译质量，但面临领域迁移与多任务微调的性能衰减问题。GLaM模型基于实验提出64专家+top-2门控配置，在零样本/单样本/少样本场景下实现效率-性能最优平衡。后续稀疏MoE模型普遍遵循该上限，DeepSpeed-MoE采用金字塔式MoE策略，在模型末端部署更高专家数量的MoE层。

Expert Size.

To scale the model effectively, GLaM [35] prioritizes the expansion of the intermediate hidden dimension per expert while standardizing the expert count at 64, a strategy that often requires the implementation of tensor parallelism across multiple accelerators to maintain computational efficiency [35], [36], [66]. From this period forward, MoE models [29], [31], [37], [67] typically featured larger expert dimensions. Differently, DeepSeekMoE [33], [69] introduces the concept of fine-grained expert segmentation by subdividing the intermediate hidden dimension of FFN expert, while preserving the overall parameter count. Specifically, DeepSeekMoE-145B employs a reduced intermediate hidden dimension at one-eighth that of its dense FFN counterpart, increasing both the number of experts (from 16 to 128) and the number of active experts (from top-2 to top16) by a factor of eight. They believe that this strategy not only refines the decomposition of knowledge across experts, facilitating more precise learning, but also enhances the flexibility of expert activation combinations, allowing for more specialized and targeted knowledge capture. Qwen1.5-MoE [104] and DBRX [31] adopt a similar fine-grained expert segmentation strategy. Results from LLAMA-MoE [51], which allocates dense FFN parameters across non-overlapping experts to maintain a consistent parameter count, indicate that activating 4 out of 16 experts with a dimensionality of dexpert = 688 marginally outperforms the activation of 2 out of 8 experts with dexpert = 1376. Furthermore, Parameter Efficient Expert Retrieval (PEER) [105], an innovative layer design employing the product key technique [175] for sparse retrieval from a vast pool of tiny experts (over a million single-neuron experts), surpasses dense FFNs and coarsegrained MoEs in terms of performance-compute trade-off on language modeling tasks.

专家规模

GLaM通过扩大专家中间隐藏维度（固定64专家数量）实现模型扩展，该策略需配合跨加速器的张量并行技术[35][36][66]。此后主流模型[29][31][37][67]普遍采用大维度专家设计。DeepSeekMoE创新性提出细粒度专家划分策略：将FFN专家的中间维度拆分为多份（总参数量不变），如DeepSeekMoE-145B将中间维度压缩至稠密FFN的1/8，专家数量与激活数均扩大8倍（16→128专家，top-2→top-16）。该设计强化知识解耦精度与专家组合灵活性，Qwen1.5-MoE与DBRX均采用类似方案。LLAMA-MoE实验表明：16专家中激活4个（维度688）优于8专家中激活2个（维度1376）。PEER通过百万级单神经元专家池+稀疏检索技术，在语言建模任务中实现优于稠密FFN与粗粒度MoE的性价比。

Frequency of MoE Layers.

Sparse MoE models typically evolve from dense architectures by interspersing MoE layers in place of the dense FFN layers at regular intervals. Although a higher frequency of MoE layers can enlarge the model size, it also introduces greater system overhead. In practice, most MoE models features alternate FFN replacement (1/2) with MoE layers [28], [35], [66], [103]. Nevertheless, variations exist, with some models incorporating MoE layers every fourth layer (1/4) [37], [38] or in every layer (1/1) [36], [69]. Following the introduction of Mixtral 8x7B [29], the trend seems to shift towards placing MoE in every layer of the model, with a common choice of only 8 or 16 experts mirroring the dimensionality of a dense FFN [31], [67], [69], [104].

Research into the optimal configuration of MoE layers has been extensive. V-MoE [8] employs MoE in the last few even-numbered Transformer layers, noting that, despite using fewer MoE layers, the impact on performance is minimal while computational speed is significantly enhanced. DeepSeekMoE-16B/-145B [69] replaces all FFNs with MoE layers, excluding the first, due to the observed slower convergence of load balance status in the first layer. MoE-LLaVA [106], a recently popular open Large VisionLanguage Model (LVLM), demonstrates that alternating MoE placement yields superior model quality and execution efficiency on multimodal tasks, compared to everylayer MoE placement or ”First-Half” and ”Second-Half” configurations. ST-MoE [37] found that adding a dense FFN adjacent to each MoE layer can improve model quality. Brainformers [95] introduce a nonuniform architecture that integrates MoE layers, dense FFNs, attention mechanisms, and a variety of layer normalizations and activation functions without strict sequential layering, trading architectural regularity for the flexibility of sub-layer composition. Jamba [68] integrates the architecture of Mamba [176] by adopting a 1:7 ratio of attention-to-Mamba layers.

MoE层频率

稀疏MoE模型通常以规律间隔替换稠密FFN层。更高部署频率虽可扩展模型容量，但显著增加系统开销。主流方案包括：

间隔替换（1/2层）[28][35][66][103]
低频替换（1/4层）[37][38]
全层替换（1/1层）[36][69]

Mixtral 8x7B引领全层部署趋势，近期模型[31][67][69][104]多采用8或16专家配置以匹配稠密FFN维度。研究进展显示：

V-MoE在末段偶数层部署MoE，以较小性能损失换取显著加速
DeepSeekMoE排除首层MoE（因首层负载均衡收敛慢）
MoE-LLaVA验证交替部署在多模态任务中优于全层/半层配置
ST-MoE通过MoE层旁置稠密FFN提升模型质量
Brainformers打破层序限制，异构集成MoE/稠密FFN/注意力机制
Jamba以1:7比例混合注意力层与Mamba层

4.2.3 Activation Function

Building upon dense Transformer architectures, sparse MoE models have adopted a progression of activation functions paralleling those in leading dense large language models, including BERT [181], T5 [171], GPT [2], LLAMA [161] and so on. The evolution of activation functions has seen a shift from ReLU [107] to more advanced options such as GeLU [108], GeGLU [109], and SwiGLU [109]. This trend extends to other components of MoE models, which now frequently incorporate Root Mean Square Layer Normalization (RMSNorm) [182], Grouped Query Attention (GQA) [183], and Rotary Position Embeddings (RoPE) [184].

4.2.3 激活函数

稀疏MoE模型沿袭稠密Transformer的激活函数演进路径，从ReLU逐步升级至GeLU、GeGLU、SwiGLU等先进方案。技术生态融合趋势显著，现代MoE模型普遍集成：

RMSNorm层标准化
分组查询注意力（GQA）
旋转位置编码（RoPE）

该演进在BERT、T5、GPT、LLaMA等主流架构中均有体现，持续推动MoE组件在计算效率与表达能力上的优化。

4.2.4 Shared Expert

DeepSpeed-MoE [66] innovatively introduces the ResidualMoE architecture, wherein each token is processed by a fixed expert and another selected through gating, achieving two experts engagement per layer without increasing the communication cost beyond that of top-1 gating. This approach considers the gating-selected MoE expert as an error-correcting adjunct to the fixed dense FFN. A conceptually similar approach, Conditional MoE Routing (CMR), is employed in NLLB [78], which also combines the outputs of dense FFN and MoE layers. This paradigm of integrating fixed FFN with sparse MoE, often referred to as shared expert and illustrated in Figure 5 (b), has gained traction in recent language models such as DeepSeekMoE [69], OpenMoE [38], Qwen1.5-MoE [104], and MoCLE [46], indicating its ascension to a mainstream configuration. Instead of using a single shared expert, DeepSeekMoE [69] and Qwen1.5- MoE [104] employ multiple shared experts, due to their fine-grained expert segmentation design. He et al. [111] introduce Partially Dynamic Networks (PAD-Net), iteratively transforming partial parameters of gating-selected experts into static parameters (akin to shared experts) based on their impact on loss values. Zhao et al. [112] introduce HyperMoE, an innovative MoE framework that integrates expert-shared and layer-shared hypernetwork to effectively capture cross-expert and cross-layer information. Additionally, based on the design of shared expert, ScMoE [110] decouples the MoE process to separately handle the representations from preceding layers and integrate them with the outputs processed by the shared expert of the current layer, thus improving efficiency by facilitating overlap in communication and computation. A comparable method to enhance overlapping is employed in the Dense-MoE hybrid transformer architecture, as delineated in Snowflake Arctic [32], which bears resemblance to the LoRA MoE framework discussed in Section 4.3.3 and illustrated in Figure 6 (d).

4.2.4 共享专家

DeepSpeed-MoE[66]创新性提出残差MoE架构（ResidualMoE），通过固定专家+门控专家的双路处理模式（如图5(b)），在保持top-1门控通信成本的前提下实现每层双专家协作。其核心思想是将门控选择的MoE专家视为固定稠密FFN的误差修正模块。类似地，NLLB采用条件式MoE路由（CMR），融合稠密FFN与MoE层输出。这种"固定FFN+稀疏MoE"的共享专家范式已在DeepSeekMoE、OpenMoE、Qwen1.5-MoE、MoCLE等最新语言模型中广泛应用，成为主流配置方案。DeepSeekMoE与Qwen1.5-MoE基于细粒度专家划分设计，采用多共享专家架构替代单一共享专家。He等人提出部分动态网络（PAD-Net），根据专家对损失值的影响度，逐步将门控选择专家的部分参数固化为类共享专家。Zhao等人的HyperMoE框架通过专家共享+层级共享的超网络捕获跨专家/跨层信息。ScMoE在共享专家基础上解耦MoE流程，将前置层表征与当前层共享专家输出异步集成，通过通信-计算重叠提升效率。Snowflake Arctic的稠密-MoE混合架构（类似4.3.3节LoRA MoE）也采用类似重叠优化策略。

4.3 Mixture of Parameter-Efficient Experts

LLMs pretrained on generic massive datasets have demonstrated impressive abilities, enabling their deployment across diverse tasks [118]. However, to tailor a pretrained LLM for a specific downstream task, fine-tuning is essential. Traditional full fine-tuning, which updates all the parameters of the base model, is computationally intensive, especially as model sizes continue to grow [185]. To address this issue, research into parameter-efficient fine-tuning (PEFT) has emerged, intending to reduce computational demands during the adaptation of a generic pretrained model to particular tasks [186]. PEFT methods only update a small set of parameters while maintaining the rest of the base model untouched [187]. As an example of PEFT, LoRA [174] introduces two low-rank matrices to receive incremental updates associated with the task-specific fine-tuning. Only the LoRA matrices are updated while the base model is kept untouched during fine-tuning. These techniques have achieved state-of-the-art performance across numerous NLP tasks [174], [188].

Despite these successes, PEFT approaches often struggle with generalizing across multiple tasks due to their limited scope of trainable parameters and the potential for catastrophic forgetting [114]. To mitigate these limitations, a line of mixture of parameter-efficient experts (MoPE) research has emerged, focusing on integrating the MoE framework with PEFT [114], [119]. MoPE incorporates the MoE’s gating mechanism and multi-expert architecture, but with each expert constructed using PEFT techniques [189]. The subtle combination boosts PEFT’s performance under the multi-task scenario [116]. Additionally, by leveraging PEFT for constructing experts, MoPE operates with fewer parameters, achieving greater resource efficiency compared to traditional MoE models [42].

MoPE harnesses the best of both fields: the task versatility of MoE and the resource efficiency of PEFT [114], positioning it as a promising area of study that pushes the boundaries of both fields. In the following subsection, we will give a taxonomy of MoPE, as depicted in Figure 6, based on their placement within the Transformer model architecture. We will then review recent MoPE research, summarizing the methodologies and contributions.

4.3 参数高效专家混合

在通用大规模数据集上预训练的大语言模型（LLMs）展示了令人印象深刻的能力，使其能够部署在各种任务中。然而，为了使预训练的LLM适应特定的下游任务，微调是必不可少的。传统的全参数微调会更新基础模型的所有参数，计算成本高昂，尤其是随着模型规模的不断增长。为了解决这个问题，参数高效微调（PEFT）研究应运而生，旨在减少将通用预训练模型适配到特定任务时的计算需求。PEFT方法仅更新一小部分参数，同时保持基础模型的其余部分不变。以LoRA为例，它引入了两个低秩矩阵来接收与任务特定微调相关的增量更新。在微调过程中，仅更新LoRA矩阵，而基础模型保持不变。这些技术在众多NLP任务中实现了最先进的性能。

尽管取得了这些成功，PEFT方法在多任务泛化方面往往表现不佳，原因是其可训练参数范围有限以及可能出现的灾难性遗忘问题。为了缓解这些限制，参数高效专家混合（MoPE）研究逐渐兴起，专注于将MoE框架与PEFT结合。MoPE结合了MoE的门控机制和多专家架构，但每个专家都使用PEFT技术构建。这种巧妙的结合在多任务场景下提升了PEFT的性能。此外，通过利用PEFT构建专家，MoPE以更少的参数运行，相比传统的MoE模型实现了更高的资源效率。

MoPE融合了两个领域的最佳特性：MoE的任务多样性和PEFT的资源效率，使其成为一个有前景的研究领域，推动了两者的边界。在接下来的小节中，我们将根据MoPE在Transformer模型架构中的位置，给出其分类，如图6所示。然后，我们将回顾近期的MoPE研究，总结其方法和贡献。

4.3.1 Feed-Forward Network

Following the conventional MoE structure, a series of investigations introduce the MoPE framework to the FFN layer of every Transformer block. During the training process, the focus is on optimizing the parameter-efficient experts and the gating mechanism, leaving the rest of the pretrained model intact. As illustrated in Figure 6(b), the forward process under the MoPE framework integrated with FFN can be expressed as:

where ∆W^{ffn} and G^{ffn}(x') is the parameter-efficient expert and gating function applied to the FFN layer, respectively.

One of the pioneering studies in this domain, LoRAMoE [45], efficiently applies the MoPE structure to FFN. LoRAMoE integrates a few plug-in LoRA experts into the FFN layer, employing a gating mechanism to orchestrate the experts’ contributions. Realizing the diversity in data distributions, LoRAMoE separates the experts into two distinct groups: one focuses on learning various downstream tasks, and the other is dedicated to aligning pretrained world knowledge with human instructions. To ensure that each group of experts maintains its focus, LoRAMoE defines a localized balancing constraint loss, which preserves the importance of each expert within its group while allowing different groups to concentrate on their respective tasks. This design enables LoRAMoE to effectively resolve the knowledge forgetting issue and enhance model performance on downstream tasks. In a similar vein, AdaMix [44] injects a set of Adapter [190] experts after the FFN layer in each Transformer block. Adapter tuning is a PEFT method that integrates a pair of feed-forward up and down projection matrices into the Transformer block. During fine-tuning, only the incremental Adapter blocks are updated, with the rest of the model unchanged. AdaMix utilizes a stochastic routing policy that randomly selects the projection matrices during training, maintaining computational costs equivalent to a single adapter. To minimize service costs during inference, AdaMix averages the outputs of all the experts.

4.3.1 前馈网络

遵循传统的混合专家（MoE）架构，一系列研究将参数高效专家混合（MoPE）框架引入每个Transformer模块的前馈网络（FFN）层。在训练过程中，仅优化参数高效专家和门控机制，保持预训练模型的其余部分不变。如图6(b)所示，结合FFN的MoPE框架下的正向过程可表示为：

其中，∆W^{ffn}和G^{ffn}(x')分别为应用于FFN层的参数高效专家函数和门控函数。

该领域的开创性研究之一，LoRAMoE，高效地将MoPE结构应用于FFN。LoRAMoE在FFN层中集成了少量LoRA专家插件，通过门控机制协调专家的贡献。认识到数据分布的多样性，LoRAMoE将专家分为两组：一组专注于学习各种下游任务，另一组致力于对齐预训练的世界知识与人类指令。为了确保每组专家保持专注，LoRAMoE定义了局部平衡约束损失，保留组内专家的重要性，同时允许不同组专注于各自的任务。这一设计使LoRAMoE能够有效解决知识遗忘问题，并提升下游任务的模型性能。类似地，AdaMix在FFN层后注入了Adapter专家集合。Adapter微调是一种PEFT方法，将一对前馈上投影和下投影矩阵集成到Transformer模块中。在微调过程中，仅更新增量Adapter模块，模型的其余部分保持不变。AdaMix采用随机路由策略，在训练时随机选择投影矩阵，保持计算成本与单个Adapter相当。为了最小化推理时的服务成本，AdaMix对所有专家的输出进行平均。

Taking a different approach, MixDA [113] includes two training stages to leverage domain-specific knowledge while preserving learned information. During the first stage, MixDA only fine-tunes the domain-adapters that work in parallel with the FFN to acquire domain-specific knowledge while simultaneously retaining the world knowledge. In the second stage, MixDA introduces a gating network and taskadapters on top of the FFN layer for tailoring the model to specific downstream tasks. This strategy allows for a more nuanced adaptation to the task at hand. LLaVA-MoLE [115] extends the application of MoPE to multimodal tasks. It creates a set of LoRA experts for the FFN layer to handle inputs from different domains, enhancing the model’s versatility. LLaVA-MoLE adopts a top-1 routing strategy, activating the most relevant expert based on the router’s output distribution, thus maintaining computational costs close to a standard FFN with LoRA. This framework is effective in addressing data conflicts and consistently surpasses plainLoRA baselines across diverse data configurations.

Contrasting with the MoPE implementations we have discussed, MixLoRA [114] creates a LoRA-MoE framework that closely aligns with the conventional MoE models. Rather than just plugging in multiple lightweight experts, MixLoRA fuses LoRA experts with the shared FFN layer. By leveraging the base weights from a single FFN of the base model, MixLoRA streamlines the creation of the MoPE architecture. Furthermore, MixLoRA implements a high-throughput framework that significantly reduces token computation latency and memory usage during both training and inference, optimizing performance and efficiency.

MixDA 采取了不同的方法，包括两个训练阶段，以利用领域特定知识，同时保留已学习的信息。在第一阶段，MixDA仅微调与FFN并行工作的领域适配器，以获取领域特定知识，同时保留世界知识。在第二阶段，MixDA在FFN层上引入门控网络和任务适配器，以定制模型以适应特定下游任务。这一策略允许更细致地适应任务。LLaVA-MoLE将MoPE的应用扩展到多模态任务。它为FFN层创建了一组LoRA专家，以处理来自不同领域的输入，增强了模型的多样性。LLaVA-MoLE采用top-1路由策略，根据路由器的输出分布激活最相关的专家，从而保持计算成本接近标准的LoRA-FFN。该框架有效解决了数据冲突问题，并在多样数据配置中始终超越plainLoRA基线。

与我们讨论的MoPE实现不同，MixLoRA创建了一个与传统MoE模型高度对齐的LoRA-MoE框架。MixLoRA不是简单地插入多个轻量级专家，而是将LoRA专家与共享的FFN层融合。通过利用基础模型中的单个FFN的基权重，MixLoRA简化了MoPE架构的创建。此外，MixLoRA实现了一个高吞吐量框架，显著减少了训练和推理期间令牌计算的延迟和内存使用，优化了性能和效率。

4.3.2 Attention

A branch of research has been exploring the application of the MoPE framework with the attention mechanism. These studies typically involve augmenting the attention mechanism by incorporating a gating network and a set of parallel experts. The MoPE framework can be applied to the Query, Key, Value, and Output projection modules, individually or in various combinations, within the attention mechanism. During the fine-tuning process, only the parameters of the activated experts and the gating network are updated, while the remaining parameters of the model are kept frozen. For example, as shown in Figure 6(a), the integration of MoPE with the Key and Value module of the attention mechanism can be formalized as follows:

where Q, K, V represents the Query, Key and Value modules, respectively. ∆W^k and G^k(x) denote the parameterefficient expert and its corresponding gating function for the Key module. Similarly, ∆W^v and G^v(x) indicate the expert and the gating function for the Value module. Here, n is the number of experts, and d_head is the dimensions in the Multi-head Attention mechanism.

Recent studies have demonstrated the effectiveness of extending MoE to the attention layer [73], [82], [83]. Additionally, there is a new line of research has focused on the fusion of MoPE with the attention mechanism to enhance the model’s efficiency and adaptability. For instance, MoELoRA [47] applies MoE to the attention mechanism in a resourceefficient manner by leveraging a PEFT method, adopting LoRA [174] to construct the experts. Specifically, MoELoRA sets multiple LoRA experts to the Query and Value matrices of the attention mechanism, and utilizes a gating network to activate the top-k experts related to the specific tasks during both training and inference phases. To alleviate routing randomness, MoELoRA employs a contrastive learning loss to control the training of experts. The contrastive learning loss is designed to accentuate the differences in output distributions between experts, thereby encouraging them to capture diverse features relevant to the downstream tasks. MoELoRA offers a solution for flexibly combining various computational modules tailored to downstream tasks.

Another framework, MoCLE [46], aims to resolve task conflicts that arise from the diversity of training tasks of different sources and formats. MoCLE utilizes a clustering model to categorize different tasks and then leverages a router to direct the clustered input to LoRA experts inserted into the Query and Value modules of the attention mechanism. These LoRA experts contain a group of multiple task experts and a universal expert. Each task expert is dedicated to a particular task to reduce task conflicts, while the universal expert, trained on all tasks, helps to maintain model generalization. SiRA [116] introduces several lightweight LoRA adapters as experts, along with a top-k gating mechanism. To mitigate load imbalance and over-fitting issues, SiRA incorporates a capacity constraint that limits the number of tokens each expert can process. Additionally, it employs an auxiliary loss to promote load balancing and an expert dropout mechanism to equalize the gating distribution. SiRA provides an efficient and finegrained approach to improving the quality of LoRA.

4.3.2 注意力机制

一系列研究探索了将MoPE框架应用于注意力机制。这些研究通常通过引入门控网络和一组并行专家来增强注意力机制。MoPE框架可以单独或以各种组合方式应用于注意力机制中的Query、Key、Value和Output投影模块。在微调过程中，仅更新激活专家和门控网络的参数，模型的其余参数保持冻结。例如，如图6(a)所示，MoPE与注意机制的Key and Value模块的集成可以形式化如下：

其中Q， K， V分别代表Query， Key和Value模块。∆W^k和G^k(x)表示Key模块的参数高效专家及其对应的门控函数。同样，∆W^v和G^v(x)表示专家和Value模块的门控函数。这里，n是专家的数量，d_head是多头注意机制的维度。

最近的研究证明了将MoE扩展到注意力层的有效性。此外，新的研究方向集中在将MoPE与注意力机制融合，以增强模型的效率和适应性。例如，MoELoRA 以资源高效的方式将MoE应用于注意力机制，采用LoRA 构建专家。具体来说，MoELoRA在注意力机制的Query和Value矩阵中设置了多个LoRA专家，并利用门控网络在训练和推理阶段激活与特定任务相关的top-k专家。为了缓解路由随机性，MoELoRA采用对比学习损失来控制专家的训练。对比学习损失旨在突出专家输出分布之间的差异，从而鼓励他们捕获与下游任务相关的多样化特征。MoELoRA提供了一种灵活组合下游任务定制化计算模块的解决方案。

另一个框架，MoCLE，旨在解决由于不同来源和格式的训练任务多样性导致的任务冲突。MoCLE利用聚类模型对任务进行分类，然后通过路由器将聚类后的输入引导到插入到注意力机制Query和Value模块中的LoRA专家。这些LoRA专家包含一组多任务专家和一个通用专家。每个任务专家专注于特定任务以减少任务冲突，而通用专家在所有任务上训练，有助于保持模型的泛化能力。SiRA引入了几个轻量级LoRA适配器作为专家，并采用top-k门控机制。为了缓解负载不平衡和过拟合问题，SiRA引入了容量约束，限制每个专家处理的令牌数量。此外，它采用辅助损失来促进负载平衡，并通过专家丢弃机制均衡门控分布。SiRA提供了一种高效且细粒度的方法来提升LoRA的质量。

4.3.3 Transformer Block

The integration of MoPE with the Transformer architecture has received substantial attention in recent research. This approach involves creating two groups of experts: one for the attention mechanism, and another for the FFN within the Transformer block. Each group is regulated by its gating mechanism to control the activation of the experts. As exhibited in Figure 6(c), the forward process under the MoPE framework integrated with the Transformer block can be denoted as:

MoV [42] is one of the notable attempts that combine MoPE with the Transformer block to pursue parameter efficiency. Utilizing the PEFT method, (IA)3 [188], MoV introduces tunable vectors that re-scale the Key and Value modules in the attention mechanism, as well as the activation within the FFN. By substituting conventional experts with (IA)3 vectors and updating only these lightweight experts and their corresponding gating during fine-tuning, MoV significantly reduces the computational burden associated with gradient calculations and lessens the memory footprint required for model storage. Similarly, MoLORA [42] employs multiple LoRA experts to the attention and FFN blocks, outperforming the standard LoRA approach. UniPELT [117] proposed a hybrid framework that integrates three representative PEFT methods as experts, namely Adapter [190], Prefixtuning [191], and LoRA [174]. Prefix-tuning is a method that freezes the base model and optimizes the continuous task-specific vectors prepended to the input of the attention. Within the UniPELT framework, LoRA matrices are applied to the weight matrices of Query and Key in the attention mechanism, Prefix vectors are added to the Key and Value modules, and the Adapter block is inserted after the FFN layer. UniPELT leverages different gating mechanisms to dynamically activate the experts, efficiently finding the approaches that best suit the given task.

4.3.3 Transformer模块

将MoPE与Transformer架构集成在近年研究中受到广泛关注。该方法涉及创建两组专家：一组用于注意力机制，另一组用于Transformer模块中的FFN。每组专家由其门控机制调节以控制专家的激活。如图6(c)所示，与Transformer块集成的MoPE框架下的正向过程可表示为：

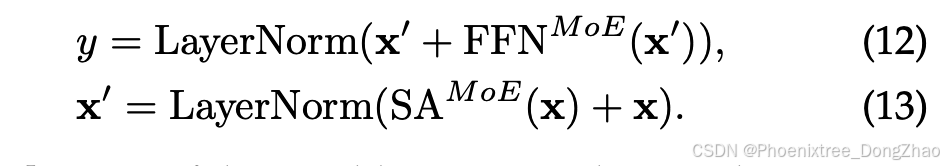
MoV是将MoPE与Transformer模块结合以实现参数效率的显著尝试之一。利用PEFT方法(IA)3 ，MoV引入了可调向量，重新缩放注意力机制中的Key和Value模块以及FFN中的激活。通过用(IA)3向量替代传统专家，并在微调时仅更新这些轻量级专家及其对应的门控，MoV显著减少了梯度计算的计算负担，并降低了模型存储所需的内存占用。类似地，MoLORA在注意力和FFN模块中采用了多个LoRA专家，表现优于标准LoRA方法。UniPELT提出了一个混合框架，集成了三种代表性的PEFT方法作为专家，分别是Adapter、Prefixtuning]和LoRA 。Prefix-tuning是一种冻结基础模型并优化附加到注意力输入前的连续任务特定向量的方法。在UniPELT框架中，LoRA矩阵应用于注意力机制中Query和Key的权重矩阵，Prefix向量添加到Key和Value模块，Adapter块插入FFN层后。UniPELT利用不同的门控机制动态激活专家，高效找到最适合给定任务的方法。

Further broadening the scope of the LoRA-MoE framework, Omni-SMoLA [43] extends the MoPE with three sets of LoRA experts, each tailored to handle text tokens, visual tokens, and multimodal tokens, respectively. The specialization enables the architecture to enhance performance across various vision-and-language tasks. In the context of MoPE research, the number of experts emerges as a critical hyperparameter influencing downstream task performance [42], [48]. Additionally, the use of many experts may lead to redundancy [192]. MoLA [118] is one of the pioneering work that explores the expert allocation issue. It proposes a LoRAMoE framework with a Layer-wise Expert Allocation, which enables the flexible employment of varying numbers of experts across different layers. The expert allocation strategy proposed by MoLA further improves the effectiveness of the LoRA-MoE framework. In the specialized field of medical applications, MOELoRA [119] tackles the challenges of task variety and high adaptation cost. It integrates LoRA experts and task-motivated gate functions into the attention and FFN of each layer. The gating utilizes task identity to modulate expert contributions, creating unique parameter sets tailored to individual tasks. The design of MOELoRA combines the strengths of both MoE and LoRA, strengthening LLM’s capability in medical domains. Liu et al. [120] design a novel framework, named Intuition-MoR1E, which leverages the inherent semantic clustering of instances to emulate cognitive processes in the human brain for multitasking purposes. This framework provides implicit guidance to the gating mechanism, thereby enhancing feature allocation. Furthermore, they introduce a cutting-edge rank1 expert architecture. This architecture advances beyond the conventional 1-1 mapping of two weight matrices W^i_up and W^i_down in LoRA expert composition, facilitating a flexible combination of any W^i_up with any W^j_down to form an expert. They implement MoE in the transformer blocks, specifically targeting the Query, Key, Value, and FFN modules. Xu et al. [121] present Multiple-Tasks Embedded LoRA (MeteoRA), a scalable and efficient framework that embeds multiple task-specific LoRA adapters into the base LLM using a fullmode MoE architecture. This framework incorporates custom GPU kernel operators to accelerate LoRA computation while maintaining memory overhead.

进一步扩展LoRA-MoE框架的范围，Omni-SMoLA通过三组LoRA专家扩展了MoPE，分别处理文本令牌、视觉令牌和多模态令牌。这种专业化使架构能够在各种视觉和语言任务中提升性能。在MoPE研究中，专家数量成为影响下游任务性能的关键超参数。此外，使用过多专家可能导致冗余。MoLA 是探索专家分配问题的开创性工作之一。它提出了一个具有层级专家分配的LoRAMoE框架，能够在不同层灵活使用不同数量的专家。MoLA提出的专家分配策略进一步提高了LoRA-MoE框架的有效性。在医学应用的专业领域，MOELoRA解决了任务多样性和高适应成本的挑战。它将LoRA专家和任务驱动的门控函数集成到每一层的注意力和FFN中。门控利用任务身份来调节专家贡献，创建针对个别任务的独特参数集。MOELoRA的设计结合了MoE和LoRA的优势，增强了LLM在医学领域的能力。Liu等人设计了一个名为Intuition-MoR1E的新框架，利用实例的固有语义聚类来模拟人脑的认知过程以实现多任务处理。该框架为门控机制提供了隐式指导，从而增强了特征分配。此外，他们引入了一种前沿的rank1专家架构。该架构超越了LoRA专家组成中两个权重矩阵W^i_up和W^j_down的1-1映射传统，促进了任何W^i_up与任何W^j_down的灵活组合以形成专家。他们在Transformer模块中实现了MoE，特别针对Query、Key、Value和FFN模块。Xu等人提出了Multiple-Tasks Embedded LoRA (MeteoRA)，一个可扩展且高效的框架，使用全模式MoE架构将多个任务特定的LoRA适配器嵌入到基础LLM中。该框架集成了自定义GPU内核操作符以加速LoRA计算，同时保持内存开销。

4.3.4 Every Layer

There has been considerable interest in incorporating MoPE into fundamental components such as the attention, FFN, and Transformer block. Existing work often approaches the attention mechanism and FFN independently, employing distinct gating mechanisms to modulate them separately. Rather than treating these elements isolated, there is a new direction that considers the Transformer layer as an integrated whole. This shift in perspective allows for the application of the MoPE framework to the entire Transformer layer, capturing the combined dynamics of the attention and FFN within a unified approach. As illustrated in Figure 6(d), the forward process under the MoPE framework integrated with every layer is as follows:

where ∆Wlayer and Glayer(x) is the parameter-efficient expert and gating function applied to the entire layer, respectively.

In this context, the approach presented by MoLE [48] provides innovative insights. MoLE identifies that various layers within LoRA exhibit unique features. In response to this finding, MoLE pursues to enhance the composition effect of trained LoRAs by dynamically adjusting the layerspecific weights according to the desired objective. This is achieved by integrating a set of trained LoRAs and a gating function into each layer. MoLE treats each layer of trained LoRAs as an individual expert and only trains the gating to learn the optimal composition weights for a specified domain. This dynamic linear composition strategy significantly extends the versatility of LoRA, enabling its application across a broader spectrum of practical scenarios.

4.3.4 每一层

将MoPE集成到注意力、FFN和Transformer模块等基本组件中引起了广泛兴趣。现有工作通常独立处理注意力机制和FFN，采用不同的门控机制分别调节它们。与其将这些元素孤立对待，新的方向是将Transformer层视为一个整体。这种视角的转变允许将MoPE框架应用于整个Transformer层，在统一的方法中捕捉注意力和FFN的联合动态。

在此背景下，MoLE提出的方法提供了创新见解。MoLE发现LoRA中的各个层具有独特特征。针对这一发现，MoLE通过根据目标动态调整层特定权重来增强训练后LoRA的组合效果。这是通过将一组训练后的LoRA和门控函数集成到每一层来实现的。MoLE将每一层训练后的LoRA视为独立专家，并仅训练门控以学习指定领域的最佳组合权重。这种动态线性组合策略显著扩展了LoRA的通用性，使其能够在更广泛的实际场景中应用。

4.4 Training & Inference Scheme

The architectural advancements of Mixture-of-Experts (MoE) models have been complemented by extensive research into training and inference schemes, with the objective of optimizing both computational efficiency and model quality.

Original Training & Inference Scheme. Initial training methodologies, as established in seminal works [8], [27], [28], [36], [37], involve constructing an MoE model and training it from scratch, with inference directly following the model configurations of training.

The advent of MoE models has introduced novel paradigms for training and inference, enabling a flexible approach that synergizes the strengths of dense and sparse models while mitigating their respective weaknesses. As depicted in Figure 7, we divide the emerging schemes into three distinct categories: Dense-to-Sparse, which entails initiating with dense model training and progressively transitioning to a sparse MoE configuration [49], [62], [64], [67], [106], [122], [123], [124]; Sparse-to-Dense, which involves degrading a sparse MoE model to a dense form that is more conducive to hardware implementation for inference [52], [53], [127]; and Expert Models Merging, a process of integrating multiple pretrained dense expert models into a unified MoE model [54], [129], [130].

4.4 训练与推理方案

混合专家（MoE）模型的架构进步得到了广泛的研究支持，这些研究旨在优化计算效率和模型质量。

原始训练与推理方案
早期的训练方法，如开创性工作[8][27][28][36][37]所述，涉及从头构建MoE模型并对其进行训练，推理阶段直接沿用训练时的模型配置。

MoE模型的引入带来了新的训练与推理范式，使得能够灵活结合稠密和稀疏模型的优势，同时缓解各自的不足。如图7所示，我们将新兴方案分为三类：

稠密到稀疏（Dense-to-Sparse）：从稠密模型训练开始，逐步过渡到稀疏MoE配置[49][62][64][67][106][122][123][124]
稀疏到稠密（Sparse-to-Dense）：将稀疏MoE模型简化为更适合硬件推理的稠密形式[52][53][127]
专家模型合并（Expert Models Merging）：将多个预训练的稠密专家模型整合为一个统一的MoE模型[54][129][130]

4.4.1 Dense-to-Sparse

To mitigate the training overhead associated with vision MoE transformer models, the Residual Mixture-of-Experts (RMoE) approach [122] commences with training a dense, non-MoE model on the upstream task, followed by an efficient fine-tuning stage to transition into a MoE model. This process reveals that directly inheriting expert weights from a pretrained non-MoE model’s FFN can lead to suboptimal performance, necessitating an alignment between the MoE and FFN outputs during the fine-tuning phase. Similarly, Dua et al. [123] advocate for initially training a dense model, subsequently introducing sparsity by incorporating a randomly initialized gating module, and further training the model’s feed-forward layers under sparsity conditions—specifically, by updating the weights locally within each compute node rather than averaging gradients across nodes.

Nie et al. [62] present EvoMoE, an efficient end-to-end MoE training framework. EvoMoE decouples the joint learning of experts and the sparse gate, emphasizing the acquisition of foundational knowledge through a single expert at the inception of training. Subsequently, it spawns multiple diverse experts and advances the diversification of experts by training with the novel Dense-to-Sparse gate (DTS-Gate). The DTS-Gate initially operates as a dense activation of all experts, then progressively and adaptively constricting to route tokens to a reduced number of experts. A similar strategy is employed in the development of the MoE-LLaVA [106] large vision-language model, which commences with a dense model, subsequently multiplies the feed-forward network (FFN) to create expert initializations, and proceeds to train exclusively the MoE layers, while keeping the remaining model components static.

Komatsuzaki et al. [49] highlight the efficiency of sparse models in terms of quality and computational cost, yet acknowledge their significant data requirements and the expense of training from scratch at scale. To address this, they introduce a scheme termed ”sparse upcycling,” which leverages pre-existing training investments by initializing a sparsely activated MoE model from a pretrained dense checkpoint. This involves transferring all parameters—and optionally their associated optimizer states—from the original checkpoint, with the exception of the MoE gating network parameters, which are not present in the dense model. Notably, the new MoE layers are populated with identical copies of the original dense model’s FFN layers, and the gating mechanism weights are initialized randomly. A critical obstacle in model upcycling is the initial performance decrease resulting from structural modifications to a trained network. To mitigate this performance regression during upcycling, the researchers propose normalizing the gating scores for each input token to 1, which are used to combine the outputs of multiple experts. This approach is grounded in the notion that, in the dense model, each token was processed by a singular “expert” FFN. While this normalization proved beneficial for upcycled vision models, it was found to be detrimental to the performance of upcycled language models. In the first introduction of sparse MoE by [27], the softmax function was applied to the selected top-k gating values, which normalizes the combination gating scores to 1, formulated as softmax(TopK(g(x; Θ), k)). However, subsequent LLMs [28], [36], [38] with MoE have evolved to apply the softmax function across all potential gating values before isolating the top-k subset, formulated as TopK(softmax(g(x; Θ)), k).

4.4.1 稠密到稀疏

为了缓解视觉MoE Transformer模型的训练开销，残差混合专家（RMoE）方法从在上游任务上训练稠密非MoE模型开始，随后通过高效微调阶段过渡到MoE模型。这一过程表明，直接从预训练的非MoE模型的FFN继承专家权重可能导致次优性能，因此需要在微调阶段对齐MoE和FFN的输出。类似地，Dua等人主张先训练稠密模型，随后通过引入随机初始化的门控模块引入稀疏性，并在稀疏条件下进一步训练模型的FFN层——具体来说，通过在每个计算节点内局部更新权重，而不是跨节点平均梯度。

Nie等人提出了EvoMoE，一种高效的端到端MoE训练框架。EvoMoE解耦了专家和稀疏门控的联合学习，强调在训练初期通过单一专家获取基础知识。随后，它生成多个多样化专家，并通过使用新颖的稠密到稀疏门控（DTS-Gate）训练推动专家的多样化。DTS-Gate最初以所有专家的稠密激活运行，随后逐步自适应地限制路由令牌的专家数量。类似的策略被用于开发MoE-LLaVA大型视觉语言模型，该模型从稠密模型开始，随后通过复制FFN创建专家初始化，并仅训练MoE层，同时保持其余模型组件不变。

Komatsuzaki等人强调了稀疏模型在质量和计算成本方面的效率，但也承认其显著的数据需求和大规模从头训练的开销。为了解决这一问题，他们引入了稀疏升级（sparse upcycling）方案，利用现有的训练投资，从预训练的稠密检查点初始化稀疏激活的MoE模型。这一过程涉及从原始检查点转移所有参数（以及可选的优化器状态），但稠密模型中不存在的MoE门控网络参数除外。值得注意的是，新的MoE层填充了原始稠密模型FFN层的相同副本，门控机制权重则随机初始化。模型升级中的一个关键障碍是由于对训练网络的修改导致的初始性能下降。为了缓解升级过程中的性能回归，研究者提出将每个输入令牌的门控分数归一化为1，用于组合多个专家的输出。这一方法基于稠密模型中每个令牌由单一“专家”FFN处理的假设。虽然这种归一化对升级的视觉模型有益，但发现对升级的语言模型性能有害。在[27]首次引入稀疏MoE时，对选定的top-k门控值应用了softmax函数，将组合门控分数归一化为1，公式为softmax(TopK(g(x; Θ), k))。然而，随后的LLMs演变为在所有潜在门控值上应用softmax函数，然后再隔离top-k子集，公式为TopK(softmax(g(x; Θ)), k)。

Building upon the sparse upcycling technique [49], the Skywork-MoE model [67] leverages the foundational architecture of its pre-developed Skywork-13B model [193], adopting its dense checkpoints as a foundation for initial states. Their empirical evidence indicates that the decision between sparse upcycling and training from scratch should be informed by both the performance of available dense checkpoints and the MoE-specific training resources, as models trained from scratch consistently surpass their upcycled counterparts in performance. The study observes a decline in average expert similarity throughout the training of upcycled MoEs, suggesting a diversification of experts emerges during the process. Importantly, the Skywork-MoE analysis reveals that models with greater expert similarity tend to underperform, establishing expert similarity as a potential diagnostic tool during MoE training for upcycled models. Conversely, the expert similarity in models trained from scratch remains minimal, implying that non-uniform expert initialization promotes diversification.

Pan et al. [64] posit that the parameter inefficiency observed in MoE models stems from conventional sparse training methodologies, where only a selected group of experts is engaged and refined for each input token. To counteract this, they introduce a hybrid framework for MoE models, denoted as DS-MoE, which integrates dense training (activating all the experts) with sparse inference (sparse expert activation) to achieve higher computation and parameter efficiency. Notably, DS-MoE maintains activation for all self-attention experts (MoA [82]) during inference but selectively activates FFN experts, reflecting the observation that self-attention layers manifest considerably less sparsity compared to FFN layers.

Chen et al. [124] introduce SMoE-Dropout, an innovative plug-and-play training framework, which initially modularizes the FFN into a sequence of smaller FFNs then employs a random policy parameterized by fixed weights to route token to k experts with the largest response. Progressively, the framework activates an increasing number of experts, preventing overfitting to the amounts of used network capacity during training. MoEfication [50] investigates various strategies for expert construction in T5 models, including random splitting, parameter clustering, and building co-activation graphs. MoEBERT [125] implements an importance-based method for adapting FFNs into experts within BERT models. LLaMA-MoE [51] conducts an extensive examination of different expert construction methods, ultimately proposing a straightforward random division approach that partitions the parameters of FFNs into non-overlapping experts. Emergent MoEs (EMoE) [126] splits certain FFN layers of the original model into MoE layers with clustering-based experts construction and avgk gating, which ameliorates the parameter updating during fine-tuning and can even be abandoned afterward to preserve the original model architecture.

基于稀疏升级技术，Skywork-MoE模型利用其预先开发的Skywork-13B模型的基础架构，采用其稠密检查点作为初始状态的基础。他们的实证表明，稀疏升级与从头训练之间的选择应基于可用稠密检查点的性能和MoE特定训练资源，因为从头训练的模型始终优于升级模型。研究观察到升级MoE训练过程中专家平均相似性的下降，表明专家在过程中逐渐多样化。重要的是，Skywork-MoE分析发现专家相似性较高的模型往往表现较差，专家相似性成为升级MoE训练中的潜在诊断工具。相反，从头训练的模型专家相似性始终较低，表明非均匀专家初始化促进了多样化。

Pan等人认为MoE模型中观察到的参数效率低下源于传统的稀疏训练方法，其中仅为每个输入令牌激活和优化选定的专家组。为了应对这一问题，他们引入了一种MoE模型的混合框架，称为DS-MoE，它结合了稠密训练（激活所有专家）和稀疏推理（稀疏专家激活）以实现更高的计算和参数效率。值得注意的是，DS-MoE在推理期间保持所有自注意力专家（MoA）的激活，但选择性激活FFN专家，反映了自注意力层相比FFN层表现出显著较低的稀疏性。

Chen等人引入了SMoE-Dropout，这是一种创新的即插即用训练框架。该框架首先将FFN模块化为一系列较小的FFN，然后采用由固定权重参数化的随机策略，将令牌路由到响应最大的k个专家。逐步地，该框架激活越来越多的专家，防止在训练过程中过度使用网络容量。MoEfication研究了T5模型中专家构建的各种策略，包括随机拆分、参数聚类和构建共激活图。MoEBERT采用了一种基于重要性的方法，将FFN适应为BERT模型中的专家。LLaMA-MoE对不同专家构建方法进行了广泛研究，最终提出了一种简单的随机划分方法，将FFN参数划分为非重叠的专家。Emergent MoEs（EMoE）将原始模型的某些FFN层拆分为基于聚类专家构建和avgk门控的MoE层，改善了微调期间的参数更新，甚至可以在之后放弃以保留原始模型架构。

4.4.2 Sparse-to-Dense

Switch Transformer [36] studies the distillation of large sparse models into smaller dense counterparts to achieve parameter efficiency for deployment. The study reports that initializing the corresponding weights of dense model from non-expert layers of MoE model modestly enhances performance, facilitated by the consistent dimension of nonexpert layers. Furthermore, an improvement in distillation is observed when employing a mixture of 0.25 for the teacher probabilities and 0.75 for the ground truth label. Leveraging both methods, the distillation preserves approximately 30% of the sparse model’s quality gains using only about 5% of the parameters. Similarly, Xue et al. [52] address the challenges of overfitting, deployment difficulty, and hardware constraints associated with sparse MoE models. Drawing inspiration from human learning paradigms, they propose a new concept referred to as ‘knowledge integration’ aimed at creating a dense student model (OneS) that encapsulates the expertise of a sparse MoE model. Their framework first implements knowledge gathering, explored through a variety of methods such as summation, averaging, topk Knowledge Gathering, and their Singular Value Decomposition Knowledge Gathering. Then, they refine the dense student model by knowledge distillation to mitigate noise introduced by the knowledge gathering. The OneS model retains 61.7% of the MoE’s benefits on ImageNet and 88.2% on NLP datasets. Further investigations into MoE model distillation are also conducted by other researchers [66], [78].

Chen et al. [53] highlight the challenges associated with deploying MoE models on resource-constrained platforms, such as cloud or mobile environments. Observing that only a fraction of experts contribute significantly to MoE finetuning and inference, they propose a method for the progressive elimination of non-essential experts. This approach retains the advantages of MoE while simplifying the model into a single-expert dense structure for the target downstream task. Similarly, ModuleFormer [73] applies a comparable pruning technique, removing task-unrelated experts for a lightweight deployment. Huang et al. [127] separate the training and inference stages for Vision Transformers (ViTs). They substitute certain FFNs in the ViT with customdesigned, efficient MoEs during training. These MoEs assign tokens to experts using a random uniform partition and incorporate Experts Weights Averaging (EWA) on these MoEs at the end of each iteration. After training, the MoEs are converted back to FFNs through averaging of expert weights, thus reverting the model to its original dense ViT for inference. He et al. [128] propose a unified framework for MoE model compression, encompassing two strategies: Expert Slimming, which compresses individual experts via pruning and quantization, and Expert Trimming, which structurally removes unimportant experts.

4.4.2 稀疏到稠密

Switch Transformer 研究了将大型稀疏模型蒸馏为小型稠密模型的方法，以实现部署时的参数效率。研究表明，从MoE模型的非专家层初始化稠密模型的相应权重，由于非专家层维度的一致性，能够适度提升性能。此外，当采用教师概率为0.25和真实标签为0.75的混合方法时，蒸馏效果有所改善。通过这两种方法，蒸馏过程仅使用约5%的参数，保留了稀疏模型约30%的质量增益。类似地，Xue等人解决了稀疏MoE模型在过拟合、部署困难和硬件约束方面的挑战。他们从人类学习模式中汲取灵感，提出了“知识整合”的新概念，旨在创建一个稠密学生模型（OneS），以封装稀疏MoE模型的专业知识。他们的框架首先实施知识收集，探索了多种方法，如求和、平均、top-k知识收集及其奇异值分解知识收集。然后，他们通过知识蒸馏精炼稠密学生模型，以减少知识收集引入的噪声。OneS模型在ImageNet上保留了MoE的61.7%的优势，在NLP数据集上保留了88.2%。其他研究者也对MoE模型蒸馏进行了进一步研究。

Chen等人强调了在资源受限平台（如云或移动环境）上部署MoE模型的挑战。观察到只有部分专家对MoE微调和推理有显著贡献，他们提出了一种逐步淘汰非必要专家的方法。该方法保留了MoE的优势，同时将模型简化为单一专家的稠密结构以适应目标下游任务。类似地，ModuleFormer 应用了类似的剪枝技术，移除与任务无关的专家以实现轻量级部署。Huang等人将视觉Transformer（ViT）的训练和推理阶段分离。他们在训练期间用定制设计的高效MoE替换ViT中的某些FFN。这些MoE使用随机均匀分区将令牌分配给专家，并在每次迭代结束时对这些MoE进行专家权重平均（EWA）。训练结束后，MoE通过专家权重平均转换回FFN，从而将模型恢复为原始的稠密ViT进行推理。He等人提出了一个统一的MoE模型压缩框架，包含两种策略：专家瘦身（通过剪枝和量化压缩单个专家）和专家修剪（从结构上移除不重要的专家）。

4.4.3 Expert Models Merging

Li et al. [129] introduce the Branch-Train-Merge (BTM) algorithm, a method for the communication-efficient training of language models (LMs). BTM independently trains a set of expert LMs (ELMs), each tailored to a specific domain within the training corpus, such as scientific or legal text. These ELMs, which operate without shared parameters, can be ensembled or parameter-averaged at inference to coalesce into a singular LM. Expanding on this concept, Sukhbaatar et al. [54] present Branch-Train-MiX (BTX), designed to combine the strengths of BTM and Mixture-ofExperts while addressing their respective limitations. BTX maintains separate training for multiple expert LLMs, akin to BTM, but subsequently integrates these experts within a unified MoE model. Specifically, it consolidates the FFNs from all ELMs into a singular MoE module at each layer, with a gating network determining the appropriate FFN expert for each token. Other components, such as the selfattention layers from ELMs, are merged by averaging their weights. The resulting model then undergoes MoE finetuning on all the combined data to enable the gate to effectively mix the FFN experts.

Wang et al. [130] point out that while the emergence of Foundation Models made it easier to obtain expert models tailored to specific tasks, the heterogeneity of data at test time necessitates more than a single expert. Accordingly, they explore the Fusion of Experts (FoE) challenge, which aims to integrate outputs from expert models that provide diverse but complementary insights into the data distribution, formulating it as an instance of supervised learning.

4.4.3 专家模型合并

Li等人引入了分支-训练-合并（BTM）算法，这是一种用于语言模型（LM）通信高效训练的方法。BTM独立训练一组专家语言模型（ELM），每个ELM针对训练语料库中的特定领域（如科学或法律文本）进行定制。这些ELM在训练时不共享参数，可以在推理时通过集成或参数平均合并为一个单一的语言模型。在此基础上，Sukhbaatar等人提出了分支-训练-混合（BTX），旨在结合BTM和混合专家的优势，同时解决它们各自的局限性。BTX像BTM一样独立训练多个专家LLM，随后将这些专家整合到一个统一的MoE模型中。具体来说，它在每一层将所有ELM的FFN合并为一个单一的MoE模块，并由门控网络决定每个令牌的适当FFN专家。其他组件（如ELM的自注意力层）通过权重平均合并。生成的模型随后在所有组合数据上进行MoE微调，以使门控能够有效混合FFN专家。

Wang等人指出，虽然基础模型的出现使得获取针对特定任务的专家模型变得更加容易，但测试时数据的异质性需要不止一个专家。因此，他们探索了专家融合（FoE）的挑战，旨在整合来自专家模型的输出，这些模型提供了对数据分布的多样但互补的见解，并将其公式化为监督学习的一个实例。

4.5 Derivatives

Building upon the principles of algorithm design highlighted earlier, numerous studies have drawn inspiration from the Mixture of Experts (MoE) framework, proposing a range of MoE variants. We categorize these innovative models as derivatives of the MoE. For instance, Xue et al. [58] introduced WideNet, an approach that increases model width by substituting the feed-forward network (FFN) with an MoE layer while maintaining shared trainable parameters across Transformer layers, except for the normalization layers. Subsequently, Tan et al. [59] presented the Sparse Universal Transformer (SUT), an efficient enhancement of the Universal Transformer, which is characterized by parameter-sharing across its layers. SUT incorporates a Sparse Mixture of Experts and a novel stick-breaking-based dynamic halting mechanism, thus reducing computational complexity without compromising parameter efficiency or generalization capabilities. Moreover, the traditional MoE models often employ discrete matching between experts and tokens [27], [28], [35], [36], [37], [94], [103], a practice associated with training instability and uneven expert utilization. To address these challenges, Antoniak et al. [56] innovatively proposes the Mixture of Tokens (MoT), which blends tokens from different examples before presenting them to the experts. Thus, MoT enables the model to benefit from a wider array of token-expert combinations.

Recently, the MoE’s principle of assigning specialized knowledge to individual experts has been adapted to parameter-efficient fine-tuning (PEFT). Choi et al. [60] propose the sparse mixture-of-prompts (SMoP), a method that utilizes a gating mechanism to train multiple short soft prompts, each adept at processing distinct subsets of data. This addresses the inefficiencies encountered with long soft prompts during prompt tuning. The MoE framework has also been integrated into lifelong learning (LLL), which seeks to facilitate continuous learning from an ongoing stream of data. The Lifelong-MoE model [55] dynamically expands model capacity by adding experts with regularized pretraining, effectively mitigating the issue of catastrophic forgetting [194] typically associated with straightforward fine-tuning. In a recent development, the MoE concept of conditional computation has been further refined to optimize resource allocation in transformer-based language models (LMs). The Mixture-of-Depths (MoD) [57] employs a binary gating network to decide whether a token should be processed by a given Transformer layer. As a result, MoD transformers can dynamically allocate computational resources (FLOPs) to specific sequence positions, achieving a lower overall FLOP footprint compared to vanilla or MoEbased transformers.

In summary, the evolution of MoE derivatives reveals a trend where models either integrate the conditional computation aspect of the gating mechanism or merge the MoE structure with various tasks achieved by assigning specialized knowledge to individual experts, such as aforementioned prompt tuning [60] and lifelong learning [55] with MoE, demonstrating the versatility and adaptability of the MoE architecture across different domains.

4.5 衍生模型

基于前述算法设计原则，许多研究从混合专家（MoE）框架中汲取灵感，提出了一系列MoE变体。我们将这些创新模型归类为MoE的衍生模型。

例如，Xue等人提出了WideNet，通过用MoE层替换前馈网络（FFN）来增加模型宽度，同时保持Transformer层之间共享可训练参数（归一化层除外）。随后，Tan等人提出了稀疏通用Transformer（SUT），这是对通用Transformer的高效增强，其特点是在各层之间共享参数。SUT结合了稀疏混合专家和一种新颖的基于stick-breaking的动态停止机制，从而在不影响参数效率或泛化能力的情况下降低计算复杂度。

此外，传统的MoE模型通常采用专家与令牌之间的离散匹配，这种做法与训练不稳定和专家利用不均衡相关。为了解决这些挑战，Antoniak等人创新性地提出了令牌混合（MoT），它在将令牌呈现给专家之前混合来自不同示例的令牌，从而使模型能够从更广泛的令牌-专家组合中受益。

最近，MoE将专业知识分配给单个专家的原则被应用于参数高效微调（PEFT）。Choi等人提出了稀疏提示混合（SMoP），该方法利用门控机制训练多个短软提示，每个提示擅长处理不同的数据子集，从而解决了长软提示在提示调优中的低效问题。

MoE框架还被集成到终身学习（LLL）中，旨在促进从持续数据流中持续学习。Lifelong-MoE模型通过添加具有正则化预训练的专家动态扩展模型容量，有效缓解了通常与直接微调相关的灾难性遗忘问题。

在最近的发展中，MoE的条件计算概念被进一步优化，以在基于Transformer的语言模型（LM）中优化资源分配。深度混合（MoD）采用二元门控网络决定令牌是否应由给定的Transformer层处理。因此，MoD Transformer可以动态地将计算资源（FLOPs）分配给特定的序列位置，与普通或基于MoE的Transformer相比，实现了更低的总体FLOP占用。

总之，MoE衍生模型的演变揭示了一种趋势，即模型要么集成了门控机制的条件计算方面，要么将MoE结构与通过将专业知识分配给单个专家实现的各种任务相结合，如上述提示调优和终身学习，展示了MoE架构在不同领域的多功能性和适应性。