练习:(点击打开链接)
1.汉罗塔问题。
2.斐波拉契数列
当n=0时,Fib[n]=0,当n=1时,Fib[n]=1,当n>1时,Fib[n]=Fib[n-1]+Fib[n-2]。
3.Stirling数
Stirling数,又称斯特灵数,在组合数学中,Stirling数可指两类数
第一类[编辑]
第一类Stirling数是有正负的,其绝对值是 个元素的项目分作
个元素的项目分作 个环排列的方法数目。常用的表示方法有
个环排列的方法数目。常用的表示方法有![s(n,k) , \left[\begin{matrix} n \\ k \end{matrix}\right]](http://upload.wikimedia.org/math/8/4/9/8494c8de074f7e71c7fbb634d3f83fd6.png) 。
。
换个较生活化的说法,就是有 个人分成
个人分成 组,每组内再按特定顺序围圈的分组方法的数目。例如
组,每组内再按特定顺序围圈的分组方法的数目。例如 :
:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {A},{B,D,C}
- {B},{A,C,D}
- {B},{A,D,C}
- {C},{A,B,D}
- {C},{A,D,B}
- {D},{A,B,C}
- {D},{A,C,B}
这可以用有向图来表示。
- 给定
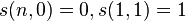 ,有递归关系
,有递归关系
递推关系的说明:考虑第n+1个物品,n+1可以单独构成一个非空循环排列,这样前n种物品构成k-1个非空循环排列,方法数为s(n,k-1);也可以前n种物品构成k个非空循环排列,而第n+1个物品插入第i个物品的左边,这有n*s(n,k)种方法。
 是调和数的推广。
是调和数的推广。
 是递降阶乘多项式的系数:
是递降阶乘多项式的系数:
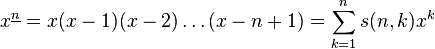
第二类[编辑]
第二类Stirling数是 个元素的集定义k个等价类的方法数目。常用的表示方法有
个元素的集定义k个等价类的方法数目。常用的表示方法有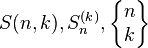 。(把包含N个元素的集合划分为正好K个非空子集的方法的数目)
。(把包含N个元素的集合划分为正好K个非空子集的方法的数目)
换个较生活化的说法,就是有 个人分成
个人分成 组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此
组的分组方法的数目。例如有甲、乙、丙、丁四人,若所有人分成1组,只有所有人在同一组这个方法,因此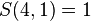 ;若所有人分成4组,只可以人人独立一组,因此
;若所有人分成4组,只可以人人独立一组,因此 ;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
;若分成2组,可以是甲乙一组、丙丁一组,或甲丙一组、乙丁一组,或甲丁一组、乙丙一组,或其中三人同一组另一人独立一组,即是:
- {A,B},{C,D}
- {A,C},{B,D}
- {A,D},{B,C}
- {A},{B,C,D}
- {B},{A,C,D}
- {C},{A,B,D}
- {D},{A,B,C}
因此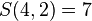 。
。
- 给定
 ,有递归关系
,有递归关系
- 递推关系的说明:考虑第n个物品,n可以单独构成一个非空集合,此时前n-1个物品构成k-1个非空的不可辨别的集合, 方法数为S(n-1,k-1);也可以前n-1种物品构成k个非空的不可辨别的 集合,第n个物品放入任意一个中,这样有k*S(n-1,k)种方法。




 是二项式系数,B_n是贝尔数。
是二项式系数,B_n是贝尔数。
4.Catalan数 HDU1023(点击打开链接)
卡特兰数又称卡塔兰数,英文名Catalan number,是组合数学中一个常出现在各种计数问题中出现的数列。由以比利时的数学家欧仁·查理·卡塔兰 (1814–1894)命名,其前几项为 : 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
2原理编辑
3应用编辑
括号化
出栈次序
凸多边形三角划分
给定节点组成二叉树
4扩展编辑
5C++应用编辑
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
|
void
catalan()
//求卡特兰数
{
int
i, j, len, carry, temp;
a[1][0] = b[1] = 1;
len = 1;
for
(i = 2; i <= 100; i++)
{
for
(j = 0; j < len; j++)
//乘法
a[i][j] = a[i-1][j]*(4*(i-1)+2);
carry = 0;
for
(j = 0; j < len; j++)
//处理相乘结果
{
temp = a[i][j] + carry;
a[i][j] = temp % 10;
carry = temp / 10;
}
while
(carry)
//进位处理
{
a[i][len++] = carry % 10;
carry /= 10;
}
carry = 0;
for
(j = len-1; j >= 0; j--)
//除法
{
temp = carry*10 + a[i][j];
a[i][j] = temp/(i+1);
carry = temp%(i+1);
}
while
(!a[i][len-1])
//高位零处理
len --;
b[i] = len;
}
}
|












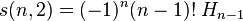
![s(n,3) = \frac{1}{2} (-1)^{n-1} (n-1)! [ (H_{n-1})^2 - H_{n-1}^{(2)} ]](http://upload.wikimedia.org/math/8/b/0/8b074a8e91fdb536ac2e87387cf3ff12.png)


















 1689
1689

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








