离散数学（九）：集合的基本概念和运算

1、集合

1.1 集合的定义

一些离散个体组成的全体，组成集合的个体称为它的元素或成员。

1.2 集合的表示

列元素法    A = { a, b, c, d }

谓词表示法  B = { x | P(x) }         B 由使得 P(x) 为真的 x 构成

1.3 集合与元素的关系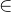：属于，不属于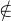

 实例：   

         A={ x | xRx2-1=0 },  A={-1,1}

         1A,  2A

注意：对于任何集合 A 和元素 x (可以是集合)，

            xA和 xA 两者成立其一，且仅成立其一.  

1.4 集合之间的关系

 

 1.5 空集与全集

 1.6 幂集

 2、集合的基本运算

2.1 集合运算的定义

 2.2 集合运算的说明

 2.3 集合运算的算律

 

 2.4 应用：集合包含或相等的证明方法

2.4.1 证明集合包含

(1) 命题演算法

(2) 包含传递法

 

(3) 等价条件法

(4) 反证法

 (5) 并交运算法

2.4.2 证明集合相等

(1) 命题演算

(2) 等式代入法

(3) 反证法

 (4) 运算法