统计学习方法笔记：逻辑斯谛回归与最大熵模型（下）

1.3模型学习的最优化算法

逻辑斯谛回归模型、最大熵模型学习归结为以似然函数为目标函数的最优化问题，通常通过迭代算法求解。从最优化的观点看，这时的目标函数具有很好的性质。它是光滑的凸函数，因此多种最优化的方法都适用，保证能找到全局最优解。常用的方法有迭代尺度法、梯度下降法、牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。

1.3.1改进的迭代尺度法

改进的迭代尺度法（improved iterative scaling,IIS）是一种最大熵模型学习的最优化算法。

已知最大熵模型为

对数似然函数为

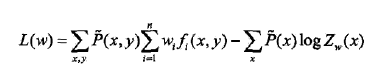
目标是通过极大似然估计学习模型参数，即求对数似然函数的极大值w^.

IIS的想法是：假设最大熵模型当前的参数向量使w=(w1,w2,…,wn)T,我们希望找到一个新的

参数向量w+δ=(w1+δ1, w2+δ2,…,wn+δn)T,使得模型的对数似然函数值增大。如果能有这样一种参数向量更新的方法,那么就可以重复使用这一方法，直至找到对数似然函数的最大值。

对于给定的经验分布P~(x,y)，模型参数从w到w+δ，对数似然函数的改变量是

建立对数似然函数改变量的下界：

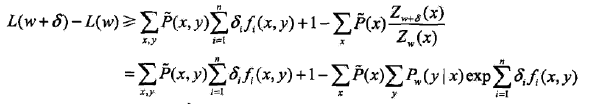
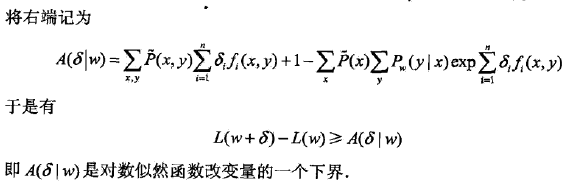
如果能找到适当的δ使下界A(δ|w)提高，那么对数似然函数也会提高。然而，函数A(δ|w)中的δ是一个想想，含有多个变量，不易同时优化。IIS试图只优化其中一个变量δi，而固定其他变量δj，i!=j.

为了达到这一目的，IIS进一步降低下界A(δ|w)。具体地，IIS引进一个f#(x,y)

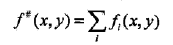
因为fi是二值函数，故f#(x,y)表示所有特征在(x,y)出现的次数。这样，A(δ|w)可以改写为

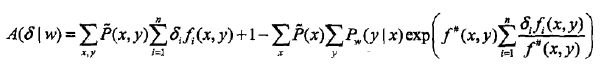
利用指数函数的凸性以及对任意I,有

这一事实，根据Jesen不等式，得到

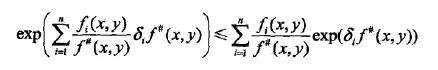
于是上式可改写为

记不等式右端为

于是得到

这里，B(δ|w)是对数似然函数改变量的一个新的（相对不紧的）下界。

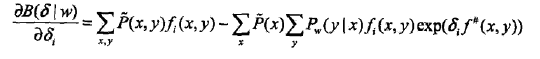
除δi外不含任何其他变量。令偏导数为0得到

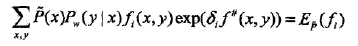
改进的迭代尺度算法IIS

输入：特征函数f1,f2,…,fn;经验分布P~(X,Y)，模型Pw(y|x)

输出：最优参数值w*I;最优模型Pw

这一算法关键一步是（a），即求解方程中的δi,.如果f#(x,y)是常数，即对任何x,y，有f#(x,y)=m,那么δi可以显式地表示成

如果f#(x,y)不是常数，那么必须通过数值计算求δi。简单有效的方法是牛顿法。以g(δi)=0表示方程，牛顿法通过迭代求得δ*i，使得g(δ*i)=0，迭代公式是

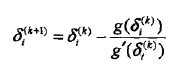
只要适当选取初始值δ（0）i，由于δi的方程有单根，因此牛顿法恒收敛，而且收敛速度很快。

1.3.2拟牛顿法

最大熵模型学习还可以应用牛顿法或拟牛顿法，详情请自行百度哈。
对于最大熵模型而言，

目标函数：

 

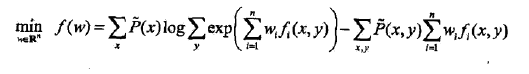
梯度：

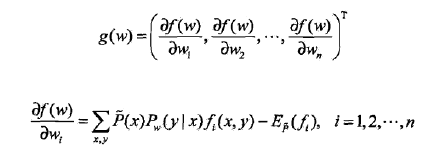
最大熵模型学习的BFGS算法

输入：特征函数f1,f2,…,fn    ;经验分布P~(x,y),目标函数f(w),梯度g(w)=,精度要求ε

输出：最优参数值w*;最优模型Pw(y|x)