深度学习-神经元（neuron）与感知机（perceptron）

一，神经元模型

神经元模型是神经网络中最基本的组成成分（这一概念来源于生物神经网络中，通过电位变化表示“兴奋”的生物神经元。）

后来将此生物活动抽象为”M-P神经元模型“，通过对n个输入信号，通过带权重的连接（connection）进行传递，将总的输入与阈值进行比较，通过“激活函数”处理产生输出。

其中，理想的激活函数为Sgn（阶跃函数），但其不光滑，不连续的性质，实际多采用Sigmoid函数。

二，感知机

感知机是基础的线性二分类模型（即输出为两个状态），由两层神经元组成。

并且感知机只有输出层神经元进行激活函数处理，即只拥有一层功能神经元。（这限制了它的学习能力）

（这样看，其实M-P神经元与感知机可以说是一种东西。）

用感知机可以很方便的实现与、或、非运算（网上例子很多），但不能处理线性不可分的问题（如异或）。

处理方法很简单，多加一层功能神经元就能解决异或问题。如下图所示

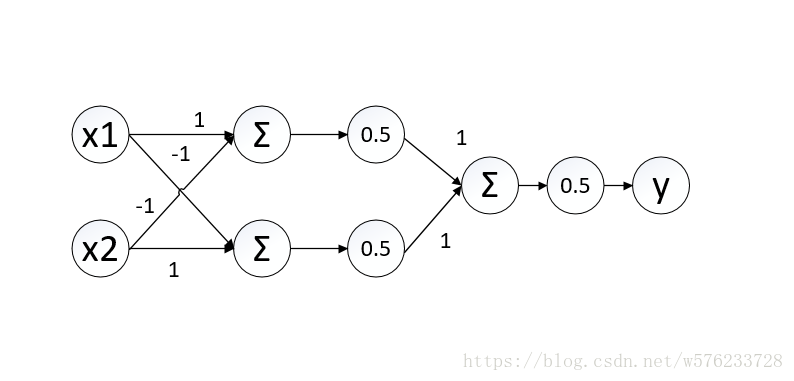
输入层与输出层之间的一层神经元被称为隐藏层或隐含层（hidden layer）。

结语

神经元（感知机）是组成神经网络的最基本成分，只需包含隐藏层，即可称为多层网络。神经网络训练的结果可以说就是连接权与阈值。