承接上一篇博客
https://blog.csdn.net/waitingwinter/article/details/106164350
为了使结构完整,我们再次给出所求解的问题:
{
−
U
′
′
(
t
)
+
U
(
t
)
=
(
π
2
+
1
)
sin
π
t
,
U
(
0
)
=
U
(
1
)
=
0
,
\left\{ \begin{aligned} & -U''(t) +U(t) = (\pi^2 + 1)\sin \pi t,\\ & U(0)=U(1) =0, \end{aligned} \right.
{−U′′(t)+U(t)=(π2+1)sinπt,U(0)=U(1)=0,
二次有限元
数值格式
与之前有所不同的是, 我们取检验函数空间为
V
=
H
0
2
(
Ω
)
V=H_0^2(\Omega)
V=H02(Ω),
将区间 [0,1] 等分为 N 个网格, 记
t
i
=
i
/
N
,
t_i =i/N,
ti=i/N, 故有
t
0
=
0
,
t
N
=
1.
t_0=0,t_N=1.
t0=0,tN=1. 令
h
i
=
t
i
−
t
i
−
1
h_i = t_i-t_{i-1}
hi=ti−ti−1 为网格尺寸. 因为等分网格, 故
h
i
=
h
=
1
/
N
,
∀
i
.
h_i=h=1/N,\,\forall\,i.
hi=h=1/N,∀i. 取基函数
Φ
i
(
i
=
2
,
3
,
⋯
,
N
−
2
)
\Phi_i(i=2,3,\cdots,N-2)
Φi(i=2,3,⋯,N−2) 为分片二次函数.
引理:
对于分片多项式函数
v
v
v,
v
∈
H
2
(
Ω
)
⇔
v
∈
C
1
(
Ω
ˉ
)
.
v\in H^2(\Omega)\Leftrightarrow v\in C^1(\bar{\Omega}).
v∈H2(Ω)⇔v∈C1(Ωˉ).
由上述引理知, 我们要构造整体
C
1
C^1
C1 的二次元, 故
Φ
\Phi
Φ 不能为如下形式
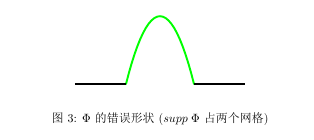
Φ
i
(
t
)
=
{
(
t
−
t
i
−
1
)
2
h
2
,
t
∈
(
t
i
−
1
,
t
i
]
,
(
t
i
+
1
−
t
)
2
h
2
,
t
∈
(
t
i
,
t
i
+
1
]
,
0
,
o
t
h
e
r
w
i
s
e
.
\Phi_i(t)=\left\{ \begin{aligned} &\frac{(t-t_{i-1})^2}{h^2},& t\in (t_{i-1}, t_i],\\ &\frac{(t_{i+1}-t)^2}{h^2},&t\in (t_i,t_{i+1}],\\ &0,&otherwise. \end{aligned} \right.
Φi(t)=⎩⎪⎪⎪⎪⎨⎪⎪⎪⎪⎧h2(t−ti−1)2,h2(ti+1−t)2,0,t∈(ti−1,ti],t∈(ti,ti+1],otherwise.
这里我采取了如下构造方式
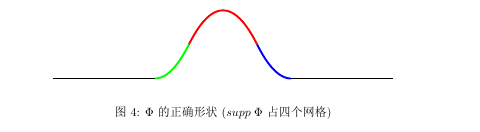
Φ
i
(
t
)
=
{
(
t
−
t
i
−
2
)
2
2
h
2
,
t
∈
(
t
i
−
2
,
t
i
−
1
]
,
−
(
t
i
−
t
)
2
2
h
2
+
1
,
t
∈
(
t
i
−
1
,
t
i
+
1
]
,
(
t
−
t
i
+
2
)
2
2
h
2
,
t
∈
(
t
i
+
1
,
t
i
+
2
]
,
0
,
o
t
h
e
r
w
i
s
e
.
\Phi_i(t)=\left\{ \begin{aligned} &\frac{(t-t_{i-2})^2}{2h^2},& t\in (t_{i-2}, t_{i-1}],\\ &\frac{-(t_{i}-t)^2}{2h^2}+1,&t\in (t_{i-1},t_{i+1}],\\ &\frac{(t-t_{i+2})^2}{2h^2}, &t\in (t_{i+1},t_{i+2}],\\ &0,&otherwise. \end{aligned} \right.
Φi(t)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧2h2(t−ti−2)2,2h2−(ti−t)2+1,2h2(t−ti+2)2,0,t∈(ti−2,ti−1],t∈(ti−1,ti+1],t∈(ti+1,ti+2],otherwise.
令
K
i
j
=
∫
0
1
Φ
i
′
(
t
)
Φ
j
′
(
t
)
+
Φ
i
(
t
)
Φ
j
(
t
)
d
t
,
K_{ij}=\int_0^1 \Phi_i'(t)\Phi_j'(t)+\Phi_i(t)\Phi_j(t)\,dt,
Kij=∫01Φi′(t)Φj′(t)+Φi(t)Φj(t)dt, 经计算有
K
i
j
=
{
4
3
h
+
23
15
h
,
i
=
j
,
119
h
120
+
1
6
h
∣
i
−
j
∣
=
1
,
7
h
30
−
2
3
h
∣
i
−
j
∣
=
2
,
h
120
−
1
6
h
∣
i
−
j
∣
=
3
,
0
,
o
t
h
e
r
w
i
s
e
.
K_{ij}=\left\{\begin{aligned} &\frac{4}{3h}+\frac{23}{15}h,&i=j,\\ &\frac{119h}{120}+\frac{1}{6h}&|i-j|=1,\\ &\frac{7h}{30}-\frac{2}{3h}&|i-j|=2,\\ &\frac{h}{120}-\frac{1}{6h}&|i-j|=3,\\ &0,&otherwise. \end{aligned} \right.
Kij=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎧3h4+1523h,120119h+6h1307h−3h2120h−6h10,i=j,∣i−j∣=1,∣i−j∣=2,∣i−j∣=3,otherwise.
令
f
j
=
∫
0
1
(
π
2
+
1
)
sin
π
t
Φ
j
(
t
)
d
t
,
f_j = \int_0^1 (\pi^2+1)\sin \pi t \,\Phi_j(t)\,\mathrm{d} t,
fj=∫01(π2+1)sinπtΦj(t)dt,
则有
f
j
=
4
(
π
2
+
1
)
h
2
π
3
(
1
−
cos
h
π
)
sin
h
π
sin
(
π
t
j
)
,
j
=
2
,
⋯
,
N
−
2.
f_j =\frac{4(\pi^2+1)}{h^2\pi^3}(1-\cos h\pi)\sin h\pi \sin(\pi t_j), \quad j=2,\cdots,N-2.
fj=h2π34(π2+1)(1−coshπ)sinhπsin(πtj),j=2,⋯,N−2.
记
u
=
[
u
2
,
u
3
⋯
,
u
N
−
2
]
T
u=[u_2,u_3\cdots,u_{N-2}]^T
u=[u2,u3⋯,uN−2]T,
F
=
[
f
2
,
f
3
,
⋯
,
f
N
−
2
]
T
,
F = [f_2,f_3,\cdots,f_{N-2}]^T,
F=[f2,f3,⋯,fN−2]T, 求解线性方程组
K
u
=
F
,
Ku=F,
Ku=F,
注意到此矩阵为七对角矩阵, 用MATLAB求得方程的数值解
U
h
(
t
)
=
∑
i
=
2
N
−
2
u
i
Φ
i
(
t
)
.
U_h(t)=\sum_{i=2}^{N-2}u_i\Phi_i(t).
Uh(t)=i=2∑N−2uiΦi(t).
解常微分方程, 容易求得问题的解为
U
(
t
)
=
sin
π
t
.
U(t)=\sin \pi t.
U(t)=sinπt.

需要注意的是,解出来的数值解是分片二次插值,所以严格来说,我的图中线性点与点线性插值是错误的.
误差估计
误差仍然采用之前的
∥
e
∥
=
∫
Ω
∣
u
′
(
t
)
−
u
h
′
(
t
)
∣
2
d
t
,
\Vert e\Vert =\int_{\Omega}|u'(t)-u_h'(t)|^2\,\mathrm{d}t,
∥e∥=∫Ω∣u′(t)−uh′(t)∣2dt,
这个积分最好借助Mathematica来算(不太友好)。
数值实验结果如下图 所示, 使用 polyfit 拟合图像斜率有
k
=
−
0.9304
,
k=-0.9304,
k=−0.9304,
即二次元的数值误差阶为 0.9304.

MATLAB代码
%% Quadratic function interpolation
err = zeros(8, 1);
n=10;
index = zeros(8,1);
for i=1:8
index(i) = 2^(i-1) *n;
end
err_new = zeros(8,1);
for i = 1:8
N = index(i);
h = 1 / N;
x = 0:h:1;
xx = 0:1/1000:1;
exact_solu = sin(pi.*xx);
K = zeros(N-3);
K = K + diag(ones(N-3,1).*(4/(3*h)+23/15*h), 0) + diag((119*h/120+1/(6*h)).*ones(N-4,1), 1) + diag((119*h/120+1/(6*h)).*ones(N-4,1), -1)+...
diag((7*h/30-2/(3*h)).*ones(N-5,1), -2)+diag((7*h/30-2/(3*h)).*ones(N-5,1), 2)+diag((h/120-1/(6*h)).*ones(N-6,1), -3)+diag((h/120-1/(6*h)).*ones(N-6,1), 3);
F = (pi^2+1)/(h^2*pi^3)*4*(1-cos(h*pi))*sin(pi*h)*sin(pi*x(3:N-1));
K = sparse(K);
coeff = K\F';
solu = [0; 0; coeff; 0; 0] + 0.5.*[0; coeff; 0; 0; 0] + 0.5 * [0; 0; 0; coeff; 0];
figure()
plot(x', solu, '*--',xx', exact_solu, 'g--');
legend('numerical solution', 'exact solution')
xlabel('x')
ylabel('U');
% ylim([0,1]);
title(['numerical solution and exact solution N=',num2str(index(i))]);
% calculate the error
% 形式太复杂了, 尽管借助了mathematica, 但还是很不爽
error = 0;
% 中间的 N-6块
for j = 4 :1: (N-3)
a = coeff(j);
b = coeff(j-1);
c = coeff(j-2);
d = coeff(j-3);
t = x(j);
t_h = x(j+1);
error = error + 1/(12*h^2*pi)*(24*(a-b-c+d)*(cos(pi*t)-cos(pi*(t_h)))+h*pi*...
(4*a^2+4*a*b+4*b^2-8*a*c-4*b*c+4*c^2-4*a*d-8*b*d+4*c*d+4*d^2+6*h^2*pi^2+24*(b-d)*sin(pi*t)...
+3*h*pi*(sin(2*pi*(t_h))-sin(2*pi*t))+24*(c-a)*sin(pi*(t_h))));
end
% 左边的3块
a = coeff(1);
b = coeff(2);
c = coeff(3);
error1 = 1/(6*h^2*pi)*(12*a+2*a^2*h*pi+3*h^3*pi^3-12*a*cos(h.*pi)+3*h.*pi*(-4*a+h.*pi.*cos(h.*pi))*sin(pi.*h));
error2 = 1/(12*h^2*pi)*(-24*(a+b)*cos(h*pi)+24*(a+b)*cos(2*h*pi)+...
h*pi*(4*a^2-4*a*b+4*b^2+6*h^2*pi+24*a*sin(h*pi)+3*(8*b-h*pi)*sin(2*h*pi)+3*h*pi*sin(4*h*pi)));
error3 = 1/(12*h^2*pi)*(24*(a+b-c)*(cos(3*h*pi)-cos(2*h*pi))+h*pi*(...
4*a^2-4*a*b+4*b^2-8*a*c+4*b*c+4*c^2+6*h^2*pi^2+24*b*sin(2*h*pi)+24*(a-c)*sin(3*h*pi)+3*h*pi*(sin(6*h*pi)-sin(4*h*pi))));
% 右边的3块(其实是相等的)
a = coeff(N-3);
b = coeff(N-4);
c = coeff(N-5);
error_1 = 1/(6*h^2*pi)*(12*a+2*a^2*h*pi+3*h^3*pi^3-12*a*cos(h.*pi)+3*h.*pi*(-4*a+h.*pi.*cos(h.*pi))*sin(pi.*h));
error_2 = 1/(12*h^2*pi)*(-24*(a+b)*cos(h*pi)+24*(a+b)*cos(2*h*pi)+...
h*pi*(4*a^2-4*a*b+4*b^2+6*h^2*pi+24*a*sin(h*pi)+3*(8*b-h*pi)*sin(2*h*pi)+3*h*pi*sin(4*h*pi)));
error_3 = 1/(12*h^2*pi)*(24*(a+b-c)*(cos(3*h*pi)-cos(2*h*pi))+h*pi*(...
4*a^2-4*a*b+4*b^2-8*a*c+4*b*c+4*c^2+6*h^2*pi^2+24*b*sin(2*h*pi)+24*(a-c)*sin(3*h*pi)+3*h*pi*(sin(6*h*pi)-sin(4*h*pi))));
err(i) = error + error1 + error2 + error3 + error_1 + error_2 + error_3;
end
figure()
plot(log2(err),'o--');
title('二次元误差阶')
xlabel('N')
ylabel('$log_{2}Error$', 'Interpreter','LaTex')
xlim([0.8,8.2])
ylim([-6.2,0.8])
axis on;
set(gca,'xtick',1:1:8);
set(gca,'xticklabel',{10,20,40,80,160,320,640,1280});
[order,~] = polyfit(1:1:(length(err)), log2(err)', 1);
disp(order)






















 2884
2884











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








