NeRF理解-- Nerf采样策略

Roo4ie

已于 2023-09-30 22:36:17 修改

阅读量671

点赞数 4

分类专栏： Nerf 文章标签：计算机视觉算法

于 2023-09-30 22:33:30 首次发布

本文链接：https://blog.csdn.net/wang1143790045/article/details/133443414

版权

Nerf 专栏收录该内容

3 篇文章 0 订阅

订阅专栏

主要内容参考以下链接，为方便NeRF学习做的相关记录。感谢以下博主的精彩文章！

参考链接：
https://zhuanlan.zhihu.com/p/478685602

https://blog.csdn.net/anshuai_aw1/article/details/82626468

https://zhuanlan.zhihu.com/p/146144853

https://www.scratchapixel.com/lessons/mathematics-physics-for-computer-graphics/monte-carlo-methods-in-practice/monte-carlo-integration.html

https://zhuanlan.zhihu.com/p/396618080

基本概念回顾（PDF、CDF、蒙特卡洛积分）

2.1 离散型随机变量的概率函数和概率分布

研究一个随机变量，不只是要看它能取哪些值，更重要的是它取各种值的概率如何！–陈希孺

2.1.1 离散型随机变量的概率质量函数(PMF)

离散型随机变量的概率质量函数就是用函数的形式来表达概率。比如:
$p_i=P(X=a_i),i=1,2,3,4,5,6$
在这个函数里，自变量 $X$ 是随机变量的取值，因变量 $p_i$ 是取值的概率。它就代表了每个取值的概率，所以顺理成章的它就叫做 $X$ 的概率质量函数。从公式上来看，概率质量函数一次只能表示一个取值的概率。比如 $P(X=1)=\frac{1}{6}$ ，这代表用概率函数的形式来表示，当随机变量取值为1的概率为1/6，一次只能代表一个随机变量的取值。

2.1.2 离散型随机变量的概率分布

概率分布的关键在于分布两个字，为了理解分布，看下面表格:

上面的分布列表叫做离散型随机变量的“概率分布”。其实严格来说，它应该叫离散型随机变量的值分布和值的概率分布列表，因为列表上面是值，下面是这个取值相应取到的概率，而且这个列表把所有可能出现的情况全部都列了出来。

举个例子，一颗6面的骰子，有1，2，3，4，5，6这6个取值，每个取值取到的概率都为1/6。那么下面的列表就不是骰子取值的”概率分布“，因为并没有将所有的取值全部列出来，下表中少了6这个值。

2.1.3 概率分布函数(CDF)

设离散型随机变量 $X$ 的分布律是 $P\{X=X_k\}=p_k,k=1,2,3...$ ，则 $F(x)=P(X\leq x)=\sum_{x_i\leq x}p_k$ 。由于 $F (x)$ 是 $X$ 取 $\leq x$ 的所有 $x_k$ 的概率之和，所以称 $F (x)$ 为累积概率函数。概率分布函数是概率函数取值的累加结果，所以又称为累积分布函数。

2.2 连续型随机变量的概率密度函数(PDF)和累积分布函数(CDF)

连续型随机变量的概率函数和分布函数与离散型随机变量的概率函数是不一样的，"密度函数"的由来可解释如下，取一个点 $x$ ,

按分布函数的定义，事件 $\leq x+h|$ 的概率( $h > 0$ 为常数)，应为 $F (x + h) - F (x)$ ，所以比值 $[F (x + h) - F (x)] / h$ 可以解释为在 $x$ 点附近 $h$ 这么长的区间 $(x, x + h)$ 内，单位长所占有的概率，令 $\rightarrow 0$ 则这个比的极限即 $F^{'} (x) = f (x)$ ，也就是在 $x$ 点处(无穷小区段内)单位长的概率，或者说它反映了概率在 $x$ 点处的“密集程度”，可以设想一条极细的无穷长的金属杆，总质量为1，概率密度相当于杆上各点的质量密度。具体公式如下:
$\leq X \leq b)=F(b)-F(a)=\int^a_b x dx$
概率密度函数用数学公式表示就是一个定积分的函数，定积分在数学中是用来求面积的，在这里就把概率表示为面积即可！
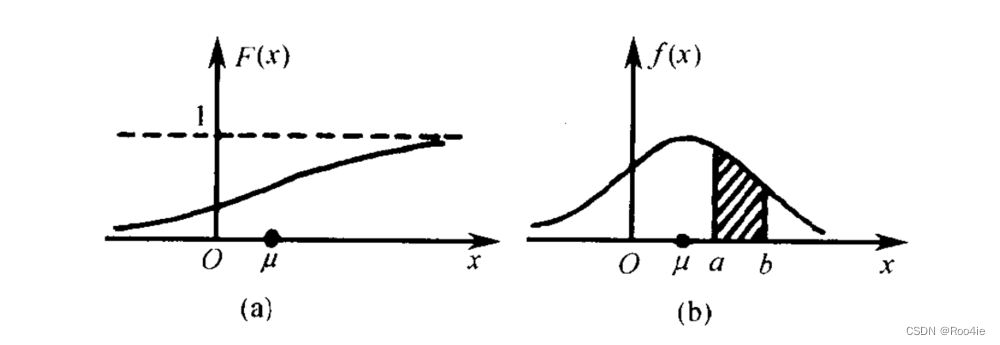
在这里插入图片描述
图(a) $F (x)$ 连续型随机变量分布函数画出的图形，图(b)是 $f (x)$ 连续型随机变量的概率密度函数画出的图像，它们之间的关系就是，概率密度函数是分布函数的导函数。两张图对比发现，如果用图(b)中的面积来表示概率，利用图形就能很清楚的看出，哪些取值的概率更大！所以，我们在表示连续型随机变量的概率时，用f(x)概率密度函数来表示是非常有效的。

2.3 蒙特卡洛方法

蒙特卡洛方法是一类通过随机采样来求解问题的算法的统称，要求解的问题是某随机事件的概率或某随机变量的期望。通过随机抽样的方法，以随机事件出现的频率估计其概率，并将其作为问题的解。下文主要介绍蒙特卡洛方法在积分计算上的应用。
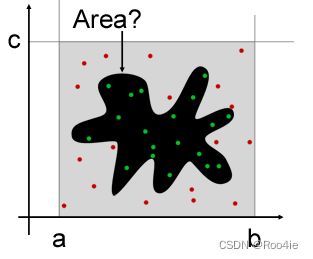
在这里插入图片描述

蒙特卡洛的基本做法是通过大量重复试验，通过统计频率来估计概率，从而得到问题的求解。举个例子，如上图所示，一个矩形内有一个不规则图案，要求解不规则图形的面积。显然，矩形的面积可以简单计算为 $A = ab \times a c$ ，点位于不规则形状内的概率为 $p=\frac{A_{shape}}{A}$ 。现在重复往矩形范围内随机的投射点，样本点有一定概率会落在不规则图形内，若复杂n次试验，落到不规则图形内的次数为k，频率为k/n，若样本数量较大，则有:
$p=\frac{A_{shape}}{A}\approx\frac{k}{n} \tag{2.1}$
根据伯努利大数定理得到的结论就是：随着样本数增加，频率 $\frac{k}{n}$ 会收敛于概率 $p$ ，使得该等式成立。因此，我们可以估计出不规则图形的面积为 $A\frac{k}{n}$ 。假设矩形面积为1，投射了1000次，有200个点位于不规则形状内，则可以推算出不规则图形的面积为0.2，投射的次数越大，计算出来的面积越精确。蒙特卡洛方法的求解的结果是有误差的，重复的试验越多误差就会越低。

2.3.1 积分估计

蒙特卡洛方法的一个重要应用就是求定积分，如下图函数 $f (x)$ 在区间 [a,b] 上的积分可以看作曲线下的面积，但实际求解过程中原函数可能很难求出，蒙特卡洛方法采用如下方式计算，在 $[a, b]$ 之间随机取一点x时，它对应的函数值就是 $f (x)$ ，那么就可以用 $f (x) \times (b - a)$ 来粗略估计曲线下方的面积，也就是需要求的积分值，当然这种估计（或近似）是非常粗略的。
在这里插入图片描述

但是不断在不同的随机点取值，并利用 $f (x) \times (b - a)$ 估算矩形的面积，最后将矩形的面积相加并取平均值，最终采样的次数越多得到的估算平均值会越来越接近函数 $f (x)$ 积分的实际结果。下图中进行了4次随机采样，得到了4个随机样本 $x_1,x_2,x_3,x_4$ ，并且得到了4个样本的 $f(x_i)$ 值，对于4个样本每一个得到的面积估算值相加取平均值，就完成了蒙特卡洛积分。

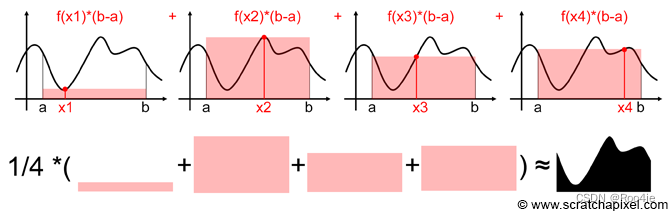
在这里插入图片描述

上述过程转换成数学公式如下:
$S=\frac{1}{4}[f(x_1)(b-a)+(f(x_2)(b-a))+f(x_3)(b-a)+f(x_4)(b-a)]\\ =\frac{1}{4}(b-a)[f(x_1)+f(x_2)+f(x_3)+f(x_4)]\\ =\frac{1}{4}(b-a)\sum^4_{i=1}f(x_i) \tag{2.2}$
对于一般情况下，假设积分函数为式(2.3)，但是被积函数 $g (x)$ 的原函数很难求出:
$I=\int^b_a g(x)dx \tag{2.3}$
其中被积函数 $g (x)$ 在区间 $[a, b]$ 内可积，如果选择一个概率密度函数为 $f_X(x)$ 的方式进行抽样，并且满足 $\int^b_af_X(x)dx=1$ ，那么令
$g^*(x)=\frac{g(x)}{f_X(x)} \tag{2.4}$

原有的积分可以写成如下形式:

$I=\int^b_a g^*(x)f_X(x)dx \tag{2.5}$
那么对于一般情况下求积分的步骤：

产生服从分不律 $F_x$ 的随机变量 $X_i(i=1,2,3,...,N)$ ；
计算均值
$\bar{I}=\frac{1}{N}\sum^N_{i=1}g^*(X_i) \tag{2.6}$

此时有 $\bar{I}=I$ 。

实际应用中一般取 $F_X$ 为均匀分布:
$f_X(x)=\frac{1}{b-a},a \leq x \leq b \tag{2.7}$
此时:
$g^*(x)=(b-a)g(x) \tag{2.8}$
代入积分表达式(2.5)有:
$I=\frac{(b-a)}{N}\int^b_ag(x)dx \tag{2.9}$
直观理解(2.8)式，在 $[a, b]$ 区间上按均匀分布取 $N$ 个随机样本 $X_i$ ，计算 $g(X_i)$ 并取均值，得到的相当于曲线阴影部分的 $Y$ 坐标平均值，然后乘以 $(b - a)$ 为 $X$ 坐标长度，得到的即为估计的阴影部分的面积，即最终的积分值。

再举个例子，设函数 $g(x)=3x^2$ ，计算其在区间[a, b]上的积分值，如下图所示，容易得到：
$G(x)=\int^b_a g(x)=x^3|^b_a$

在这里插入图片描述

假定要求的积分区间是[1, 3]，那么积分结果即为 $3^3-1^3=26$ 。
如果采用蒙特卡洛方法来计算函数积分，选择在区间 $[a, b]$ 上均匀分布概率密度函数 $f (x)$ ，那么由公式(2.8)可得：
$g^*(x) =g(x)(b-a)$
代入(2.6)式，同样可以得到下式：
$I=\frac{b-a}{N}\sum^n_{k=1}g(x_k)$
其中 $N$ 表示在区间 $[a, b]$ 上采样点的数量， $g(x_k)$ 为对应的在采样点 $x_k$ 处的函数值， $\in \{1,2,...,N\}$ 。如果采样点只有一个点如 ${2\}$ ，那么 $I_1=\frac{3-1}{1}×(3×2^2)=24$ ，如果采集点为 ${1,2,3\}$ ，那么结果 $I_3=\frac{3-1}{3}×(3×1^2+3×2^2+3×3^2)=28$ ，如果采样点为 ${1.0，1.25，1.5，1.75，2，2.25，2.5，2.75，3.0}$ ，那么计算结果为 $I_9=26.5$ 。如果不断的进行随机采样，获取更多的采样点，那么最终的结果是会不断的逼近26，最终利用python程序模拟采样过程，最终max=26.12198，min=25.8266:

import random
import time

# 曲线函数
def f(x):
    return 3 * x * x

def MonteCarloIntegral():
    '''
    每次采样10000个点，整个采集实验执行1000次，
    记录每次实验的结果，得到1000次实验中的最大值和最小值
    :return:
    '''
    run_times = 1000
    min_sum = 100000.0
    max_sum = -100000.0
    while run_times > 0:
        seed = int(time.time())
        num_samples = 10000 # 采样点数量
        # 采样空间
        a = 1.0
        b = 3.0
        sum = 0.0
        random.seed(seed)

        for i in range(num_samples):
            sample = random.uniform(a, b) #　均匀采样
            sum += (b - a) * f(sample)

        sum /= num_samples
        min_sum = min(min_sum, sum)
        max_sum = max(max_sum, sum)
        run_times -= 1

    print(min_sum, max_sum)

if __name__ == "__main__":
    MonteCarloIntegral()

2.4 离散空间采样和连续空间采样

利用蒙特卡罗积分的方式能够计算积分，但是上面提到的都是在已知概率密度函数(PDF)的前提下采集很多样本进行蒙特卡罗积分，但是并没有提到如何根据分布生成样本的过程，这涉及到采样方法的问题，在已知PDF的前提下如何进行采样以及采样得到的数据就是服从PDF的分布。

先考虑在离散空间的采样方式，假设有一个离散空间，其样本的取值有4个值分布用 $x_i$ 表示，并且4个值对应的概率值同样已知用 $P_i$ 表示，要生成符合下图所示分布的样本，首先将表示概率的直方图堆叠起来，即如下图有图所示，然后生成一系列均匀分布的采样点，该采样点对应的值在哪个区间内，就返回对应的值。

在这里插入图片描述

具体代码实现:

import random
import matplotlib.pyplot as plt

def sampling_in_discrete_space():
    # 采样
    num = [0, 0, 0, 0]
    for i in range(100):
        value = random.random()
        if value >= 0 and value < 0.3:
            num[0] += 1
        elif value < 0.7:
            num[1] += 1
        elif value < 0.8:
            num[2] += 1
        else:
            num[3] += 1

    print(f"采样结果: {num}")

    x = [1, 2, 3, 4]
    # 使用text显示数值
    for a, b in zip(x, num):
        plt.text(a, b + 0.05, '%.0f' % b, ha='center', va='bottom', fontsize=11)
    plt.bar(x, num, color=['b', 'orange', 'g', 'r'])
    plt.xticks(x, ['x1', 'x2', 'x3', 'x4'])
    plt.show()

if __name__ == '__main__':
    sampling_in_discrete_space()

在这里插入图片描述

可以看到采集100个点的最终结果跟上图中的概率分布是一样的结果。

对于连续空间的采样，可以类似离散空间采样的方法，将每一个取值的概率看成极限细的直方图，如下图所示：
在这里插入图片描述

左边是其概率密度函数PDF，右边是其累积分布函数CDF。具体的采样方法和离散空间类似：首先生成在[0,1]均匀分布的随机数（对应于右图的y轴），在右图CDF曲线上寻找该y值所对应的x值（即采样点）。反映到数学关系上即为：
$y=F_X(x)\\ x=F^{-1}_x(y)$
其中y服从[0,1]的均匀分布，x是最终得到的服从 $p (x)$ 的采样点。该方法适用于累积分布函数CDF可求解其逆函数的情况，若无法求解CDF的逆函数，则可采用拒绝采样方法。

举个例子，利用指数分布函数，采集1000个服从指数分布的样本，指数分布表达式如下:
$\begin{cases} e^{-x},\quad x\geq 0 \\[2ex] 0, \quad \quad x<0 \end{cases}$
由概率密度函数可以求得，该随机变量所对应的累积分布函数(CDF)为:
$F(x)=\int^x_{-\infty}f(x)dx=\int^x_{-\infty} e^{-x} dx=1-e^{-x}$
羡慕求解逆函数:
$F(F^{-1}(x))=1-e^{-F^{-1}(x)}=x\\ 1-x=e^{-F^{-1}(x)}\\ ln(1-x)=-F^{-1}(x)\\ F^{-1}(x)=-ln(1-x)$
有了逆函数，就可以通过采样均匀分布的点，将其代入到上述公式，进的得到服从指数分布的样本点。

import random
import math
import matplotlib.pyplot as plt
import numpy as np

def inverse_transform_sampling():
    sample_points = []
    for i in range(1000):
        num = random.random()
        sample_points.append(-math.log(1 - num))

    return sample_points

def plot_sampling(sample_points):
    # 绘制采样点
    n, bins, patches = plt.hist(sample_points, bins=100, density=True)
    # 绘制概率密度函数
    x = np.linspace(0, 10, 100)
    y = np.exp(-x)
    plt.plot(x, y)
    plt.legend(['real PDF', 'sample hist'])
    plt.show()

if __name__ == '__main__':
    sample_points = inverse_transform_sampling()
    plot_sampling(sample_points)

最终结果可以发现是跟指数分布的结果是一致的：

在这里插入图片描述

2.4 NeRF中的采样策略

参考链接:https://zhuanlan.zhihu.com/p/532937226

NeRF的采样策略是先进行分层采样再进行重要性采样，分层随机抽样是利用一个或多个变量把总体划分成若干个子总体，每个个体属于且仅属于一个子总体，在每个子总体中独立地进行简单随机抽样，再把所有子总体中抽取的样本合在一起作为总样本。

第1次采样：在相机射线上，由 near 和 far 构成的范围 n 等分，然后在每个小区间内均匀采样得到一个采样点 $C_i$ ，最终一共 n 个采样点。将采样点的位置信息和视角信息的PE编码信息输入 MLP，MLP 输出每个采样点的 Volume Density。

第2次采样：第2次采样是基于第一次采样点的结果。采样点 $c_i$ 会有个权重 $weight_i$ 。那么，第二次采样会对第一次采样结果中 $weight_i$ 较大的区域多采样，在 $weight_i$ 值小的地方采样少一些。
在这里插入图片描述

对于第1次采样: 在区间 $[a, b]$ 之间均匀采样 $N^c$ 个点 $d_{coarse}$ ，将得到的采样点的位置信息和其他信息输入 MLP，MLP 输出每个采样点的体密度 $\sigma$ 。注意，用大写的 $C_i$ 代表第 $i$ 个采样点。而小写的 $c_i$ 代表它的RGB颜色向量。
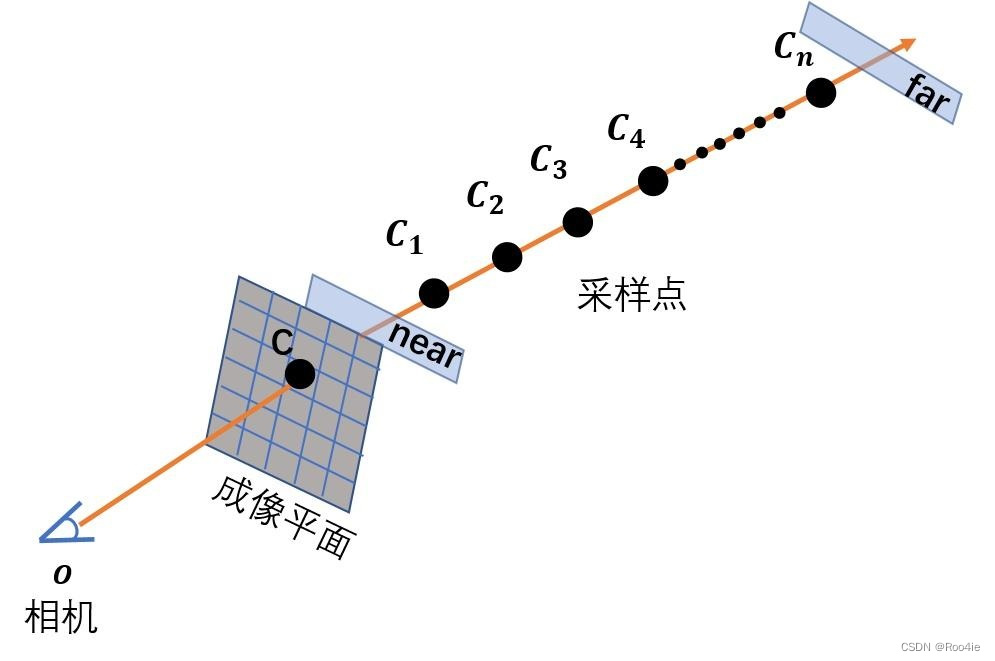
在这里插入图片描述

再进行第2次采样之前需要计算几个关键值，首先是透明度 $a$ ，可以由**体密度 $\sigma$ **和两个采样点之间的距离 $\delta$ 计算得到:
$a=(1-e^{-\sigma_i\delta_i}) \tag{2.10}$
如上式两个采样点之间的距离 $\delta$ 通常是已知的，当体密度 $\sigma=0$ 时，透明度 $a = 0$ ，即在相机发出的光吉许向后传播时，当前点对成像点的颜色是无共享的，也不影响后面点对成像点颜色的贡献；当体密度 $\sigma \rightarrow 0$ 时，透明度 $\rightarrow 0$ ，此时物体完全不透明，使得从相机发出的光被完全阻挡在当前点，使得当前点后面的点对成像点 C 的颜色无贡献。由上面可以得到成像点 $C$ 的颜色公式:
$\hat{C}=c_1a_1+\{c_2a_2[(1-a_1)]\}+\{c_3a_3[(1-a_1)(1-a_2)]\}+...+\{c_na_n[(1-a_1)(1-a_2)...(1-a_{n-1})]\} \tag{2.11}$
其中 $a_i$ 表示的就是透明度，而 $1-a_1)(1-a_2)...(1-a_{i-1})$ 就是对应采样点 $C_i$ 的透过率 $T_i$ ，代入2.10对应公式可以写为：
$T_i=(1-a_1)(1-a_2)...(1-a_{i-1})=e^{-\sigma_1\delta_1}×e^{-\sigma_2\delta_2}×...×e^{-\sigma_1\delta_1}= e^{-\sum^{i-1}_{j=1}\sigma_j\delta_j} \tag{2.12}$
那么2.11可以化简成：
$\hat{C} = c_1a_1 + c_2a_2T_2+c_3a_3T_3+...+c_ia_iT_i=\sum^N_{i=1}c_ia_iT_i \tag{2.13}$
将式(2.10)代入(2.12)可得:
$\hat{C}=\sum^N_{i=1}c_i(1-e^{-\sigma_i\delta_i})T_i \tag{2.13}$
$T_i$ 可以理解为除去当前点 $C_i$ ，前面的点 $C_1,C_2,...,C_{i-1}$ 对成像点 $C$ 的颜色的影响。透明度 $a_i$ 乘上 $T_i$ 的乘积才是最终的 $C_i$ 对成像点C的颜色的权重 $weight_i$ ，记做 $w_i=a_iT_i$ , $\hat{C}$ 表示用MLP网络预测得到的成像点 C 的颜色。

对于第2次采样：根据第一次采样点 $C_i$ ，以及计算得到的权重值 $w_i$ 计算可得下式:
$\hat{C}_{c(r)}=\sum^{N_c}_{i=1}w_i c_i \\ \tag{2.14}$
这里的权重 $w_i$ 是通过体密度 $\sigma$ (coarse MLP网络输出)，两个采样点之间的距离 $\delta$ (第一次均匀采样)，透过率 $T_i$ (transmittance)，计算得到：
$w_i=T_i(1-e^{-\sigma_i\delta_i}) \tag{2.11}$
其中权重需要进行归一化：
$\hat{w_i}=\frac{w_i}{\sum^{N_c}_{j=1}w_j}$
这里面的权重 $\hat{w}_i$ 可以看成沿着射线的分段常数概率密度函数 (Piecewise-constant PDF)，利用权重 $\hat{w}_i$ 也即PDF可以构造累积分布函数CDF，通过这个概率密度函数可以粗略地得到射线上物体的分布情况。

在这里插入图片描述

举个例子，

1）第1次采样根据均匀分布得到10个点及其对应的权重(这里为了简单方便随机生成10个点的权重 )，然后利用归一化权重的获得概率密度函数(PDF)，根据概率密度函数(PDF)计算累积分布函数(CDF)；

2）累积分布函数(CDF)的范围是[0,1], 再在[0,1]之间均匀采集100个点，其中 $d_{fine}=CDF^{-1}(d_{seed}), d_{seed} \sim U[0,1]$ ， $CDF^{-1}$ 表示的是累积分布函数的反函数，通过反函数计算得到第二次采样点 $d_{fine}$ ，该方式跟蒙特卡洛积分中的逆采样方式是一样的；

3）然后再判断100个点在给定10个点的累积分布函数中对应的位置；

4）再根据累积分布函数插值计算offset，再对应的原点上插值。

上述过程的代码实现：

import numpy as np
import matplotlib.pyplot as plt

# 原始数据集中的粗采样点，从3.01到4.0，以0.1为间隔进行均匀采样。
d_coarse = np.arange(3.01, 4.01, 0.1)
# 随机生成10个点的权重
w = np.array([0, 0.3, 0.9, 0.9, 0.6, 0.6, 0.9, 0.9, 0.3, 0])
# 权重归一化
w = w / np.sum(w)  # pdf
# 计算权重累积和，用于构建累积分布函数
# np.cumsum()返回一个与原始数组大小相同的新数组，
# 其中的每个元素都是原数组中对应位置之前所有元素的和。
# arr = np.array([1, 2, 3, 4, 5])
# cumulative_sum = np.cumsum(arr)
# 原始数组 arr 的累积和被计算为 [1, 1+2, 1+2+3, 1+2+3+4, 1+2+3+4+5]
w_sum = np.cumsum(w)  # cdf

#  d_fine 用于在新数据集上进行采样，从0.00001到1，以0.01为间隔，
#  也可以采用下面生成随机数的方式
d_seed = np.arange(0.00001, 1.01, 0.01)
# d_seed = np.random.randn(100)
# d_seed = d_seed - np.mean(d_seed)
# d_seed = d_seed / np.max(d_seed)
w_corr = []  # 用于可视化的权重修正数组
d_fine = []  # 存储新数据集的数据点
# 判断这100个点在给定10个点的cdf中对应的位置
for i in range(len(d_seed)):
    v = d_seed[i]
    for j in range(len(w_sum) - 1):
        k = j + 1
        # 寻找w_sum中的相邻区间，使得v介于这两个区间之间
        if v >= w_sum[j] and v <= w_sum[k]:
            # 计算修正的权重 w_corr，
            # 以及在原始数据点之间插值得到的新数据点 d_fine。
            w_corr.append(w_sum[k] - w_sum[j])
            offset1 = (v - w_sum[j]) / (w_sum[k] - w_sum[j])
            bias = offset1 * (d_coarse[k] - d_coarse[j])
            #　将这些值添加到新数据集
            d_fine.append(0.5 * (d_coarse[k] + d_coarse[j]) + bias)
            break

# Plotting
plt.figure(1)
plt.plot(d_coarse, w)
plt.scatter(d_fine, w_corr)
plt.axis([3, 4, 0, 0.2])
plt.xlabel("positions d")
plt.ylabel("normalized-weight w")
plt.legend(["origin 10 pts", "new 100 pts"])
plt.show()

最终结果：
在这里插入图片描述

2.5 拒绝采样

如果无法对累积分布函数求逆，那么自然就无法使用逆变换的方法进行采样，此时我们考虑另一种采样方式：拒绝采样法。拒绝法采样的原理非常简单，如果我们难以直接在一个空间A均匀采样，那么我们可以考虑在一个更大的空间B内均匀采样，然后判断采样点是否在空间A中，如果在，则接受该采样点；否则拒绝该采样点。具体如下图所示，已知概率密度函数为 $f (x)$ 即图中的曲线所示，利用一条比原曲线都大的直线Max与x轴区间 $[A, B]$ ，将整个曲线包裹起来，此时只需要在x轴 $[A, B]$ 范围内，y轴 $[0, M a x]$ 范围内进行均匀采样，如果y轴方向满足 $y < f (x)$ 那么就保留 $x$ ，反之则拒绝 $x$ ，即实现保留在 $f (x)$ 范围内的值，而拒绝其他值。

在这里插入图片描述

代码实现:

import random
import matplotlib.pyplot as plt
import numpy as np

def rejection_sampling(A, B, Max, nums):
    sample_points = []
    for i in range(nums):
        x = random.uniform(A, B)
        y = random.uniform(0, Max)
        sample_points.append((x, y))

    correct_points = []
    for i in range(len(sample_points)):
        if sample_points[i][1] < f(sample_points[i][0]):
            correct_points.append(sample_points[i])

    return sample_points, correct_points, (A, B, Max)

def get_x_y_from_points(points):
    x = [p[0] for p in points]
    y = [p[1] for p in points]
    return x, y

def f(x):
    return -2 * (x - 1) ** 2 + 2

def plot_results(sample_points, correct_points, params):
    A, B, Max = params

    plt.subplot(1, 2, 1)
    # 绘制f(x)
    x = np.linspace(A, B, 1000)
    y = [f(x[i]) for i in range(len(x))]
    plt.plot(x, y)

    # 绘制矩形框
    plt.axhline(0, color='black')
    plt.axhline(Max, color='black')
    plt.axvline(A, color='black')
    plt.axvline(B, color='black')
    plt.plot()

    # 绘制采样点
    x1, y1 = get_x_y_from_points(sample_points)
    x2, y2 = get_x_y_from_points(correct_points)
    plt.scatter(x1, y1, s=5)
    plt.scatter(x2, y2, s=5)

    # 绘制直方图
    plt.subplot(1, 2, 2)
    n, bins, patches = plt.hist(x2, bins=100, density=True)

    plt.show()

if __name__ == '__main__':
    A, B, Max = 0, 2, 3
    nums = 1000
    sample_points, correct_points, params = rejection_sampling(A, B, Max, nums)
    plot_results(sample_points, correct_points, params)

在这里插入图片描述

Roo4ie

关注

4
点赞
踩
11

收藏

觉得还不错? 一键收藏
1
评论
NeRF理解-- Nerf采样策略

具体如下图所示，已知概率密度函数为。利用蒙特卡罗积分的方式能够计算积分，但是上面提到的都是在已知概率密度函数(PDF)的前提下采集很多样本进行蒙特卡罗积分，但是并没有提到如何根据分布生成样本的过程，这涉及到采样方法的问题，举个例子，一颗6面的骰子，有1，2，3，4，5，6这6个取值，每个取值取到的概率都为1/6。表示，要生成符合下图所示分布的样本，首先将表示概率的直方图堆叠起来，即如下图有图所示，然后生成一系列均匀分布的采样点，该采样点对应的值在哪个区间内，就返回对应的值。，最终一共 n 个采样点。
复制链接

扫一扫