前言
如果没有笛卡尔平面直角坐标系,那么涉及平面向量的问题只能用基向量的方法[形的角度]求解,不能用代数方法[数的角度]计算;同理如果没有空间直角坐标系的介入,立体几何中的问题也就只能从形的角度思考,而不能用代数方法[数的角度]来计算;所以建系的目的主要是想把有关形的问题,通过代数的方法计算解决;
本博文旨在总结立体几何中常见几何体的建系方法和类型,比如正四面体中、正三棱柱中、四棱锥等中的建系方法,坐标计算方法等,便于学习。而且我们应该知道,当建立的坐标系不同时,计算的难度是不一样的。
建平直系
- 平面问题中若涉及平面向量的计算问题,常可以建立平面直角坐标系;
【2017河北武邑中学一模,文11】在 R t △ A B C Rt\triangle ABC Rt△ABC中, C A = C B = 3 CA=CB=3 CA=CB=3, M M M, N N N是斜边 A B AB AB上的两个动点, M N MN MN = = = 2 \sqrt{2} 2,则 C M → ⋅ C N → \overrightarrow{CM}\cdot \overrightarrow{CN} CM⋅CN的取值范围是【】
分析:求向量的内积的取值范围,应该想到用内积的坐标运算,本题目难点是一般想不到主动建系,由形的运算转化为数的运算。
解:如图所示,以点 C C C为坐标原点,分别以 C B 、 C A CB、CA CB、CA所在的直线为 x 、 y x、y x、y轴建立如同所示的坐标系,则 C ( 0 , 0 ) C(0,0) C(0,0), A ( 0 , 3 ) A(0,3) A(0,3), B ( 3 , 0 ) B(3 ,0) B(3,0),设点 N N N的横坐标为 x x x,则由等腰直角三角形可知,点 N N N的纵坐标为 3 − x 3-x 3−x,即点 N ( x , 3 − x ) N(x,3-x) N(x,3−x),

又由 M N = 2 MN=\sqrt{2} MN=2,计算可知点 M ( x − 1 , 4 − x ) M(x-1,4-x) M(x−1,4−x),则 C M → = ( x − 1 , 4 − x ) \overrightarrow{CM}=(x-1,4-x) CM=(x−1,4−x), C N → = ( x , 3 − x ) \overrightarrow{CN}=(x,3-x) CN=(x,3−x),
由于点 M , N M,N M,N是动点,取两个极限位置研究 x x x的取值范围,
当点 M M M位于点 A A A时, x x x取到最小值 1 1 1,当点 N N N位于点 B B B时, x x x取到最大值 3 3 3,即 1 ≤ x ≤ 3 1\leq x\leq 3 1≤x≤3,
则 C M → ⋅ C N → = f ( x ) = ( x − 1 , 4 − x ) ⋅ ( x , 3 − x ) \overrightarrow{CM}\cdot \overrightarrow{CN}=f(x)=(x-1,4-x)\cdot (x,3-x) CM⋅CN=f(x)=(x−1,4−x)⋅(x,3−x)
= x ( x − 1 ) + ( 4 − x ) ( 3 − x ) = 2 ( x − 2 ) 2 + 4 =x(x-1)+(4-x)(3-x)=2(x-2)^2+4 =x(x−1)+(4−x)(3−x)=2(x−2)2+4, x ∈ [ 1 , 3 ] x\in [1,3] x∈[1,3]
当 x = 2 x=2 x=2时, f ( x ) m i n = f ( 2 ) = 4 f(x)_{min}=f(2)=4 f(x)min=f(2)=4,当 x = 1 x=1 x=1或 x = 3 x=3 x=3时, f ( x ) m a x = f ( 1 ) = f ( 3 ) = 6 f(x)_{max}=f(1)=f(3)=6 f(x)max=f(1)=f(3)=6,
即 f ( x ) ∈ [ 4 , 6 ] f(x)\in [4,6] f(x)∈[4,6]。故选 D D D。
【解后反思】对于以图形为背景的向量数量积运算的题目,只需把握图形的特征,建立适当的平面直角坐标系,写出相应点的坐标即可求解。
【2019届高三理科数学三轮模拟试题】如图,已知两点 A A A, B B B在单位圆上, ∠ y O B = 6 0 ∘ \angle yOB=60^{\circ} ∠yOB=60∘, ∠ x O A = 3 0 ∘ \angle xOA=30^{\circ} ∠xOA=30∘,则 ∣ 2 O A → + 3 O B → ∣ |2\overrightarrow{OA}+3\overrightarrow{OB}| ∣2OA+3OB∣=___________。

法1:向量法,由题目可知, ∠ A O B = 12 0 ∘ \angle AOB=120^{\circ} ∠AOB=120∘, ∣ O A → ∣ = ∣ O B → ∣ = 1 |\overrightarrow{OA}|=|\overrightarrow{OB}|=1 ∣OA∣=∣OB∣=1,
则 ∣ 2 O A → + 3 O B → ∣ = ∣ 2 O A → + 3 O B → ∣ 2 |2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{|2\overrightarrow{OA}+3\overrightarrow{OB}|^2} ∣2OA+3OB∣=∣2OA+3OB∣2
= 4 ∣ O A → ∣ 2 + 9 ∣ O B → ∣ 2 + 2 × 2 × 3 × O A → ⋅ O B → =\sqrt{4|\overrightarrow{OA}|^2+9|\overrightarrow{OB}|^2+2\times 2\times 3\times \overrightarrow{OA}\cdot \overrightarrow{OB}} =4∣OA∣2+9∣OB∣2+2×2×3×OA⋅OB
= 4 + 9 + 2 × 2 × 3 × 1 × 1 × ( − 1 2 ) = 7 =\sqrt{4+9+2\times 2\times 3\times 1\times 1\times (-\cfrac{1}{2})}=7 =4+9+2×2×3×1×1×(−21)=7,故 ∣ 2 O A → + 3 O B → ∣ = 7 |2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7} ∣2OA+3OB∣=7。
法2:坐标法,已知 A ( 3 2 , 1 2 ) A(\cfrac{\sqrt{3}}{2},\cfrac{1}{2}) A(23,21), B ( − 3 2 , 1 2 ) B(-\cfrac{\sqrt{3}}{2},\cfrac{1}{2}) B(−23,21),则 O A → = ( 3 2 , 1 2 ) \overrightarrow{OA}=(\cfrac{\sqrt{3}}{2},\cfrac{1}{2}) OA=(23,21),
O B → = ( − 3 2 , 1 2 ) \overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2},\cfrac{1}{2}) OB=(−23,21),则 2 O A → + 3 O B → = ( − 3 2 , 5 2 ) 2\overrightarrow{OA}+3\overrightarrow{OB}=(-\cfrac{\sqrt{3}}{2},\cfrac{5}{2}) 2OA+3OB=(−23,25),
故 ∣ 2 O A → + 3 O B → ∣ = ( − 3 2 ) 2 + ( 5 2 ) 2 = 7 |2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{(-\cfrac{\sqrt{3}}{2})^2+(\cfrac{5}{2})^2}=\sqrt{7} ∣2OA+3OB∣=(−23)2+(25)2=7。
法3:解三角形法,由向量的平行四边形法则可知,所求的模长即 △ O C D \triangle OCD △OCD中的边长 ∣ O C ∣ |OC| ∣OC∣,由已知 ∣ O D ∣ = 3 ∣ O B ∣ = 3 |OD|=3|OB|=3 ∣OD∣=3∣OB∣=3, ∣ C D ∣ = 2 ∣ O A ∣ = 2 |CD|=2|OA|=2 ∣CD∣=2∣OA∣=2, ∠ O D C = 6 0 ∘ \angle ODC=60^{\circ} ∠ODC=60∘,

由余弦定理可知 ∣ 2 O A → + 3 O B → ∣ 2 = ∣ O C ∣ 2 = 2 2 + 3 2 − 2 × 2 × 3 × c o s 6 0 ∘ = 7 |2\overrightarrow{OA}+3\overrightarrow{OB}|^2=|OC|^2=2^2+3^2-2\times2\times 3\times cos60^{\circ}=7 ∣2OA+3OB∣2=∣OC∣2=22+32−2×2×3×cos60∘=7,
故 ∣ 2 O A → + 3 O B → ∣ = 7 |2\overrightarrow{OA}+3\overrightarrow{OB}|=\sqrt{7} ∣2OA+3OB∣=7。
【2019届高三理科数学二轮用题】在矩形 A B C D ABCD ABCD中, A B = 2 AB=2 AB=2, A D = 4 AD=4 AD=4, A C AC AC与 B D BD BD相交于点 O O O,过点 A A A作 A E ⊥ B D AE\perp BD AE⊥BD于 E E E,则 A E → ⋅ A C → \overrightarrow{AE}\cdot \overrightarrow{AC} AE⋅AC=【】
法1:从形的角度思考,采用坐标法求解;以点 A A A为坐标原点建立如图所示的直角坐标系,
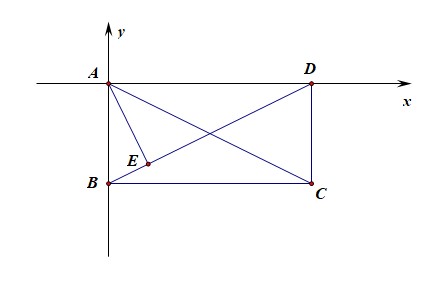
则可知 A ( 0 , 0 ) A(0,0) A(0,0), B ( 0 , − 2 ) B(0,-2) B(0,−2), C ( 4 , − 2 ) C(4,-2) C(4,−2), D ( 4 , 0 ) D(4,0) D(4,0),设 E ( x , y ) E(x,y) E(x,y),
则由 k A E ⋅ k B D = − 1 k_{AE}\cdot k_{BD}=-1 kAE⋅kBD=−1,可得 y = − 2 x y=-2x y=−2x①,又直线 B D : 2 y = x − 4 BD:2y=x-4 BD:2y=x−4②,
联立①②可得, x = 4 5 x=\cfrac{4}{5} x=54, y = − 8 5 y=-\cfrac{8}{5} y=−58,
则 A E → ⋅ A C → = ( 4 5 , − 8 5 ) ⋅ ( 4 , − 2 ) = 32 5 \overrightarrow{AE}\cdot \overrightarrow{AC}=(\cfrac{4}{5},-\cfrac{8}{5})\cdot (4,-2)=\cfrac{32}{5} AE⋅AC=(54,−58)⋅(4,−2)=532,故选 C C C.
法2:本题目是否还可以用基向量法,以 A B → \overrightarrow{AB} AB和 A D → \overrightarrow{AD} AD为基向量来表示其他向量,待思考;
建空间系
- 正四面体中的建系,建立空间直角坐标系;
如图,正四面体 P − A B C P-ABC P−ABC中, D D D、 E E E分别是 A B AB AB和 P C PC PC的中点,则直线 A E AE AE与 P D PD PD所成角的余弦值是多少?
法1:空间向量法,如图所示, P F ⊥ PF\perp PF⊥面 A B C ABC ABC, F F F为 Δ A B C \Delta ABC ΔABC的中心,
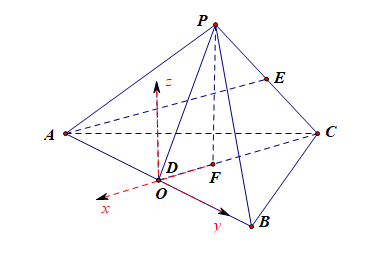
以点 D D D为坐标原点,以 D F DF DF、 D B DB DB以及与 F P FP FP平行的直线分别为 x x x, y y y, z z z轴建立如图所示的空间直角坐标系,
令正四面体的棱长为 2 2 2,则得到以下点的空间坐标
D ( 0 , 0 , 0 ) D(0,0,0) D(0,0,0), A ( 0 , − 1 , 0 ) A(0,-1,0) A(0,−1,0), B ( 0 , 1 , 0 ) B(0,1,0) B(0,1,0),
C ( − 3 , 0 , 0 ) C(-\sqrt{3},0,0) C(−3,0,0), P ( − 3 3 , 0 , 2 6 3 ) P(-\cfrac{\sqrt{3}}{3},0,\cfrac{2\sqrt{6}}{3}) P(−33,0,326), E ( − 2 3 3 , 0 , 6 3 ) E(-\cfrac{2\sqrt{3}}{3},0,\cfrac{\sqrt{6}}{3}) E(−323,0,36),
则有 P D → = ( 3 3 , 0 , − 2 6 3 ) \overrightarrow{PD}=(\cfrac{\sqrt{3}}{3},0,-\cfrac{2\sqrt{6}}{3}) PD=(33,0,−326); A E → = ( − 2 3 3 , 1 , 6 3 ) \overrightarrow{AE}=(-\cfrac{2\sqrt{3}}{3},1,\cfrac{\sqrt{6}}{3}) AE=(−323,1,36);
令异面直线 P D PD PD和 A E AE AE的夹角为 θ \theta θ,则有 c o s θ cos\theta cosθ
= ∣ 3 3 ⋅ ( − 2 3 3 ) + 0 ⋅ 1 + ( − 2 6 3 ⋅ 6 3 ) ∣ ( 3 3 ) 2 + ( − 2 6 3 ) 2 ⋅ ( − 2 3 3 ) 2 + 1 2 + ( 6 3 ) 2 = 2 3 =\cfrac{|\cfrac{\sqrt{3}}{3}\cdot (-\cfrac{2\sqrt{3}}{3})+0\cdot 1+(-\cfrac{2\sqrt{6}}{3}\cdot \cfrac{\sqrt{6}}{3})|}{\sqrt{(\cfrac{\sqrt{3}}{3})^2+(-\cfrac{2\sqrt{6}}{3})^2}\cdot \sqrt{(-\cfrac{2\sqrt{3}}{3})^2+1^2+(\cfrac{\sqrt{6}}{3})^2}}=\cfrac{2}{3} =(33)2+(−326)2⋅(−323)2+12+(36)2∣33⋅(−323)+0⋅1+(−326⋅36)∣=32。
说明:向量的夹角范围为 [ 0 , π ] [0,\pi] [0,π],两异面直线的夹角范围 [ 0 , π 2 ] [0,\cfrac{\pi}{2}] [0,2π]。
法2:立体几何法,先作再证后算。
思路:异面直线所成的角,一般是经过平移,使其相交,构建三角形来计算。

过点 A A A做 A M / / B C AM//BC AM//BC,过点 B B B做 B M / / A C BM//AC BM//AC交 A M AM AM于点 M M M,
点 F F F、 H H H、 G G G分别是线段 P B PB PB、 A M AM AM、 B D BD BD的中点,连接 H F HF HF、 F G FG FG、 H G HG HG,
则有 E F = / / A H EF\;\;{}_{=}^{//}AH EF=//AH,则 A E / / F H AE//FH AE//FH,又 P D / / F G PD//FG PD//FG,故 ∠ H F G \angle HFG ∠HFG为两条异面直线所成的角。
设正四面体的棱长为 2 2 2,则 A E = F H = P D = 3 AE=FH=PD=\sqrt{3} AE=FH=PD=3, F G = 3 2 FG=\cfrac{\sqrt{3}}{2} FG=23;
又在 Δ A H G \Delta AHG ΔAHG中, A H = 1 AH=1 AH=1, A G = 3 2 AG=\cfrac{3}{2} AG=23, ∠ H A G = 6 0 ∘ \angle HAG=60^\circ ∠HAG=60∘,
由余弦定理可知, H G = 7 2 HG=\cfrac{\sqrt{7}}{2} HG=27,
在 Δ H F G \Delta HFG ΔHFG中, H F = 3 HF=\sqrt{3} HF=3, F G = 3 2 FG=\cfrac{\sqrt{3}}{2} FG=23, H G = 7 2 HG=\cfrac{\sqrt{7}}{2} HG=27,
由余弦定理可知 c o s ∠ H F G = 2 3 cos\angle HFG=\cfrac{2}{3} cos∠HFG=32。
- 四棱锥中的建系,建立空间直角坐标系;
【四棱锥中的建系】【2017凤翔中学第三次月考理科第19题】如图所示,四棱锥 P − A B C D P-ABCD P−ABCD中,底面 A B C D ABCD ABCD是个边长为2的正方形,侧棱 P A ⊥ PA\perp PA⊥底面 A B C D ABCD ABCD,且 P A = 2 PA=2 PA=2, Q Q Q是 P A PA PA的中点.

(1)证明: B D ⊥ BD\perp BD⊥平面 P A C PAC PAC ;暂略
(2)求二面角 C − B D − Q C-BD-Q C−BD−Q的余弦值。
分析:有题可知, A B 、 A P 、 A D AB、AP、AD AB、AP、AD两两垂直,以 A A A为坐标原点,分别以 A B 、 A D 、 A P AB、AD、AP AB、AD、AP所在直线为 x , y , z x,y,z x,y,z轴建立空间直角坐标系,如图所示。
则点 B ( 2 , 0 , 0 ) B(2,0,0) B(2,0,0), C ( 2 , 2 , 0 ) C(2,2,0) C(2,2,0), D ( 0 , 2 , 0 ) D(0,2,0) D(0,2,0), Q ( 0 , 0 , 1 ) Q(0,0,1) Q(0,0,1),
所以 B D → = ( − 2 , 2 , 0 ) \overrightarrow{BD}=(-2,2,0) BD=(−2,2,0), B Q → = ( − 2 , 0 , 1 ) \overrightarrow{BQ}=(-2,0,1) BQ=(−2,0,1),
设平面 B D Q BDQ BDQ的法向量为 m ⃗ = ( x , y , z ) \vec{m}=(x,y,z) m=(x,y,z),则有
{ m ⃗ ⊥ B D → m ⃗ ⊥ B Q → \begin{cases}\vec{m}\perp\overrightarrow{BD}\\\vec{m}\perp\overrightarrow{BQ}\end{cases} {m⊥BDm⊥BQ ⟹ { m ⃗ ⋅ B D → = 0 m ⃗ ⋅ B Q → = 0 \Longrightarrow \begin{cases}\vec{m}\cdot\overrightarrow{BD}=0\\\vec{m}\cdot\overrightarrow{BQ}=0\end{cases} ⟹{m⋅BD=0m⋅BQ=0
即 { − 2 x + 2 y = 0 − 2 x + z = 0 \begin{cases}-2x+2y=0\\-2x+z=0\end{cases} {−2x+2y=0−2x+z=0,可以取 m ⃗ = ( 1 , 1 , 2 ) \vec{m}=(1,1,2) m=(1,1,2)
平面 B D C BDC BDC的法向量为 n ⃗ = ( 0 , 0 , 1 ) \vec{n}=(0,0,1) n=(0,0,1),
设二面角 C − B D − Q C-BD-Q C−BD−Q为 θ \theta θ,由图可知, θ \theta θ为钝角,则有
c o s θ = − ∣ c o s < m ⃗ , n ⃗ > ∣ = − m ⃗ ⋅ n ⃗ ∣ m ⃗ ∣ ∣ n ⃗ ∣ = − 2 6 = − 6 3 cos\theta=-|cos<\vec{m},\vec{n}>|=-\cfrac{\vec{m}\cdot\vec{n}}{|\vec{m}||\vec{n}|}=-\cfrac{2}{\sqrt{6}}=-\cfrac{\sqrt{6}}{3} cosθ=−∣cos<m,n>∣=−∣m∣∣n∣m⋅n=−62=−36
所以二面角 C − B D − Q C-BD-Q C−BD−Q的余弦值为 − 6 3 -\cfrac{\sqrt{6}}{3} −36。
- 正三棱柱中的建系,建立空间直角坐标系;
【正三棱柱中的建系】【2019届宝鸡市高三理科数学质检Ⅰ第10题】已知正三棱柱 A B C − A 1 B 1 C 1 ABC-A_1B_1C_1 ABC−A1B1C1中, A B = A A 1 = 2 AB=AA_1=2 AB=AA1=2,则异面直线 A B 1 AB_1 AB1与 C A 1 CA_1 CA1所成角的余弦值为【】
【法1】空间向量法,第一种建系方式;以点 A A A为坐标原点,以 A C AC AC, A A 1 AA_1 AA1分别为 y y y、 z z z轴,以和 A C AC AC垂直的直线为 x x x轴,建立如图所示的空间直角坐标系,
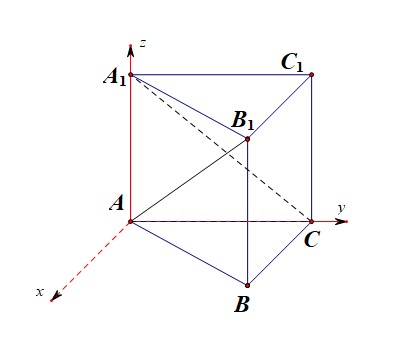
则 A ( 0 , 0 , 0 ) A(0,0,0) A(0,0,0), B ( 3 , 1 , 0 ) B(\sqrt{3},1,0) B(3,1,0), A 1 ( 0 , 0 , 2 ) A_1(0,0,2) A1(0,0,2), B 1 ( 3 , 1 , 2 ) B_1(\sqrt{3},1,2) B1(3,1,2), C ( 0 , 2 , 0 ) C(0,2,0) C(0,2,0),
A B 1 → = ( 3 , 1 , 2 ) \overrightarrow{AB_1}=(\sqrt{3},1,2) AB1=(3,1,2), A 1 C → = ( 0 , 2 , − 2 ) \overrightarrow{A_1C}=(0,2,-2) A1C=(0,2,−2),且线线角的范围是 [ 0 , π 2 ] [0,\cfrac{\pi}{2}] [0,2π],
故所求角的余弦值为 ∣ c o s < A B 1 → , A 1 C → > ∣ = ∣ 1 × 2 + 2 × ( − 2 ) ∣ 8 × 8 = 1 4 |cos<\overrightarrow{AB_1},\overrightarrow{A_1C}>|=\cfrac{|1\times 2+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4} ∣cos<AB1,A1C>∣=8×8∣1×2+2×(−2)∣=41。故选 C C C。
【法1】空间向量法,第二种建系方式;以 B N BN BN的中点为坐标原点建立如图所示的空间直角坐标系,
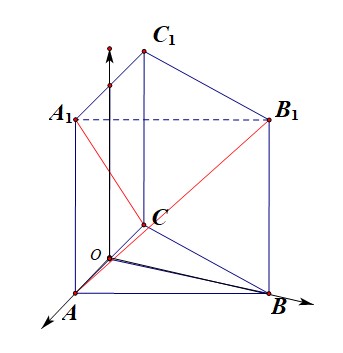
则 A ( 1 , 0 , 0 ) A(1,0,0) A(1,0,0), B ( 0 , 3 , 0 ) B(0,\sqrt{3},0) B(0,3,0), C ( − 1 , 0 , 0 ) C(-1,0,0) C(−1,0,0), A 1 ( 1 , 0 , 2 ) A_1(1,0,2) A1(1,0,2), B 1 ( 0 , 3 , 2 ) B_1(0,\sqrt{3},2) B1(0,3,2), C 1 ( − 1 , 0 , 2 ) C_1(-1,0,2) C1(−1,0,2),
A B 1 → = ( − 1 , 3 , 2 ) \overrightarrow{AB_1}=(-1,\sqrt{3},2) AB1=(−1,3,2), A 1 C → = ( − 2 , 0 , − 2 ) \overrightarrow{A_1C}=(-2,0,-2) A1C=(−2,0,−2),且线线角的范围是 [ 0 , π 2 ] [0,\cfrac{\pi}{2}] [0,2π],
故所求角的余弦值为 ∣ c o s < A B 1 → , A 1 C → > ∣ = ∣ − 1 × ( − 2 ) + 3 × 0 + 2 × ( − 2 ) ∣ 8 × 8 = 1 4 |cos<\overrightarrow{AB_1},\overrightarrow{A_1C}>|=\cfrac{|-1\times (-2)+\sqrt{3}\times 0+2\times(-2)|}{\sqrt{8}\times\sqrt{8}}=\cfrac{1}{4} ∣cos<AB1,A1C>∣=8×8∣−1×(−2)+3×0+2×(−2)∣=41。故选 C C C。
【法2】:立体几何法,补体平移法,将正三棱柱补体为一个底面为菱形的直四棱柱,连结
B
1
D
B_1D
B1D,则
B
1
D
/
/
A
1
C
B_1D//A_1C
B1D//A1C,
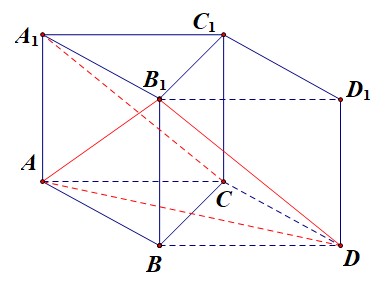
故异面直线
A
B
1
AB_1
AB1与
C
A
1
CA_1
CA1所成角,即转化为共面直线
A
B
1
AB_1
AB1与
B
1
D
B_1D
B1D所成的角
∠
A
B
1
D
\angle AB_1D
∠AB1D,连结
A
D
AD
AD,
在
Δ
A
B
1
D
\Delta AB_1D
ΔAB1D中,
A
B
=
A
A
1
=
2
AB=AA_1=2
AB=AA1=2,可得
A
B
1
=
B
1
D
=
2
2
AB_1=B_1D=2\sqrt{2}
AB1=B1D=22,
A
D
=
2
3
AD=2\sqrt{3}
AD=23,
由余弦定理可知,
c
o
s
∠
A
B
1
D
=
(
2
2
)
2
+
(
2
2
)
2
−
(
2
3
)
2
2
×
2
2
×
2
3
=
1
4
cos\angle AB_1D=\cfrac{(2\sqrt{2})^2+(2\sqrt{2})^2-(2\sqrt{3})^2}{2\times 2\sqrt{2}\times 2\sqrt{3}}=\cfrac{1}{4}
cos∠AB1D=2×22×23(22)2+(22)2−(23)2=41,
故所求为
1
4
\cfrac{1}{4}
41,故选
C
C
C。
- 三棱锥中的建系,建立空间直角坐标系;
【2018年全国卷Ⅰ第18题】如图,四边形 A B C D ABCD ABCD为正方形, E E E, F F F分别为 A D AD AD, B C BC BC的中点,以 D F DF DF为折痕把 △ D F C \triangle DFC △DFC折起,使点 C C C到达点 P P P的位置,且 P F ⊥ B F PF\perp BF PF⊥BF,

(1).证明:平面 P E F ⊥ PEF\perp PEF⊥平面 A B F D ABFD ABFD;
证明:由已知可得, B F ⊥ P F BF\perp PF BF⊥PF, B F ⊥ E F BF\perp EF BF⊥EF,
又 P F ∩ E F = F PF\cap EF=F PF∩EF=F, P F ⊆ PF\subseteq PF⊆平面 P E F PEF PEF, E F ⊆ EF\subseteq EF⊆平面 P E F PEF PEF,
所以 B F ⊥ BF\perp BF⊥平面 P E F PEF PEF,又 B F ⊆ BF\subseteq BF⊆平面 A B F D ABFD ABFD,
所以平面 P E F ⊥ PEF\perp PEF⊥平面 A B F D ABFD ABFD;
(2).求 D P DP DP与平面 A B F D ABFD ABFD所成角的正弦值。
解:作 P H ⊥ E F PH\perp EF PH⊥EF,垂足为 H H H,由(1)得, P H ⊥ PH\perp PH⊥平面 A B F D ABFD ABFD,以 H H H为坐标原点, H F → \overrightarrow{HF} HF的方向为 y y y轴正方向, ∣ B F → ∣ |\overrightarrow{BF}| ∣BF∣为单位长,建立如图所示的空间直角坐标系 H − x y z H-xyz H−xyz,

由(1)得到, D E ⊥ P E DE\perp PE DE⊥PE,又 D P = 2 DP=2 DP=2, D E = 1 DE=1 DE=1,所以 P E = 3 PE=\sqrt{3} PE=3,
又 P F = 1 PF=1 PF=1, E F = 2 EF=2 EF=2,所以 P E ⊥ P F PE\perp PF PE⊥PF,可得 P H = 3 2 PH=\cfrac{\sqrt{3}}{2} PH=23, E H = 3 2 EH=\cfrac{3}{2} EH=23,
则 H ( 0 , 0 , 0 ) H(0,0,0) H(0,0,0), P ( 0 , 0 , 3 2 ) P(0,0,\cfrac{\sqrt{3}}{2}) P(0,0,23), D ( − 1 , − 3 2 , 0 ) D(-1,-\cfrac{3}{2},0) D(−1,−23,0),
则 D P → = ( 1 , 3 2 , 3 2 ) \overrightarrow{DP}=(1,\cfrac{3}{2},\cfrac{\sqrt{3}}{2}) DP=(1,23,23), H P → = ( 0 , 0 , 3 2 ) \overrightarrow{HP}=(0,0,\cfrac{\sqrt{3}}{2}) HP=(0,0,23)为平面 A B F D ABFD ABFD的法向量,
设 D P DP DP与平面 A B F D ABFD ABFD所成角为 θ \theta θ,则 s i n θ = ∣ c o s < H P → , D P → > ∣ = ∣ H P → ⋅ D P → ∣ H P → ∣ ∣ D P → ∣ ∣ = 3 4 3 = 3 4 sin\theta=|cos<\overrightarrow{HP},\overrightarrow{DP}>|=|\cfrac{\overrightarrow{HP}\cdot \overrightarrow{DP}}{|\overrightarrow{HP}||\overrightarrow{DP}|}|=\cfrac{\frac{3}{4}}{\sqrt{3}}=\cfrac{\sqrt{3}}{4} sinθ=∣cos<HP,DP>∣=∣∣HP∣∣DP∣HP⋅DP∣=343=43,
所以 D P DP DP与平面 A B F D ABFD ABFD所成角的正弦值为 3 4 \cfrac{\sqrt{3}}{4} 43。
- 长方体中的建系,建立空间直角坐标系;
【长方体中建系】【2019年高考数学试卷理科新课标Ⅱ第17题】如图,长方体 A B C D − A 1 B 1 C 1 D 1 ABCD-A_1B_1C_1D_1 ABCD−A1B1C1D1的底面 A B C D ABCD ABCD是正方形,点 E E E在棱 A A 1 AA_1 AA1上, B E ⊥ E C 1 BE\perp EC_1 BE⊥EC1.
(1).证明: B E ⊥ BE\perp BE⊥平面 E B 1 C 1 EB_1C_1 EB1C1;
分析:需要证明线面垂直,往往先要转化为证明线线垂直;
解析:由已知 B 1 C 1 ⊥ B_1C_1\perp B1C1⊥平面 A B B 1 A 1 ABB_1A_1 ABB1A1, B E ⊂ BE\subset BE⊂平面 A B B 1 A 1 ABB_1A_1 ABB1A1,故 B 1 C 1 ⊥ B E B_1C_1\perp BE B1C1⊥BE,
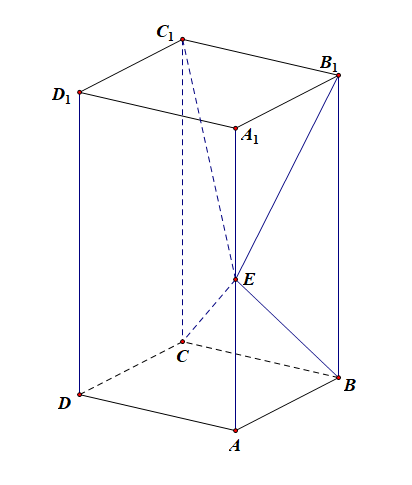
又 B E ⊥ E C 1 BE\perp EC_1 BE⊥EC1, B 1 C 1 ⊂ B_1C_1\subset B1C1⊂平面 E B 1 C 1 EB_1C_1 EB1C1, E C 1 ⊂ EC_1\subset EC1⊂平面 E B 1 C 1 EB_1C_1 EB1C1, B 1 C 1 ∩ E C 1 = C 1 B_1C_1\cap EC_1=C_1 B1C1∩EC1=C1,
故 B E ⊥ BE\perp BE⊥平面 E B 1 C 1 EB_1C_1 EB1C1;
(2).若 A E = A 1 E AE=A_1E AE=A1E,求二面角 B − E C − C 1 B-EC-C_1 B−EC−C1的正弦值;
解析:由(1)知道 ∠ B E B 1 = 9 0 ∘ \angle BEB_1=90^{\circ} ∠BEB1=90∘,由题设可知 R t △ A B E R t △ A 1 B 1 E Rt\triangle ABE Rt\triangle A_1B_1E Rt△ABERt△A1B1E,所以 ∠ A E B = 4 5 ∘ \angle AEB=45^{\circ} ∠AEB=45∘,故 A E = A B AE=AB AE=AB, A A 1 = 2 A B AA_1=2AB AA1=2AB,
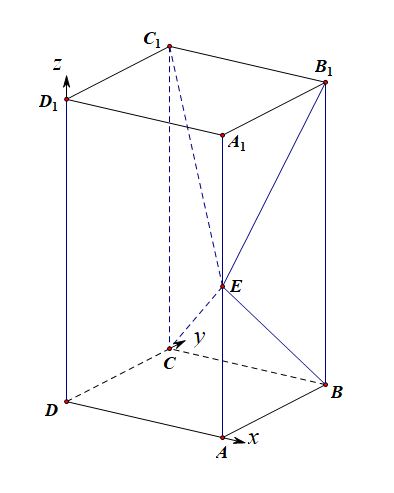
以 D D D为坐标原点, D A → \overrightarrow{DA} DA的方向为 x x x轴的正方向, ∣ D A → ∣ |\overrightarrow{DA}| ∣DA∣为单位长,建立如图所示的空间直角坐标系 D − x y z D-xyz D−xyz,
则 C ( 0 , 1 , 0 ) C(0,1,0) C(0,1,0), B ( 1 , 1 , 0 ) B(1,1,0) B(1,1,0), C 1 ( 0 , 1 , 2 ) C_1(0,1,2) C1(0,1,2), E ( 1 , 0 , 1 ) E(1,0,1) E(1,0,1), C B → = ( 1 , 0 , 0 ) \overrightarrow{CB}=(1,0,0) CB=(1,0,0), C E → = ( 1 , − 1 , 1 ) \overrightarrow{CE}=(1,-1,1) CE=(1,−1,1), C C 1 → = ( 0 , 0 , 2 ) \overrightarrow{CC_1}=(0,0,2) CC1=(0,0,2),
设平面 E B C EBC EBC的法向量 n ⃗ = ( x , y , z ) \vec{n}=(x,y,z) n=(x,y,z),
则 { C B → ⋅ n ⃗ = 0 C E → ⋅ n ⃗ = 0 \left\{\begin{array}{l}{\overrightarrow{CB}\cdot \vec{n}=0}\\{\overrightarrow{CE}\cdot \vec{n}=0}\end{array}\right. {CB⋅n=0CE⋅n=0,即 { x = 0 x − y + z = 0 \left\{\begin{array}{l}{x=0}\\{x-y+z=0}\end{array}\right. {x=0x−y+z=0,所以可以赋值取 n ⃗ = ( 0 , − 1 , − 1 ) \vec{n}=(0,-1,-1) n=(0,−1,−1),
设平面 E C C 1 ECC_1 ECC1的法向量 m ⃗ = ( x , y , z ) \vec{m}=(x,y,z) m=(x,y,z),
则 { C C 1 → ⋅ m ⃗ = 0 C E → ⋅ m ⃗ = 0 \left\{\begin{array}{l}{\overrightarrow{CC_1}\cdot \vec{m}=0}\\{\overrightarrow{CE}\cdot \vec{m}=0}\end{array}\right. {CC1⋅m=0CE⋅m=0,即 { 2 z = 0 x − y + z = 0 \left\{\begin{array}{l}{2z=0}\\{x-y+z=0}\end{array}\right. {2z=0x−y+z=0,所以可以赋值取 m ⃗ = ( 1 , 1 , 0 ) \vec{m}=(1,1,0) m=(1,1,0),
于是, c o s < n ⃗ , m ⃗ > = n ⃗ ⋅ m ⃗ ∣ n ⃗ ∣ ∣ m ⃗ ∣ = − 1 2 cos<\vec{n},\vec{m}>=\cfrac{\vec{n}\cdot\vec{m}}{|\vec{n}||\vec{m}|}=-\cfrac{1}{2} cos<n,m>=∣n∣∣m∣n⋅m=−21,
即 < n ⃗ , m ⃗ > = 12 0 ∘ <\vec{n},\vec{m}>=120^{\circ} <n,m>=120∘,所以,二面角 B − E C − C 1 B-EC-C_1 B−EC−C1的正弦值为 3 2 \cfrac{\sqrt{3}}{2} 23。
解后反思:当然,本题目同样可用点 C C C做为坐标原点来建立坐标系。
- 建系不难,难点在点的坐标确定,新考向;
【四棱锥中建系】如图,在四棱锥 P − A B C D P-ABCD P−ABCD中, P D ⊥ PD\perp PD⊥平面 A B C D ABCD ABCD,四边形 A B C D ABCD ABCD是菱形,且 A C AC AC, B D BD BD交于点 O O O, E E E是 P B PB PB上任意一点。

(1)求证:平面 E A C ⊥ EAC\perp EAC⊥ 平面 B P D BPD BPD;
分析:由于 P D ⊥ PD\perp PD⊥平面 A B C D ABCD ABCD,所以 P D ⊥ A C PD\perp AC PD⊥AC,
由于四边形 A B C D ABCD ABCD是菱形,所以 B D ⊥ A C BD\perp AC BD⊥AC,
又由于 B D ∩ P D = D BD\cap PD=D BD∩PD=D,所以 A C ⊥ AC\perp AC⊥ 平面 P B D PBD PBD,
又由于 A C ⊆ AC\subseteq AC⊆ 平面 A E C AEC AEC,所以平面 E A C ⊥ EAC\perp EAC⊥ 平面 B P D BPD BPD;
(2)若 E E E为 P B PB PB的中点, A C = 2 AC=2 AC=2, B D = 2 3 BD=2\sqrt{3} BD=23,且二面角 A − P B − D A-PB-D A−PB−D的余弦值为 21 7 \cfrac{\sqrt{21}}{7} 721,求四棱锥 P − A B C D P-ABCD P−ABCD的体积;

分析:连接 O E OE OE,在 △ P B D \triangle PBD △PBD中, E O / / P D EO//PD EO//PD,所以 E O ⊥ EO\perp EO⊥平面 A B C D ABCD ABCD,分别以 O A OA OA, O B OB OB, O E OE OE所在直线为 x x x轴, y y y轴, z z z轴建立如图所示的空间直角坐标系,设 P D = t PD=t PD=t,则 A ( 1 , 0 , 0 ) A(1,0,0) A(1,0,0), B ( 0 , 3 , 0 ) B(0,\sqrt{3},0) B(0,3,0), C ( − 1 , 0 , 0 ) C(-1,0,0) C(−1,0,0), E ( 0 , 0 , t 2 ) E(0,0,\cfrac{t}{2}) E(0,0,2t), P ( 0 , − 3 , t ) P(0,-\sqrt{3},t) P(0,−3,t),
设平面 P A B PAB PAB的一个法向量为 n ⃗ = ( x , y , z ) \vec{n}=(x,y,z) n=(x,y,z),
则 { n ⃗ ⋅ A B → = − x + 3 y = 0 n ⃗ ⋅ A P → = − x − 3 y + t z = 0 \left\{\begin{array}{l}{\vec{n}\cdot \overrightarrow{AB}=-x+\sqrt{3}y=0}\\{\vec{n}\cdot \overrightarrow{AP}=-x-\sqrt{3}y+tz=0}\end{array}\right. {n⋅AB=−x+3y=0n⋅AP=−x−3y+tz=0 令 y = 1 y=1 y=1,得到 n ⃗ = ( 3 , 1 , 2 3 t ) \vec{n}=(\sqrt{3},1,\cfrac{2\sqrt{3}}{t}) n=(3,1,t23),
平面 P B D PBD PBD的法向量 m ⃗ = ( 1 , 0 , 0 ) \vec{m}=(1,0,0) m=(1,0,0),
由于二面角 A − P B − D A-PB-D A−PB−D的余弦值为 21 7 \cfrac{\sqrt{21}}{7} 721,则 ∣ c o s < m ⃗ , n ⃗ > ∣ = 3 4 + 12 t 2 = 21 7 |cos<\vec{m},\vec{n}>|=\cfrac{\sqrt{3}}{\sqrt{4+\frac{12}{t^2}}}=\cfrac{\sqrt{21}}{7} ∣cos<m,n>∣=4+t2123=721
解得 t = 2 t=2 t=2或 t = − 2 t=-2 t=−2(舍去),故四棱锥 P − A B C D P-ABCD P−ABCD的体积为 V = 1 3 × 1 2 × 2 × 2 3 × 2 = 4 3 3 V=\cfrac{1}{3}\times \cfrac{1}{2}\times 2\times 2\sqrt{3}\times 2=\cfrac{4\sqrt{3}}{3} V=31×21×2×23×2=343;

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










