线段树基础（上）

普通线段树

线段树原理

（证明）

线段树是一种维护序列操作的二叉树数据结构。

线段树存在以下五个操作：

1. build：创建一颗线段树
2. push_up：根据子节点计算父节点的信息
3. push_down：根据父节点的修改标记去更新子节点的信息（用于区间修改）
4. push：修改（分为单点修改和区间修改）
5. find：查询

可以证明，线段树是一颗Leafy tree，也就是说，它的非叶子点一定有左右儿子。

线段树的节点对应着序列上的一段区间。对于一段长度为$n$的区间，根节点对应着$[1,n]$，对于一个对应区间为$[l,r]$的节点，令$mid=\lfloor \frac{l+r}{2}\rfloor$，则它的左儿子对应的区间为$[l,mid]$，右儿子对应的区间为$[mid+1,r]$。

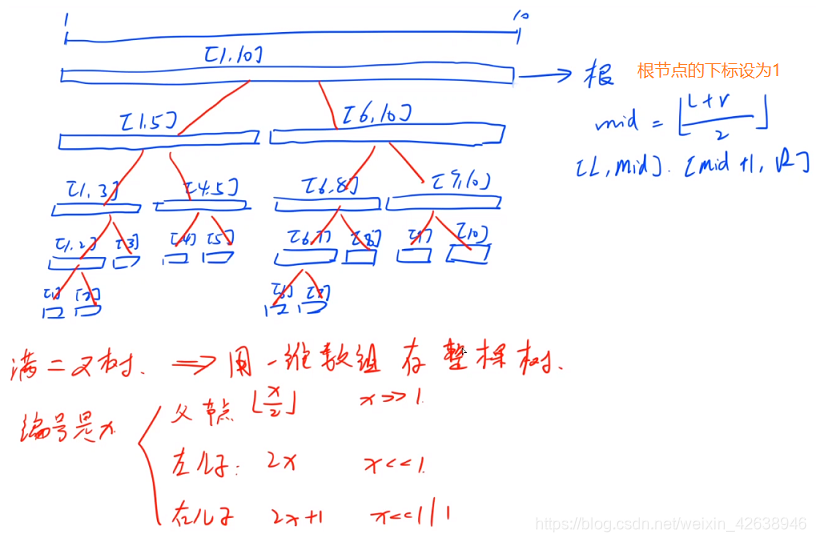
普通线段树一个节点用一个结构体表示：

struct node{
	int l,r;节点对应的区间范围

	int info;节点存储的某些信息
};

通常我们把一颗线段树用堆式存储在数组里。即根节点编号为$1$，编号为$u$的节点左儿子为$2\cdot u$，右儿子为$2\cdot u+1$。相应的，$u$节点的父亲编号为$\lfloor \frac{u}{2}\rfloor$。

对于对应区间为$[1,N]$的一颗线段树，可以证明，它用到的空间可以存储在大小为$4N$的数组以内。
因此我们通常这样定义一颗线段树：

const int N=1e5;
struct node{
	int l,r;
	int info;//...
}t[N<<2];

习惯上线段树对应的区间是从$1$开始编号的，例如$[1,n]$。但其实线段树也可以维护从$0$开始编号的区间。但是如果区间从负数开始编号，则需要对线段树的实现进行特殊处理，或者增加一个偏移量。（这是由于c++默认的int取整方式不是向下取整，而是向零取整）
不过如果习惯把(l+r)/2写成l+r>>1，那就不需要特殊处理，因为右移恰好是向下取整。

需要尤其注意的是，对应的区间为$[0,n]$的一颗线段树，事实上对应的区间长度为$n+1$，因此空间需要开到$4(n+1)$，而不是$4n$。

可以证明，线段树大概有$O({\log }_{2}n)$层。

P3374

线段树维护单点加区间求和。

我们要实现快速进行区间求和，因此线段树节点还要额外维护区间和（sum）。

const int N=5e5;
struct node{
	int l,r;
	int sum; 
}t[N<<2];

建树（build）

然后我们通过build创建一颗线段树。（默认线段树维护一个全$0$序列）
build(u,l,r)递归到节点$u$，设置这个节点的对应的区间为$[l,r]$，然后递归到它的左右儿子。

void build(int u,int l,int r) {
	t[u]={l,r,0};
	if(l==r) return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
}

每个节点只被创建一次，因此build的复杂度是$O(n\log n)$

上传标记（push_up）

push_up(u)表示$u$为父亲，现在用$u$的左右儿子的信息来合并$u$的信息。
我们约定调用push_up(u)的前提是，$u$必须要有左右儿子。

在这个题目里面，我们维护的是区间和。

void push_up(int u) {
	t[u].sum=t[u<<1].sum+t[u<<1|1].sum;
}

单点修改（push）

想要在线段树上做单点修改，我们需要根节点一直递归下去到对应为止的节点，并更新递归路径上所有节点的信息。

push(u,pos,val)，表示目前在编号为$u$的节点，修改操作为，给$pos$位置的值增加$val$。
我们从根节点出发开始递归，我们递归进入编号为$u$的节点，前提是$pos\in [l_u,r_u]$。

单点修改的push函数具体是这样运作的：

• 若$u$为叶子，因为$pos\in [l_u,r_u]$才会递归下来，说明$pos=l_u=r_u$，进行修改
• 若$u$不是叶子，要递归到$pos$对应方向的儿子，然后push_up(u)，更新$u$节点的信息
  这里能够push_up(u)，是因为$u$有儿子，说明$u$不是叶子。

void push(int u,int p,int val) {
	if(t[u].l==t[u].r&&t[u].r==p) t[u].sum+=val;
	else {
		int mid=t[u].l+t[u].r>>1;
		if(p<=mid) push(u<<1,p,val);
		if(mid<p) push(u<<1|1,p,val);
		第二个if(mid<p)可以改为else，但是由于区间修改不能这么写，习惯上不这么写。
		
		push_up(u);
	}
}

这样我们的递归路线最终形成了线段树上一条从根节点到叶子节点的路径：

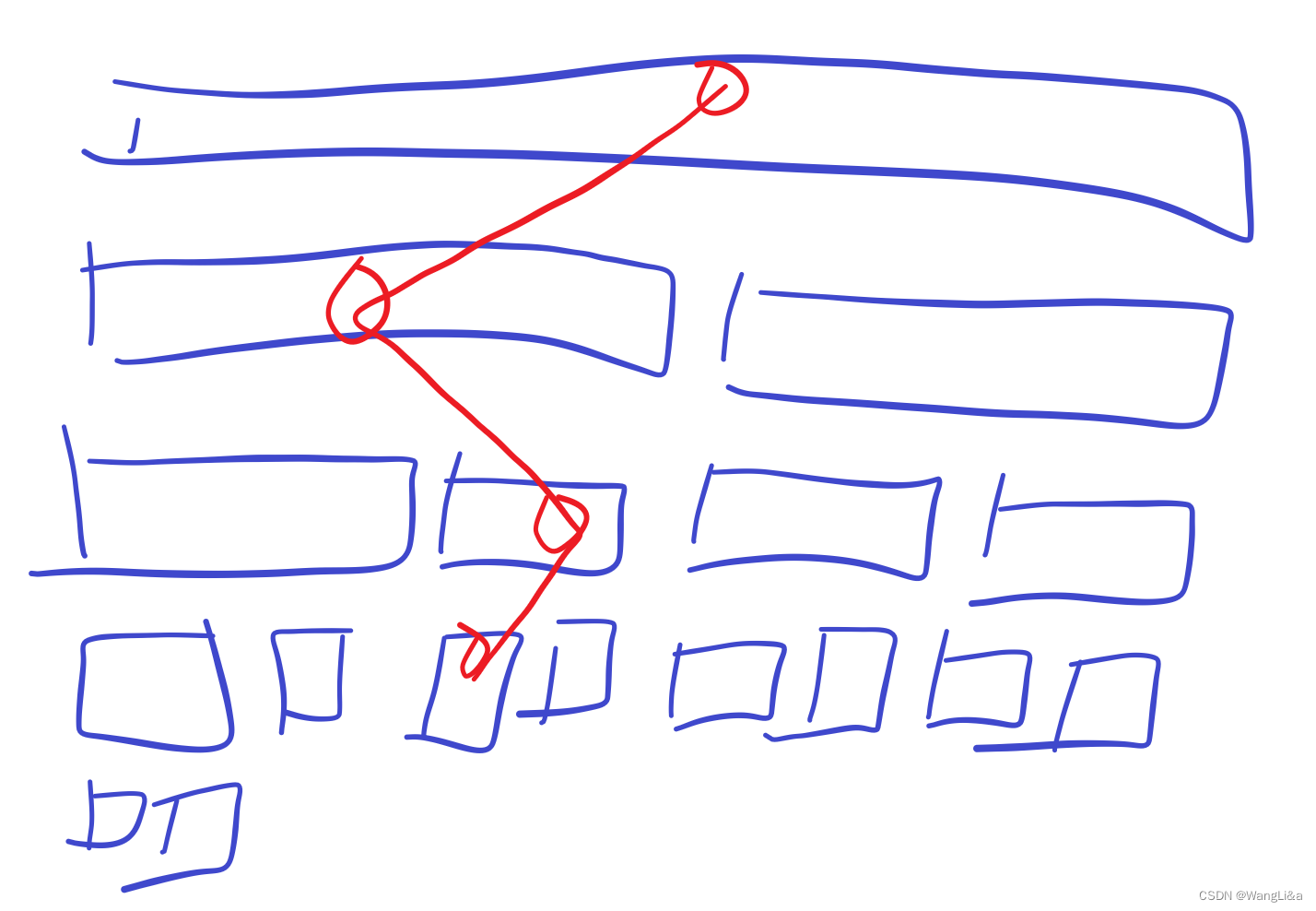
单点修改的复杂度与树高有关，因此复杂度为$O(\log n)$

查询（find）

查询操作find(u,l,r)表示目前递归到了节点$u$，要查询区间$[l,r]$的和。
能够递归到节点$u$，前提是$u$与$[l,r]$有交。

find函数具体是这样运作的：

• 如果节点$u$包含于$[l,r]$，则返回$su{m}_u$
• 否则：令$mid=\lfloor \frac{l+r}{2}\rfloor$
• 若$l\le mid$，说明区间与左儿子有交，递归到左儿子
  之所以$l\le mid$就说明区间与左儿子有交，是因为保证了$[l,r]$与$u$有交，右儿子同理。
• 若$mid<r$，说明区间与右儿子有交，递归到右儿子

int find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;包含就返回
	int mid=t[u].l+t[u].r>>1;不包含就递归到左右儿子
	int ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	注意这里不是else，即使访问了左儿子，右儿子可能需要递归
	
	return ans;
}

这样我们发现，一次区间查询事实上访问了线段树上$O(\log n)$个节点，例如我们要查询区间$[2,8]$，具体来说是这样的：

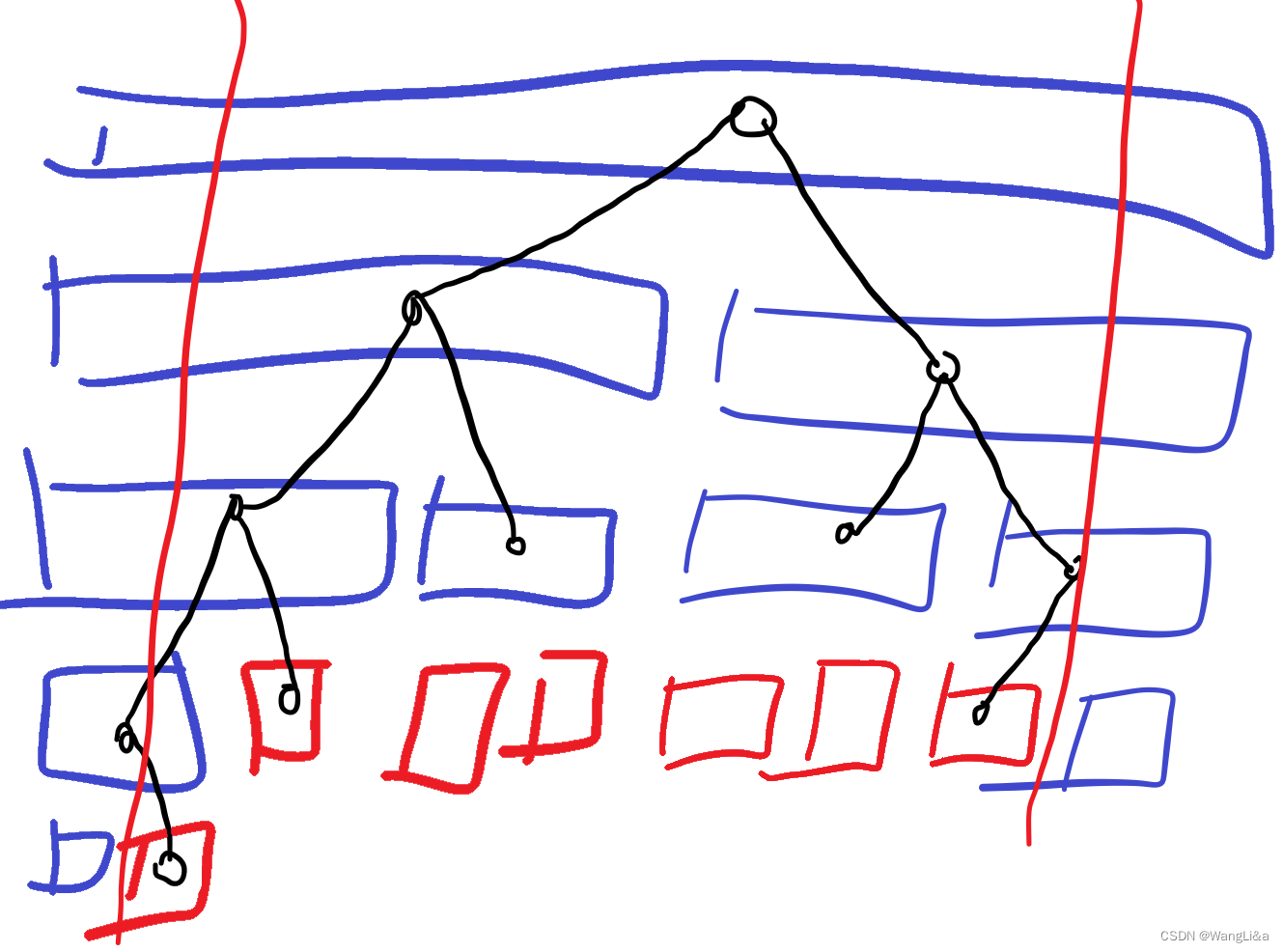
其中黑色节点表示访问到的节点，红色的叶子节点表示实际要查询的区间。

现在我们来分析一下查询操作的时间复杂度。
对于所有与$[l,r]$有交的节点，显然它们一定是连通的，因为与$[l,r]$有交的一个节点的父亲也与$[l,r]$有交，而它们最终都会与根节点连通。

所以他们会形成一个线段树的一个导出连通图，这个图是一颗树。
显然所有可能被访问的节点都位与这棵树上，接下来我们具体分析一下哪些节点会被访问：

• 第一类节点：对于不被$[l,r]$完全包含的节点来说，这样的节点每层最多有$2$个，一个与$l$相交，另一个与$r$相交。因此这样的节点至多有约$O(2\log n)$个。我们认为它们全部被访问（事实也是如此）
  因为如果同一层有多余两个的节点与$l$或$r$相交，则必然有两个节点相交，但同一层节点显然无交。因此一层之中这样的节点最多两个。
• 第二类节点：对于被$[l,r]$完全包含的节点来说，$u$被访问到的充要条件是，$u$的父亲不被$[l,r]$完全包含。也就是说它必须是第一类节点的儿子，显然得到它的数量上界为$O(4\log n)$。
  但是注意到一个第一类节点至多有一个第二类儿子，否则它自身就是第二类节点，显然所以第二类被访问节点的数量至多有$O(2\log n)$个。

线段树的重要思想就是，把一次区间操作对应为线段树上$O(\log n)$个节点。

因此每次查询大约访问$O(4\log n)$个线段树节点，时间复杂度为$O(\log n)$。

实现

剩余的就是主函数部分，没什么好说的。

#include<iostream>
using namespace std;
const int N=5e5;
struct node{
	int l,r;
	int sum; 
}t[N<<2];
void build(int u,int l,int r) {
	t[u]={l,r,0};
	if(l==r) return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
}
void push_up(int u) {
	t[u].sum=t[u<<1].sum+t[u<<1|1].sum;
}
void push(int u,int p,int val) {
	if(t[u].l==t[u].r&&t[u].r==p) t[u].sum+=val;
	else {
		int mid=t[u].l+t[u].r>>1;
		if(p<=mid) push(u<<1,p,val);
		if(mid<p) push(u<<1|1,p,val);
		push_up(u);
	}
}
int find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	int mid=t[u].l+t[u].r>>1;
	int ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	return ans;
}
int main() {
	int n,m;
	cin>>n>>m;
	build(1,1,n);
	for(int i=1,x;i<=n;i++) cin>>x,push(1,i,x);
	while(m--) {
		int op,x,y;
		cin>>op>>x>>y;
		if(op==1) push(1,x,y);
		if(op==2) cout<<find(1,x,y)<<endl;
	}
}

例题2

本题是线段树维护区间修改的模板题。
题目要求维护区间加，区间求和。

我们需要使用push_down操作完成区间修改操作，也称为懒标记（延迟标记）。

具体我们需要在每个线段树节点上维护一个加法懒标记（add）：

struct node{
	int l,r;
	long long sum,add; 
}t[N<<2];

add标记表示$u$的儿子需要完成区间加$add$的操作
（$u$已经完成这个操作，也就是说$su{m}_u$已经计算了$add$操作的影响。）
如果$u$没有儿子，那add标记没有意义。

下放标记（push_down）

具体来说，push_down(u)将$u$的懒标记下放给$u$的两个儿子。所以调用这个函数表示$u$有左右儿子。

void push_down(int u) {
	int l=u<<1,r=u<<1|1;
	下放懒标记：
	t[l].add+=t[u].add;
	t[r].add+=t[u].add;
	处理懒标记对区间和标记的影响：
	t[l].sum+=t[u].add*(t[l].r-t[l].l+1);
	t[r].sum+=t[u].add*(t[r].r-t[r].l+1);
	清空u的懒标记：
	t[u].add=0;
}

在push，find访问到$u$时，如果要访问$u$的儿子，就必须先下放懒标记。

void push(int u,int l,int r,long long val) {
	if(l<=t[u].l&&t[u].r<=r) t[u].sum+=val*(t[u].r-t[u].l+1),t[u].add+=val;
	else {
		push_down(u);下放懒标记
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) push(u<<1,l,r,val);
		if(mid<r) push(u<<1|1,l,r,val);
		push_up(u);上传标记
	}
}
long long find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	push_down(u);下放懒标记
	int mid=t[u].l+t[u].r>>1;
	long long ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	find函数可以不需要push_up，因为push的时候push_up的作用是计算当前push操作对儿子的作用。
	这个作用没有在父亲处计算。（有时也无法在父亲处计算）
	
	而find函数对子节点唯一的影响是，可能会下放懒标记，但push_down的影响在之前计算过了。
	return ans;
}

实现

#include<iostream>
using namespace std;
const int N=1e5;
struct node{
	int l,r;
	long long sum,add; 
}t[N<<2];
void build(int u,int l,int r) {
	t[u]={l,r,0,0};
	if(l==r) return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
}
void push_up(int u) {
	t[u].sum=t[u<<1].sum+t[u<<1|1].sum;
}
void push_down(int u) {
	int l=u<<1,r=u<<1|1;
	t[l].add+=t[u].add;
	t[r].add+=t[u].add;
	t[l].sum+=t[u].add*(t[l].r-t[l].l+1);
	t[r].sum+=t[u].add*(t[r].r-t[r].l+1);
	t[u].add=0;
}
void push(int u,int l,int r,long long val) {
	if(l<=t[u].l&&t[u].r<=r) t[u].sum+=val*(t[u].r-t[u].l+1),t[u].add+=val;
	else {
		push_down(u);
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) push(u<<1,l,r,val);
		if(mid<r) push(u<<1|1,l,r,val);
		push_up(u);
	}
}
long long find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	push_down(u);
	int mid=t[u].l+t[u].r>>1;
	long long ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	return ans;
}
int main() {
	int n,m;
	cin>>n>>m;
	build(1,1,n);
	for(long long i=1,x;i<=n;i++) cin>>x,push(1,i,i,x);
	while(m--) {
		int op,x,y;
		cin>>op>>x>>y;
		if(op==1) {
			long long k;
			cin>>k;
			push(1,x,y,k);
		}
		if(op==2) cout<<find(1,x,y)<<endl;
	}
}

例题3

本题要求同时维护区间加乘，区间求和。因此需要维护比较复杂的懒标记。

我们需要维护三个标记，分别是区间和标记（sum）、区间加标记（add）、区间乘标记（mul）

如何维护加乘标记的合并呢？假设我们把对一个节点的操作写出来，它可能是则这样的：
$+x,+y,\times z,\times w,+p,\times q$

假设这个节点的区间和为$sum$，则它依次变为：
$sum+x$
$sum+x+y$
$(sum+x+y)\times z$
$(sum+x+y)\times z\times w$
$(sum+x+y)\times z\times w+p$
$((sum+x+y)\times z\times w+p)\times q$

首先我们知道可以把同类操作合并起来。那操作序列就变成了一个加乘交错序列。

如何把加乘交错的变化维护在一个节点上呢。
有一种观察是：
$sum\times mul+add=sum\times mul+add$
$(sum+add)\times mul=sum\times mum+add\times mul$

这说明先乘后加的话，对乘法标记没有影响。先加后乘，则加法标记可以分配出来。

因此我们维护一个$k\cdot x+b$的形式，表示懒标记将对它的儿子先乘后加的做修改。

这时候懒标记的作用是有先后顺序的。

（这时候就会有人会问了，能不能维护先加后乘呢？）
其实是不行的，如果维护$k(x+b)$的懒标记修改形式的话，那对于先乘后加的修改序列维护起来是方便了，但是如果要维护先乘后加的话，会发生什么呢？
$x\to k\cdot x\to k\cdot x+b=k\left(x+\frac{b}{k}\right)$，出现了分数，这是不好的。

我们具体这样维护标记：

struct node{
	int l,r;
	long long sum,add,mul; 
}t[N<<2];

乘法修改（set_mul）

如果要对节点进行一次乘法，懒标记的改动用set_mul函数实现：
$(mu{l}_u\times su{m}_u+ad{d}_u)\times mul=(mu{l}_u\times mul)\times sum+(ad{d}_u\times mul)$

$mu{l}_u\leftarrow mu{l}_u\times mul$
$ad{d}_u\leftarrow ad{d}_u\times mul$

void set_mul(int u,long long mul) {
	(t[u].add*=mul)%=M;
	(t[u].mul*=mul)%=M; 
	(t[u].sum*=mul)%=M;
}

加法修改（set_add）

如果要对节点进行一次加法，懒标记的改动用set_add函数实现：

void set_add(int u,long long add) {
	(t[u].add+=add)%=M;
	(t[u].sum+=add*(t[u].r-t[u].l+1))%=M;注意加法操作对于sum的影响要乘以区间长度
}

下放标记（push_down）

标记下放相当于对子节点进行修改，注意先乘后加。

void push_down(int u) {
	set_mul(u<<1,t[u].mul);
	set_mul(u<<1|1,t[u].mul);
	set_add(u<<1,t[u].add);
	set_add(u<<1|1,t[u].add);
	t[u].mul=1;
	t[u].add=0;
}

这样的话，修改也有两个版本，一个是区间加，一个是区间乘法：

void pushadd(int u,int l,int r,long long add) {
	if(l<=t[u].l&&t[u].r<=r) set_add(u,add);
	else {
		push_down(u);
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) pushadd(u<<1,l,r,add);
		if(mid<r) pushadd(u<<1|1,l,r,add);
		push_up(u);
	}
}
void pushmul(int u,int l,int r,long long mul) {
	if(l<=t[u].l&&t[u].r<=r) set_mul(u,mul);
	else {
		push_down(u);
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) pushmul(u<<1,l,r,mul);
		if(mid<r) pushmul(u<<1|1,l,r,mul);
		push_up(u);
	}
}

实现

#include<iostream>
using namespace std;
const int N=1e5;
long long M; 
struct node{
	int l,r;
	long long sum,add,mul; 
}t[N<<2];
void build(int u,int l,int r) {
	t[u]={l,r,0,0,1};
	if(l==r) return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
}
void push_up(int u) {
	(t[u].sum=t[u<<1].sum+t[u<<1|1].sum)%=M;
}
void set_mul(int u,long long mul) {
	(t[u].add*=mul)%=M;
	(t[u].mul*=mul)%=M; 
	(t[u].sum*=mul)%=M;
}
void set_add(int u,long long add) {
	(t[u].add+=add)%=M;
	(t[u].sum+=add*(t[u].r-t[u].l+1))%=M;
}
void push_down(int u) {
	set_mul(u<<1,t[u].mul);
	set_mul(u<<1|1,t[u].mul);
	set_add(u<<1,t[u].add);
	set_add(u<<1|1,t[u].add);
	t[u].mul=1;
	t[u].add=0;
}
void pushadd(int u,int l,int r,long long add) {
	if(l<=t[u].l&&t[u].r<=r) set_add(u,add);
	else {
		push_down(u);
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) pushadd(u<<1,l,r,add);
		if(mid<r) pushadd(u<<1|1,l,r,add);
		push_up(u);
	}
}
void pushmul(int u,int l,int r,long long mul) {
	if(l<=t[u].l&&t[u].r<=r) set_mul(u,mul);
	else {
		push_down(u);
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) pushmul(u<<1,l,r,mul);
		if(mid<r) pushmul(u<<1|1,l,r,mul);
		push_up(u);
	}
}
long long find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	push_down(u);
	int mid=t[u].l+t[u].r>>1;
	long long ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	return ans%M;
}
int main() {
	int n,m;
	cin>>n>>m>>M;
	build(1,1,n);
	for(long long i=1,x;i<=n;i++) cin>>x,pushadd(1,i,i,x);
	while(m--) {
		int op,l,r;
		long long k;
		cin>>op>>l>>r;
		if(op==1) {
			cin>>k;
			pushmul(1,l,r,k%M);
		}
		if(op==2) {
			cin>>k;
			pushadd(1,l,r,k%M);
		}
		if(op==3) cout<<find(1,l,r)<<endl;
	} 
}

其他题目

P1198
P4588
P1471

权值线段树

通常的线段树是区间树，每个节点对应一段区间。

权值树维护的是值域。
权值线段树即值域线段树，每个节点对应一段值域连续段的信息。
可以认为，权值线段树是维护桶数组的区间线段树。

维护负数值域需要加上偏移，除此之外，写法上来说没有区别。

动态开点线段树

通常的线段树是堆式存储的，这样需要开辟$4N$的空间。事实上宽度为$N$的线段树至多有$2N-1$个节点，只需要开辟$2N$的空间。

更进一步来说，假设对于宽度为$T$的线段树进行$m$次修改操作，那么最多访问到其中的$O(m\log T)$个节点，因此空间只需要开到$O(m\log T)$即可。在$T$很大的时候（例如权值线段树）往往很有帮助。

动态开点权值线段树在空间计算上要尤其注意，防止空间超限。并且要注意$n,m,T$很可能不相等，即使在${\log }_2$中计算，也尽量不要混用。
还要注意，单点修改和区间修改会创建的节点数是不同的，对于宽度为$T$而言，单点修改会创建$\lceil {\log }_{2}T\rceil$个节点，而区间修改会创建$4\lceil {\log }_{2}T\rceil$个节点。

例题1

如果我们枚举顺序$i$，则以$i$为结尾的逆序对数量为，$i$之前的数中比$a_i$大的数的数量。

那么我们考虑这样一个算法：

• 维护一个桶$b$
• 顺序枚举$i$
• 以$i$为结尾的逆序对数量为：桶中比$a_i$大的数的数量$=\sum _{j>a_i}{b}_j$
• 把$a_i$加入桶：$b_{a_i}++$

问题在于桶非常大，不能直接开下。所以可以使用动态开点权值线段树。

首先我们来计算一下空间。这个题值域为$10^9$，由于我们只有单点修改操作，因此一次操作是从根节点到叶子的一条链，至多会创建$\lceil {\log }_{2}T\rceil =30$个节点，共有$N=m=5\times 10^5$次修改操作，所以需要的空间为$30N$

我们这样定义节点：

const int N=5e5;
struct node{
	int l,r,lc,rc;
	int sum; 
}t[N*30];

其中lc表示左儿子编号，rc表示右儿子编号。因为没有再使用堆式存储，而是动态开点了。如果等于$0$就表示没有。

除此以外，我们为了方便再定义两个函数lc(u)，rc(u)，用于获得$u$的左右儿子，如果不存在，就创建一个，因此这两个函数不能用于判断左右儿子是否存在。

int tot;
int&lc(int u) {
	if(t[u].lc) return t[u].lc;
	t[++tot]={t[u].l,t[u].l+t[u].r>>1};
	return t[u].lc=tot;
}
int&rc(int u) {
	if(t[u].rc) return t[u].rc;
	t[++tot]={(t[u].l+t[u].r>>1)+1,t[u].r};
	return t[u].rc=tot;
}

动态开点线段树一般是不需要build函数的，其建树代码只需要创建根节点即可：

t[++tot]={1,int(1e9)};

根节点编号为$1$。

其push_up，push和find函数也有对应的改变，具体看实现。

#include<iostream>
using namespace std;
const int N=5e5;
struct node{
	int l,r,lc,rc;
	int sum; 
}t[N*30];
这个空间事实上是超限的，但是由于洛谷特性只会计算动态内容，加上数据过水就跑过去了。
int tot;
int&lc(int u) {
	if(t[u].lc) return t[u].lc;
	t[++tot]={t[u].l,t[u].l+t[u].r>>1};
	return t[u].lc=tot;
}
int&rc(int u) {
	if(t[u].rc) return t[u].rc;
	t[++tot]={(t[u].l+t[u].r>>1)+1,t[u].r};
	return t[u].rc=tot;
}
void push_up(int u) {
	t[u].sum=t[t[u].lc].sum+t[t[u].rc].sum;
	注意这里如果没有左右儿子我们不希望创建，因此不能使用lc(u),rc(u)函数
	0节点的sum为0
}
void push(int u,int l,int r,int val) {
	if(l<=t[u].l&&t[u].r<=r) t[u].sum++;
	else {
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) push(lc(u),l,r,val);如果没有儿子，push需要创建儿子
		if(mid<r) push(rc(u),l,r,val);
		push_up(u);
	}
}
int find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	int mid=t[u].l+t[u].r>>1;
	int ans=0;
	if(l<=mid&&t[u].lc) ans+=find(lc(u),l,r);
	这里需要先检查有没有儿子，如果有儿子再递归
	检查有无儿子不能使用lc(u)函数，只能用t[u].lc
	if(mid<r&&t[u].rc) ans+=find(rc(u),l,r);
	return ans;
}
int a[N+5];
int main() {
// 	cout<<sizeof t/1e6;
	t[++tot]={1,int(1e9)};
	int n;
	cin>>n;
	for(int i=1;i<=n;i++) cin>>a[i];
	long long ans=0;
	for(int i=1;i<=n;i++) {
		if(a[i]!=1e9) 
		注意我们的find函数不接受l>r的参数，因此需要特判a[i]=1e9，或者建树的时候开大
		当然不加这个判断也跑过去了。（数据真水）
			ans+=find(1,a[i]+1,int(1e9));
		push(1,a[i],a[i],1);
	}
	cout<<ans;
}

标记永久化

通常的区间修改标记，通过在访问该节点时下放懒标记更新儿子节点来实现。永久标记没有下放懒标记的操作，它通过在递归查询计算出对儿子节点的影响来实现区间修改的效果。

并不是所有标记都可以永久化。

例题1

区间加法标记（add）可以永久化。永久加法标记add表示节点$u$对应的区间$[l,r]$在这个节点上被增加了$add$

标记永久化后，各个函数的实现略有不同。

建树（build），修改（push）的实现完全相同。

下放标记（push_up）

由于儿子节点的$sum$不再是它们真实值，而是它们去除了被祖先节点永久化后的加法标记造成的影响之后的值，因此在push_up的时候要把本层的加法标记算上。

我们维护sum为考虑子树内全部标记的区间和。

void push_up(int u) {
	t[u].sum=t[u<<1].sum+t[u<<1|1].sum+t[u].add*(t[u].r-t[u].l+1);
}

查询（find）

查询要注意，在查询时计算本层永久标记对答案的影响。

long long find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	int mid=t[u].l+t[u].r>>1;
	long long ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	return ans+t[u].add*(min(t[u].r,r)-max(t[u].l,l)+1);
	这里加上了t[u].add*(u对应的区间与[l,r]相交的大小)，计算了永久标记对答案的影响。
}

实现

值得一提的是，这里使用long long是不严谨的，因为题设并没有保证这种做法不会爆long long。但是它过了。
#include<iostream>
using namespace std;
const int N=1e5;
struct node {
	int l,r;
	long long sum,add;
}t[N<<2];
void build(int u,int l,int r) {
	t[u]={l,r};
	if(l==r) return ;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
}
void push_up(int u) {
	t[u].sum=t[u<<1].sum+t[u<<1|1].sum+t[u].add*(t[u].r-t[u].l+1);
}
void push(int u,int l,int r,long long add) {
	if(l<=t[u].l&&t[u].r<=r) t[u].add+=add,t[u].sum+=add*(t[u].r-t[u].l+1);
	else {
		int mid=t[u].l+t[u].r>>1;
		if(l<=mid) push(u<<1,l,r,add);
		if(mid<r) push(u<<1|1,l,r,add);
		push_up(u);
	}
}
long long find(int u,int l,int r) {
	if(l<=t[u].l&&t[u].r<=r) return t[u].sum;
	int mid=t[u].l+t[u].r>>1;
	long long ans=0;
	if(l<=mid) ans+=find(u<<1,l,r);
	if(mid<r) ans+=find(u<<1|1,l,r);
	return ans+t[u].add*(min(t[u].r,r)-max(t[u].l,l)+1);
}
int main() {
	int n,m;
	cin>>n>>m;
	build(1,1,n);
	for(long long i=1,x;i<=n;i++) cin>>x,push(1,i,i,x);
	while(m--) {
		int op,l,r;
		long long k;
		cin>>op>>l>>r;
		if(op==1) {
			cin>>k;
			push(1,l,r,k);
		}
		if(op==2) cout<<find(1,l,r)<<endl;
	}
}

常见可永久化标记

标记永久化局限非常大，一般只在不得不使用或使用大幅减少码量时使用。

常见有以下标记单独出现时可以永久化：

• 区间加标记
• 区间乘标记
  区间加乘标记不可永久化
• 扫描线段树标记（线段覆盖标记）
• 李超线段树标记
• 可持久化线段树标记必须永久化

后记

下篇