一些常用函数的拉普拉斯变换

最新推荐文章于 2025-03-15 23:24:06 发布
最新推荐文章于 2025-03-15 23:24:06 发布
阅读量6.6w 收藏 188
点赞数 62
分类专栏： 信号与系统
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/wayne6515/article/details/106072098
版权

一. 冲激 δ ( t ) \bm{δ(t)} δ(t)

单位冲激信号的傅里叶变换和拉普拉斯变换均为1

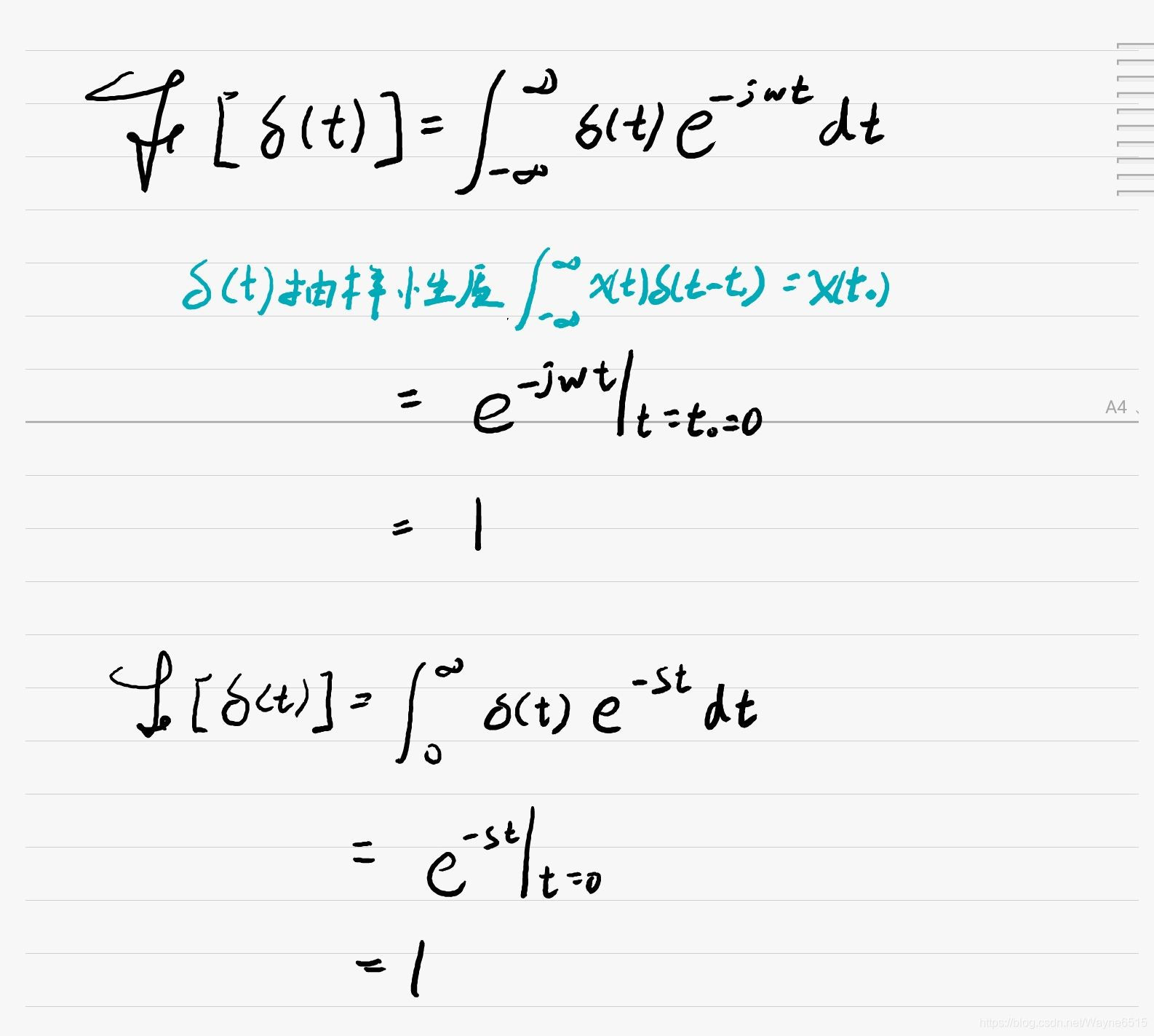
二. 冲激序列

三. 阶跃信号

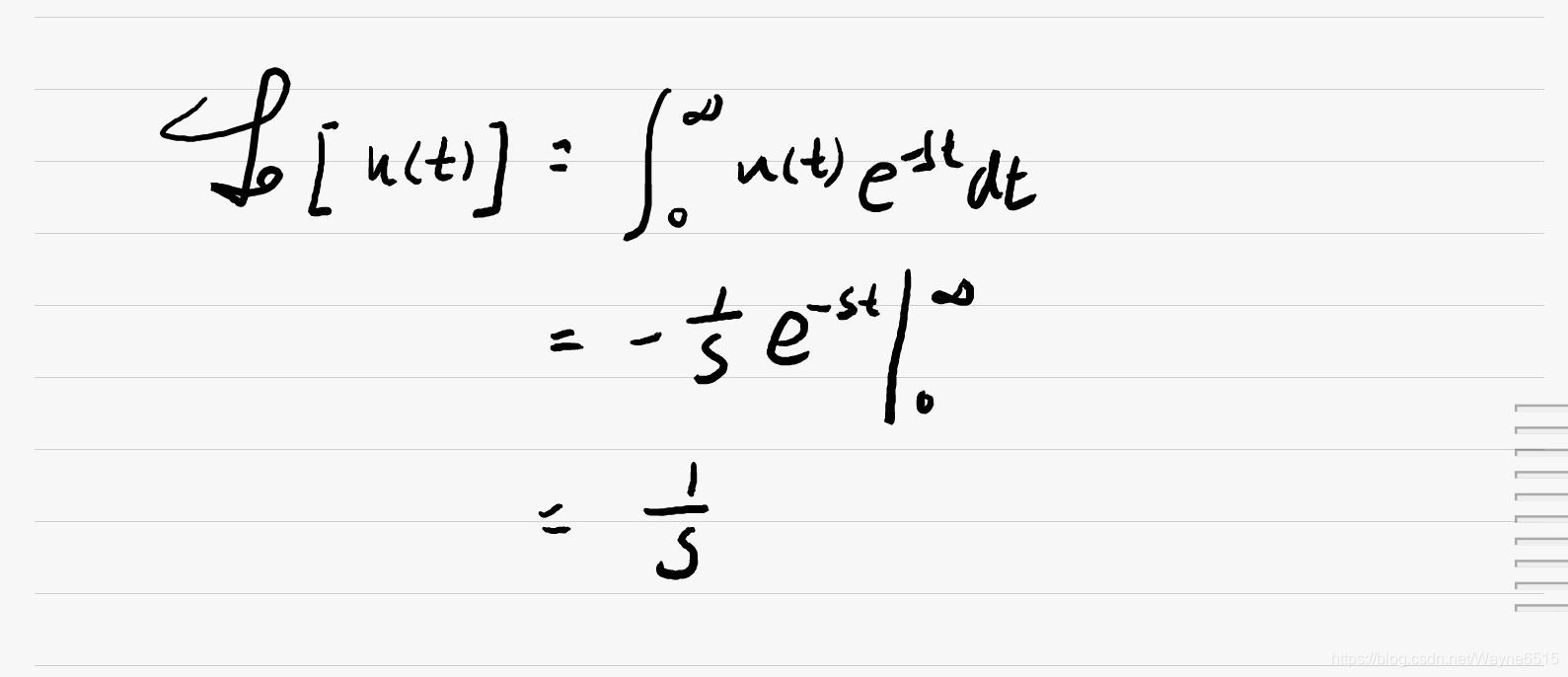
四. 单边指数衰减信号

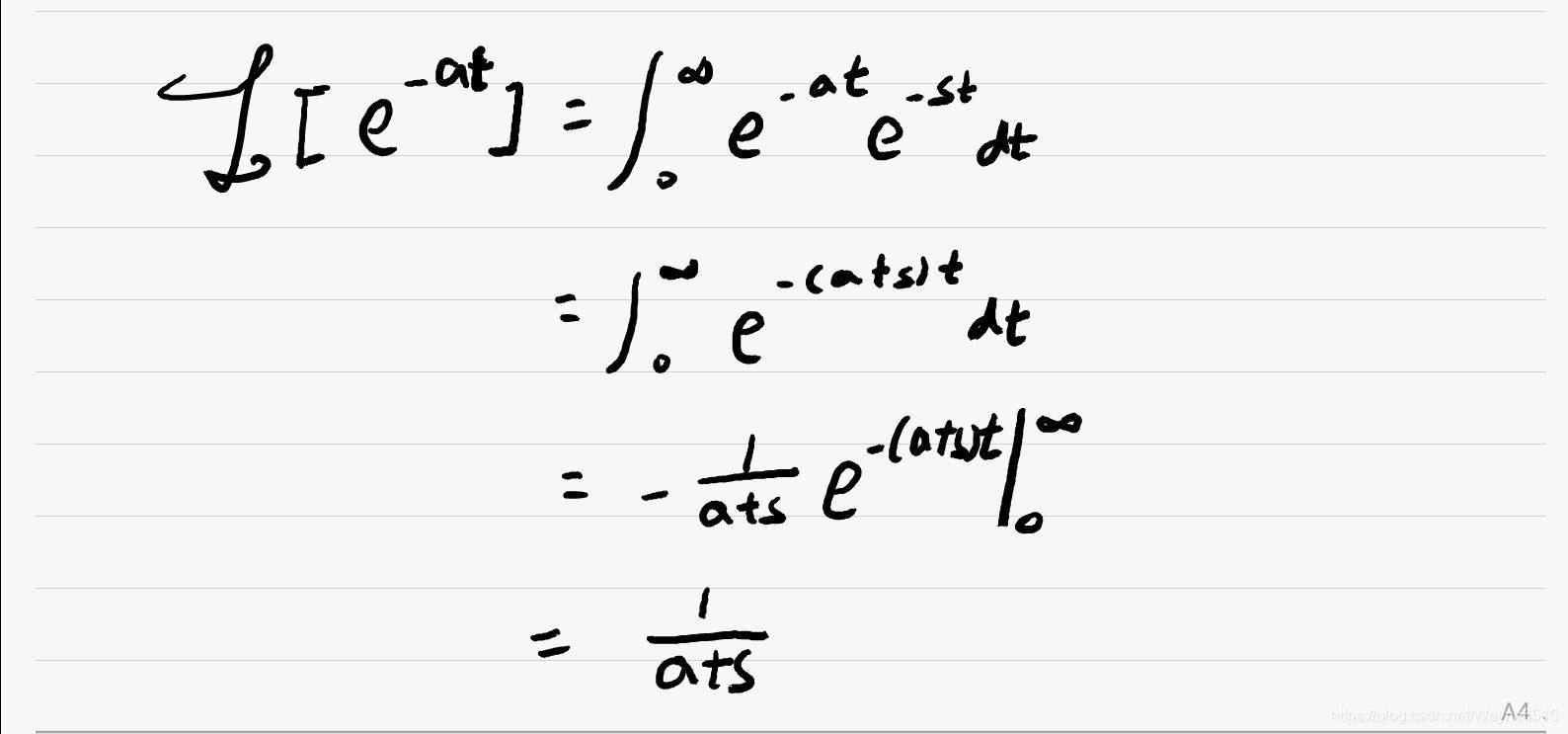
五. t n \bm{t^n} tn

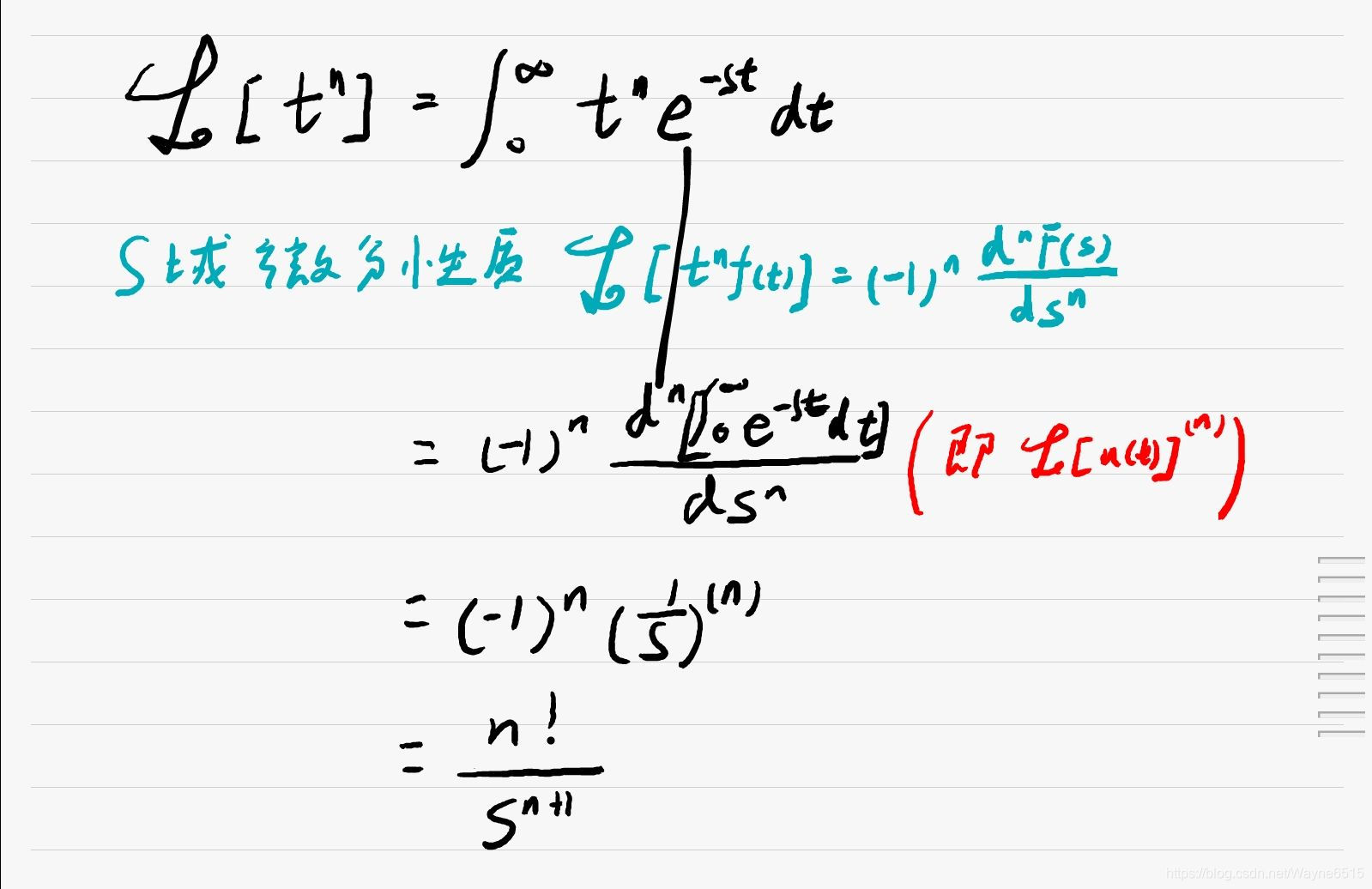
六. s i n ( t ) 和 c o s ( t ) \bm{sin(t)和cos(t)} sin(t)和cos(t)

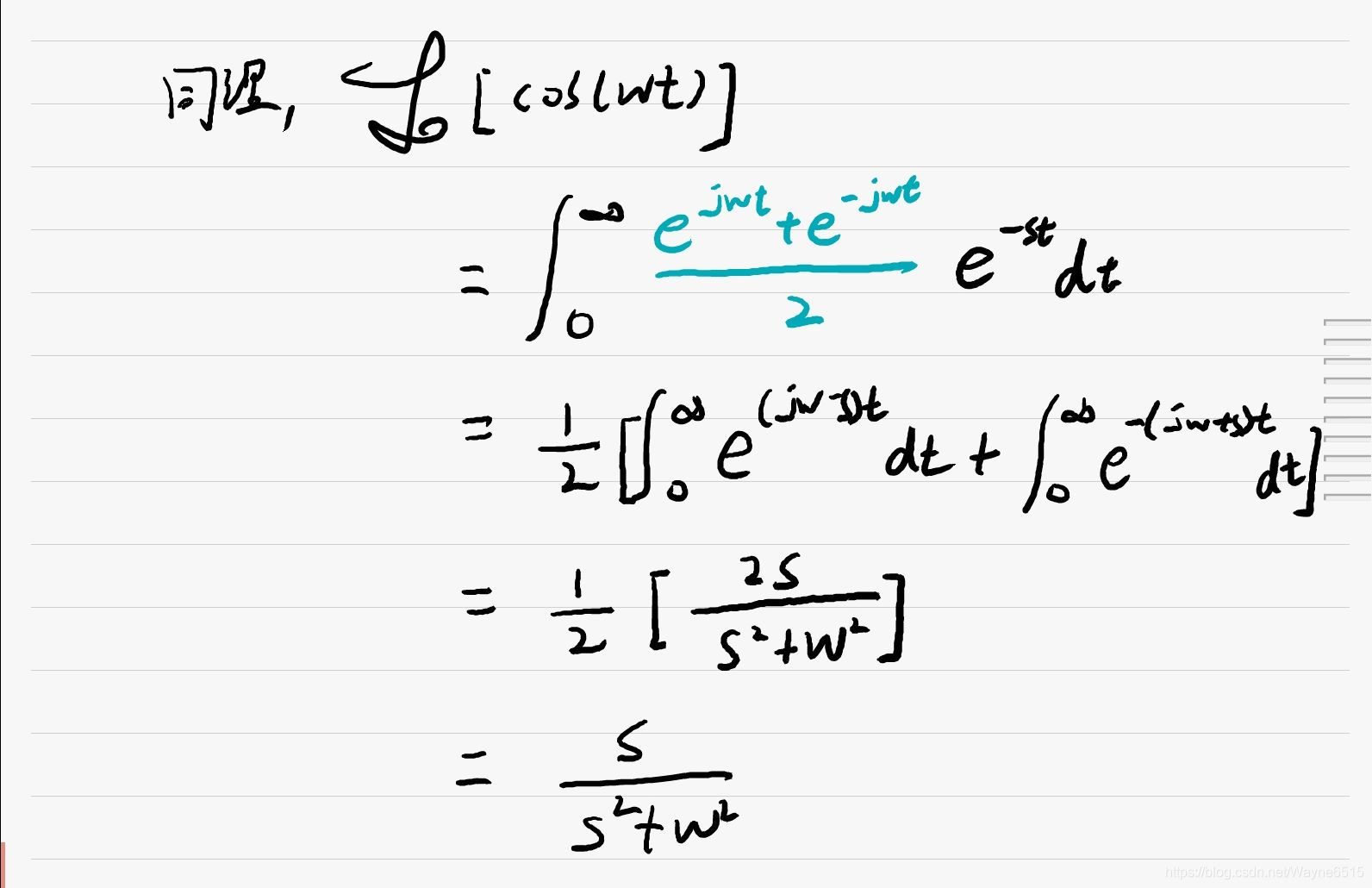
七. e − a t s i n ( w t ) \bm{e^{-at}sin(wt)} e−atsin(wt)和 e − a t c o s ( w t ) \bm{e^{-at}cos(wt)} e−atcos(wt)

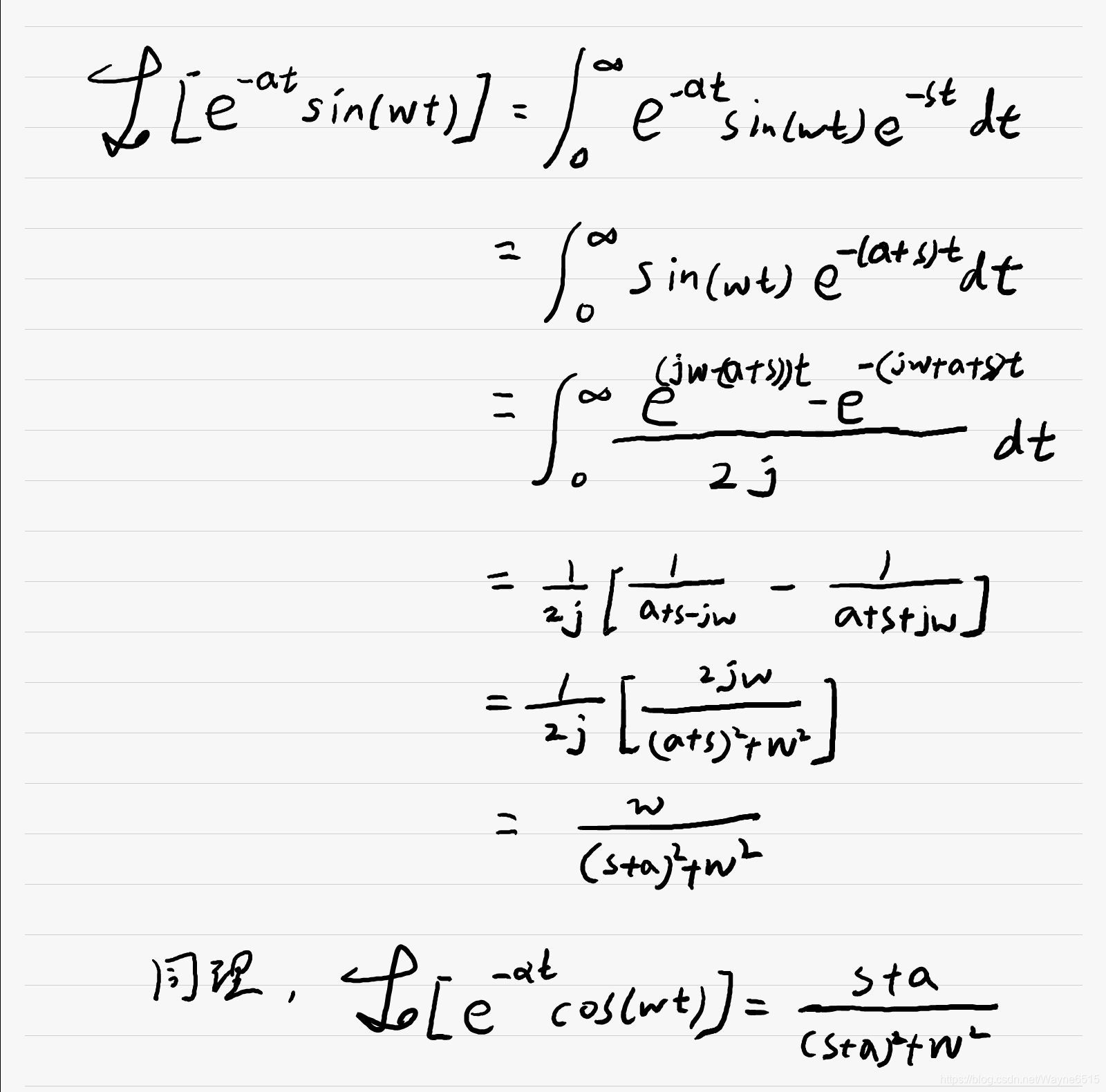
八. t e − a t \bm{te^{-at}} te−at和 t n e − a t \bm{t^{n}e^{-at}} tne−at

九. e − t c o s ( 3 t − 2 ) \bm{e^{-t}cos(3t-2)} e−tcos(3t−2)

拉普拉斯变换
qflook的博客
07-02 748
根据傅里叶变换公式及前提条件得知，傅里叶变换有一些场景并不适用，特别是不能绝对可积的函数来讲（例如f(t)=t，或者f(t)=t*t等），为了扩大应用范围，数学家们想到函数乘以一个逐渐变小的指函数呢，如下：是不是函数就被拉下来可以积分了？如果令，则变成了如下公式：为啥积分范围不是-∞到∞呢，是因为显示中负值没有意义不考虑，这也叫单边拉布拉斯变换。从公式中也可以明显看出，当=0的时候就是傅里叶变换，所以傅里叶变换只是一个特殊的拉普拉斯变换。
常用拉普拉斯变换表（全）
07-20
拉普拉斯变换公式，一共20个公式，对应时域到频域，频域到时域的一般变换。作用很大，喜欢的同学们可以拿走，实用性非常强。
电路中常用的拉普拉斯变换
qq_35912930的博客
04-19 1万+
目录单根共轭复根重根 F(s)=N(s)D(s) F(s) = \frac{N(s)}{D(s)} F(s)=D(s)N(s)​ 步骤一：令D(s)=0D(s) = 0D(s)=0，求其根,p1p_1p1​ 单根 步骤二： F(s)=K1s−p1+K2s−p2+K3s−p3 F(s) = \frac{K_1}{s- p_1} + \frac{K_2}{s- p_2} + \frac{K_3}{s- p_3} F(s)=s−p1​K1​​+s−p2​K2​​+s−p3​K3​​ 步骤三：依次求处KiK_i
拉普拉斯变换推导与常见结论
小黄人的博客
03-15 950
sss令sσjωsσjωsssFsLft∫0−∞fte−stdtFsLft)]∫0−∞​fte−stdtftL−1Fs12πj∫σ−j∞σj∞FsestdsftL−1Fs)]2πj1​∫σ−j∞σj∞​Fsestds。
常用函数的拉氏变换表
狮子雨恋
06-11 1万+
常用函数的拉氏变换表 拉氏变换 KaTeX parse error: Undefined control sequence: \scr at position 2: \̲s̲c̲r̲{L}[f(t)]=F(s)=… 序号 原函数f(t) 象函数F(s) 1 δ(t)\delta (t) δ(t) 1 2 ε(t)\varepsilon (t) ε(t) 1s\frac{1}{s} s1​ 3 t 1s2\frac{1}{s^2}s21​ 4 tn−1(n−1)!,n=1,2,.
拉普拉斯变换公式表_8种常见的拉普拉斯变换，想搞不懂都难
热门推荐
weixin_39928106的博客
12-08 10万+
​拉普拉斯变换(拉氏变换)是一种解线性微分方程的简便运算方法，是分析研究线性动态系统的有力数学工具。简单点说，我们可以使用它去解线性微分方程，而控制工程中的大多数动态系统可由线性微分方程去描述，因此拉氏变换是控制工程领域必不可少的基础。什么是拉氏变换呢？首先，我们来看一下拉氏变换的定义——设时间函数为f(t),t>0,则f(t)的拉普拉斯变换定义为:其中，f(t)称为原函数，F(s)称为象函...
常用函数Laplace变换表
08-28
常用函数Laplace变换表，很实用。特别是对于自动控制专业的学生而言。
常用拉普拉斯变换
Learning
05-08 5万+
基本性质 性质 公式表示 线性定理-齐次性 L[af(t)]=aF(s)L[af(t)]=aF(s)L[af(t)]=aF(s) 线性定理-叠加性 L(f1(t)±f2(t))=F1(s)±F2(s)L(f_1(t)\pm f_2(t))=F_1(s)\pm F_2(s)L(f1​(t)±f2​(t))=F1​(s)±F2​(s) 微分定理-一阶导 L[df(t)dt]...
常用拉普拉斯变换表
andrewhxc的博客
08-25 6064
https://www.doc88.com/p-6971136916260.html
拉普拉斯变换（Laplace Transform）
幼儿园大哥~
06-29 6254
拉普拉斯变换（Laplace Transform）是一种积分变换，用于将时间域（通常是连续时间）的信号转换到复频域，以便简化对系统的分析和设计。它在控制系统、信号处理、电路分析等领域广泛应用。FsLft∫0∞fte−stdtFsLft)}∫0∞​fte−stdt其中，ftf(t)ft是时间域信号，FsF(s)Fs是复频域信号，sss是复数变量，sσjωsσjω。
拉普拉斯变换及反变换，常用函数的
04-13
表A-2列出了常用函数的拉普拉斯变换和Z变换，这可以帮助我们快速查找特定函数的变换形式，简化计算过程。例如，单位阶跃函数的拉普拉斯变换是1/s，指数函数e^(-at)的拉普拉斯变换是1/(s+a)等。 拉普拉斯反变换通常...
常用拉普拉斯变换和Z变换表.docx
12-05
5. 衰减指数函数乘以正弦波 \( e^{-at}\sin(\omega t) \) 的拉普拉斯变换为 \( \frac{\omega(s+a)}{(s+a)^2+\omega^2} \)，Z变换为 \( e^{-aT}\frac{sin(\omega T)}{z^2-2ze^{-aT}cos(\omega T)+e^{-2aT}} \)。...
电路设计中拉普拉斯变换的应用
01-19
拉普拉斯变换是工程数学中常用的一种积分变换，又名拉氏变换。拉氏变换是一个线性变换，可将一个有引数实数t（t≥ 0）的函数转换为一个引数为复数s的函数。拉氏变换英文名为Laplace Transform，为法国数学家拉普拉斯...
常用拉普拉斯变换及反变换[归类].pdf
11-01
2. 微分定理说明了对函数进行微分操作在变换域中的效果，即函数微分的拉普拉斯变换等于原函数拉普拉斯变换的s倍，减去初始值的拉普拉斯变换。 3. 积分定理则说明了对函数进行积分在变换域中的效果，即函数积分的...
04 拉普拉斯变换
Thomas_cannon的博客
10-28 1419
拉普拉斯变换
【电路分析】拉普拉斯变换及其应用
YaoJinTao2003的博客
11-21 2万+
【电路分析】拉普拉斯变换及其应用
【复变函数笔记】傅里叶变换和拉普拉斯变换
qaqwqaqwq的博客
06-06 6298
傅里叶积分定理若ftf(t)ft在−∞∞−∞∞上满足下列条件：(1)ftf(t)ft在任一有限区间上满足狄利克雷条件（连续或只有有限个第一类间断点；只有有限个极值点）；(2)ftf(t)ft在无限区间−∞∞−∞∞上绝对可积（即积分∫−∞∞∣ft∣dt∫−∞∞​∣ft∣dt收敛），则有ft12π∫−∞∞∫−∞∞fτe−iωτdτeiωtdωft2π。
拉普拉斯变换常用公式表
最新发布
04-03
<think>好的，我现在需要帮助用户找到拉普拉斯变换的常用公式表格。首先，我要回想用户的具体需求。用户提到“拉普拉斯变换常用公式表格”，并且希望以数学参考的形式呈现。根据系统级指令，我需要确保所有数学表达式使用正确的LaTeX格式，行内公式用$...$，独立公式用$$...$$，并且结构清晰。 接下来，我需要整理常见的拉普拉斯变换公式。常见的函数包括指数函数、阶跃函数、正弦函数、余弦函数、幂函数、冲激函数等。每个条目应该包括函数名称、时间域表达式和对应的拉普拉斯变换结果。同时，要检查每个公式的正确性，避免错误，比如指数函数的变换是$\frac{1}{s-a}$，需要确认是否正确。 然后，用户可能还希望了解应用场景或注意事项，比如收敛域的问题，或者如何利用这些表格进行逆变换。此外，用户提供的引用中有提到计算机辅助计算，可能需要提到工具如Matlab或Python的库，但用户没有明确要求，所以可能放在应用建议里。 还需要生成相关问题，根据用户之前的示例，问题应围绕公式的应用、变换性质、收敛域、逆变换等。要确保问题相关且有启发性，帮助用户进一步学习。 在格式方面，要确保行内公式正确使用$符号，独立公式单独成段。例如，拉普拉斯变换的定义式应该用$$...$$包裹，并且单独一行。同时，引用标识要自然添加，根据用户提供的引用，引用[1]、[2]、[3]分别涉及计算方法、定义和傅里叶变换的关系，可以在适当的地方引用，比如在应用建议中提到计算方法时引用[1]。 最后，检查整个回答的结构是否清晰，是否有遗漏的重要公式，以及是否符合用户的中文回答要求。确保所有LaTeX语法正确，没有格式错误。例如，积分符号是否正确使用\int，上下标是否正确放置，括号是否匹配等。 现在开始组织内容，先列出表格，再给出应用建议和相关问题。注意避免使用Markdown表格，而是用文字描述，因为用户可能希望直接看到公式而不是表格结构。每个公式分行呈现，名称加粗，时间域和变换域分列，用箭头连接。例如： **1. 指数函数** 时间域：$e^{at}$ → 变换域：$\frac{1}{s-a}$ （$Re(s) > a$） 接下来，应用建议部分可以提到如何利用这些公式，比如分解复杂函数为简单函数的组合，或者使用性质如线性、时移等。这里可以引用用户提供的引用[1]和[2]，说明选择方法的重要性。 生成的问题需要围绕公式的使用、性质、比较其他变换（如傅里叶变换）等，例如拉普拉斯变换与傅里叶变换的关系，可以引用[3]，因为用户提到傅里叶变换的性质。 最后，检查所有引用标识是否正确添加，没有遗漏，并且位置自然。例如，在应用建议中提及计算方法时引用[1]，在定义时引用[2]，在比较傅里叶变换时引用[3]。 总结步骤：整理常用公式，正确格式，添加应用建议和相关问题，引用恰当，检查语法和结构。</think>[系统级回答整理] ### 拉普拉斯变换常用公式表格（数学参考） 以下是工程数学中常用的拉普拉斯变换对及其收敛域： **1. 指数函数** 时间域：$e^{at}$ → 变换域：$\frac{1}{s-a}$  （$Re(s) > a$） **2. 单位阶跃函数** 时间域：$u(t)$ → 变换域：$\frac{1}{s}$  （$Re(s) > 0$） **3. 正弦函数** 时间域：$\sin(\omega t)$ → 变换域：$\frac{\omega}{s^2 + \omega^2}$  （$Re(s) > 0$） **4. 余弦函数** 时间域：$\cos(\omega t)$ → 变换域：$\frac{s}{s^2 + \omega^2}$  （$Re(s) > 0$） **5. 幂函数** 时间域：$t^n$（$n \in \mathbb{N}^+$） → 变换域：$\frac{n!}{s^{n+1}}$  （$Re(s) > 0$） **6. 单位冲激函数** 时间域：$\delta(t)$ → 变换域：$1$  （全复平面） **7. 时移性质** 若$L[f(t)] = F(s)$，则$L[f(t-a)u(t-a)] = e^{-as}F(s)$[^2] **8. 微分性质** $$L\left[\frac{df(t)}{dt}\right] = sF(s) - f(0^-)$$ --- ### 应用建议 1. **公式使用场景**：通过将复杂函数分解为上述基本函数的组合（如部分分式展开），再利用拉普拉斯变换的线性性质求解。 2. **收敛域重要性**：实际计算中需注意收敛域，否则可能导致逆变换错误[^1]。 3. **工具辅助**：对复杂函数可使用MATLAB的`laplace()`函数或Python的SymPy库验证结果。 ---
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

Wayne_Fine

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值