1.基础知识
1.1 梯度 Hesse矩阵
1.2 二阶Taylor展开

1.3 极小点判定条件求无约束问题
驻点(一阶导=0)+ Hesse正定
1.4 凸函数判定
定理1.9 :f为c上的凸函数的充要条件是: ∇ 2 f ( x ) \nabla ^2 f(x) ∇2f(x) 在c上处处半正定
定理1.10:若f的 ∇ 2 f ( x ) \nabla ^2 f(x) ∇2f(x) 在C上处处正定,则f是C上的严格凸函数
注意: ∇ 2 f ( x ) \nabla ^2 f(x) ∇2f(x) 不好判断是否正定,则试试 − ∇ 2 f ( x ) -\nabla ^2 f(x) −∇2f(x)
凸规划:定义在凸集上的凸函数极小化问题
2.线性规划
2.1 线性规划问题
2.1.1 LP一般模型
目标函数:

约束条件:

标准形式


2.1.2 LP问题特征
线性规划问题的共同特征:
- 一组可控因素(决策变量)X表示一个方案,一般X大于等于0
- 约束条件是线性等式或不等式
- 目标函数是线性的。求目标函数最大化或最小化
2.2 线性规划解及其性质

设B是秩为m的约束矩阵A的一个 m阶满秩子方阵,则称B为一个基;B中 m 个线性无关的列向量称为基向量,变量 x中与之对应的m个分量称为基变量,其余的变量为非基变量,令所有的非基变量取值为0,得到的解 x = [ B − 1 , 0 ] T x=[B^{-1}, 0]^T x=[B−1,0]T称为相应于的基本解。 当 B − 1 b ≥ 0 当 B^{-1}b≥0 当B−1b≥0则称基本解为基本可行解,这时对应的基阵B为可行基。
如果 B − 1 b > 0 B^{-1}b>0 B−1b>0则称该基可行解为非退化的,如果一个线性规划的所有基可行解都是非退化的则称该规划为非退化的。

2.3 单纯形方法
思路:按照一种规则的方式,从一个顶点向相邻的一个顶点转换,直至找到一个最优解为止。
检验条件:对于任意的至少有一个最优解的LP,若一个顶点可行解没有更优的相邻顶点,则可行解一定是最优的。
基本思想:从方程组AX=b的某个基可行解开始(初试基可行解)在不违背条件X≥0的前提下,不断生成新的基可行解(相邻的基可行解),且基可行解的每次更新,均能确保目标函数值有所改进,一直到获得最优解为止,是一个多次迭代的过程。
求解线性规划问题的基本思路:
- 构造初始可行基
- 求出一个基本可行解(顶点)
- 最优性检验:判断是否为最优解
- 基变换,转2.要保证目标函数值比原来更优
2.3.1 单纯形表
检验数:
- ≤ 0时,最优解
-
0时,无解;换基,继续
基变换:
- 换入变量:选最大非负检验数对应的变量
- 换出变量:选非负 θ i \theta_i θi的最小者对应的变量换出; θ = m i n { b 1 ′ a 12 ′ , b 2 ′ a 22 ′ , b 3 ′ a 32 ′ ∣ a k 2 ′ > 0 } \theta = min~\{\frac{b_1'}{a_{12}'}, \frac{b_2'}{a_{22}'}, \frac{b_3'}{a_{32}'} | a_{k2}' > 0\} θ=min {a12′b1′,a22′b2′,a32′b3′∣ak2′>0}



2.3.2 最优性检验与解的判别
最优解判别定理
若 X = ( b 1 ′ , b 2 ′ , . . . , b m ′ , 0 , . . . , 0 ) T X=(b_1', b_2', ..., b_m', 0, ..., 0)^T X=(b1′,b2′,...,bm′,0,...,0)T为基可行解,且全部 σ j ≤ 0 , j = m + 1 , . . . , n \sigma_j≤0, j=m+1, ..., n σj≤0,j=m+1,...,n,则X为最优解
无穷多最优解的判定
当所有的 σ j ≤ 0 \sigma_j≤0 σj≤0,又对某个非基变量 x k ′ x_k' xk′,有 σ k = 0 \sigma_k=0 σk=0,则该线性规划问题有无穷多最优解,只需将 x k x_k xk换入基变量中,找到一个新的基可行解 x ( 1 ) x^{(1)} x(1),因为 σ k = 0 \sigma_k=0 σk=0由此知道 Z = Z 0 Z=Z_0 Z=Z0,表明可以找到另一个顶点目标函数值也达到最大,由于两点连线上的点也属于可行域,并且目标函数值相等,即该线性规划问题有无穷多最优解。
无最优解的判定
X = ( b 1 ′ , b 2 ′ , . . . , b m ′ , 0 , . . . , 0 ) T X=(b_1', b_2', ..., b_m', 0, ..., 0)^T X=(b1′,b2′,...,bm′,0,...,0)T为基可行解,如果存在 σ m + k = 0 \sigma_{m+k}=0 σm+k=0又 P m + k P_{m+k} Pm+k向量的所有分量 a i , m + k ≤ 0 ( i = 1 , 2 , . . . , m ) a_{i, m+k} ≤0 (i=1,2,...,m) ai,m+k≤0(i=1,2,...,m),这时线性规划问题存在无界解
2.4大M方法
“惩罚”人工变量

- 大M法实质上与原单纯形法一样,M可看成一个很大的常数
- 人工变量被迭代出去后一般就不会再成为基变量
- 当检验数都满足最优条件,但基变量中仍有人工变量,说明原线性规划问题无可行解
- 大M法手算很不方便
- 因此提出了两阶段法
- 计算机中常用大M法
- 两阶段法手算可能容易
2.5 两阶段法
2.5.1 步骤
第一阶段:构造如下的线性规划问题

- 目标函数仅含人工变量,并要求实现最小化。若其最优解的目标函数值不为0,也即最优解的基变量中含有非零的人工变量,则原线性规划问题无可行解。
- 人工变量的系数矩阵为单位矩阵,可构成初始可行基。
用单纯形法求解上述问题,若 ω = 0 ω=0 ω=0,进入第二阶段,否则,原问题无可行解。
第二阶段:去掉人工变量,还原目标函数系数,做出初始单纯形表
用单纯形法求解即可。
2.5.2 思想
- 第一阶段的任务是将人工变量尽快迭代出去,从而找到一个没有人工变量的基本可行解
- 第二阶段以第一阶段得到的基本可行解为初始解,采用原单纯形法求解
- 若第一阶段结束时,人工变量仍在基变量中,则原问题无解
- 为了简化计算,在第一阶段重新定义价值系数如下

2.5.3 解的退化
计算出的 θ θ θ(用于确定换出变量)存在有两个以上相同的最小比值,会造成下一次迭代中有一个或几个基变量等于零,这就是退化(会产生退化解)。
可能出现以下情况:
- 进行进基、出基变换后,虽然改变了基,但没有改变基本可行解(极点),目标函数当然也不会改进。进行若干次基变换后,才脱离退化基本可行解(极点),进入其他基本可行解(极点)。这种情况会增加迭代次数,使单纯形法收敛的速度减慢。
- 在特殊情况下,退化会出现基的循环。一旦出现这样的情况,单纯形迭代将永远停留在同一极点上,因而无法求得最优解。
在单纯形法求解线性规划问题时,一旦出现这种因退化而导致的基的循环,单纯形法就无法求得最优解,这是一般单纯形法的一个缺陷。但是实际上,尽管退化的结构是经常遇到的,而循环现象在实际问题中出现得较少。
1976年,Bland提出了一个避免循环的新方法,其原则十分简单:
- 当 σ j \sigma_j σj中出现两个以上最大值时,选下标最小的非基变量为换入变量;
- 当 θ θ θ中出现两个以上最小值时,选下标最小的基变量为换出变量。
这样就可以避免出现循环,当然,这样可能使收敛速度降低。
2.6LP小结

2.7 对偶


3.无约束最优化问题
3.1 直线搜索
3.2 最速下降法
最速下降法是最早的求解多元函数极值的数值方法。它直观、简单。它的缺点是,收敛速度较慢、实用性差。
算法描述
迭代公式: x k + 1 = x k + t k p k x_{k+1}=x_k + t_k p_k xk+1=xk+tkpk
搜索方向:$p_k=-\nabla f(x_k) $ 负梯度方向
步长:
- ∇ 2 f ( x ) \nabla^2f(x) ∇2f(x)非正定:含 t k t_k tk的 x k + 1 x_{k+1} xk+1代入 f ( x ) f(x) f(x) 得 φ ( t k ) \varphi(t_k) φ(tk),求导为0,得出 t k t_k tk
- ∇ 2 f ( x ) \nabla^2f(x) ∇2f(x)正定: t k = g k T g k g k T Q g k t_k=\frac{g_k^T g_k}{g_k^T Q g_k} tk=gkTQgkgkTgk
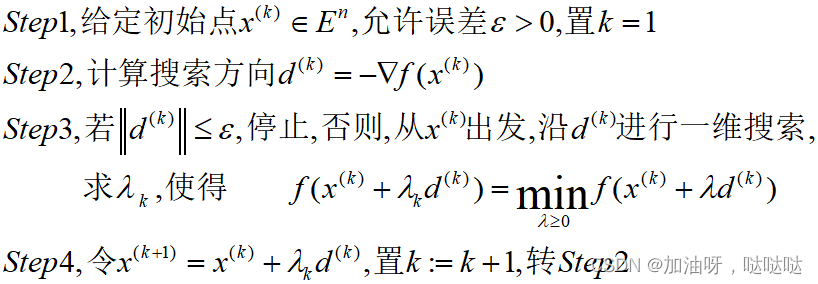
锯齿现象
最速下降法的迭代点在向极小点靠近的过程中,走的是曲折的路线:后一次搜索方向 P k + 1 P_{k+1} Pk+1与前一次搜索方向 P k P_k Pk总是相互垂直的,称它为锯齿现象。这一点在前面的例题中已得到验证。除极特殊的目标函数(如等值面为球面的函数)
和极特殊的初始点外,这种现象一般都要发生。

从直观上可以看到,在远离极小点的地方,每次迭代都有可能使目标函数值有较多的下降,但在接近极小点的地方,由于锯齿现象,每次迭代行进的距离开始逐渐变小。因而收敛速度不快。
已有结论表明,最速下降法对于正定二次函数关于任意初始点都是收敛的,而且恰好是线性收敛的。
算法特点
- 全局收敛
- 线性收敛
- 算法比较简答
- 开始迭代好,靠近最优解时有扭摆现象
3.3 Newton法
如果目标函数 f ( x ) f(x) f(x)在 R n R^n Rn上具有连续的二阶偏导数,其Hesse矩阵正定且可以表达成显式,那么使用 Newton法求解(3.1)会很快地得到极小点。
迭代公式:
x k + 1 = x k − G k − 1 g k x_{k+1}=x_k - G_k^{-1} g_k xk+1=xk−Gk−1gk
搜索方向: p k = − G k − 1 g k p_k=-G_k^{-1} g_k pk=−Gk−1gk
步长因子为1
修正Newton法:newton法失败
- Hesse矩阵 ∣ G k ∣ = 0 |G_k|=0 ∣Gk∣=0,取 p k = − g k p_k = -g_k pk=−gk,做直线搜索, x k + 1 = l s ( x k , p k ) x_{k+1} = ls(x_k, p_k) xk+1=ls(xk,pk)
- Hesse矩阵
∣
G
k
∣
≠
0
|G_k| ≠ 0
∣Gk∣=0,取
p
k
=
−
G
k
−
1
g
k
p_k = -G_k^{-1}g_k
pk=−Gk−1gk →
x
k
+
1
=
x
k
+
p
k
x_{k+1}=x_k+p_k
xk+1=xk+pk
- f ( x k + 1 ) < f ( x k ) f(x_{k+1}) < f(x_k) f(xk+1)<f(xk) :有效迭代
- $f(x_{k+1}) ≥ f(x_k) $:无效迭代
3.4 共轭方向法与共轭梯度法
共轭方向法是介于最速下降法和Newton法之间的一种方法,它克服了最速下降法的锯齿现象,从而提高了收敛速度;它的迭代公式也比较简单,不必计算目标函数的二阶导数,与Newton法相比,减少了计算量和存储量。它是比较实用而有效的最优化方法。
3.4.1 基本思想
归纳一下,对于二元二次目标函数,从任意初始点 x 0 x_0 x0出发,沿任意下降方向 P 0 P_0 P0做直线搜索得到 x 1 x_1 x1;再从 x 1 x_1 x1出发,沿 P 0 P_0 P0的共轭方向 P 1 P_1 P1(可由 P 1 = − ∇ f ( x 1 ) + P 0 T ∇ f ( x 1 ) P 0 T Q P 0 P 0 P_1=-\nabla f(x_1)+\frac{P_0^T \nabla f(x_1)}{P_0^TQP_0} P_0 P1=−∇f(x1)+P0TQP0P0T∇f(x1)P0确定)作直线搜索,所得到的必是极小点 x ∗ x^* x∗。
上面的结果可以推广到n维空间中,即在n维空间中,可以找出N个互相共轭的方向,对于n元正定二次函数,从任意初始点出发,顺次沿着这n个共轭方向最多作n次直线搜索,就可以求到目标函数的极小点。
对于n元正定二次目标函数,如果从任意初始点出发经过有限次迭代就能够求到极小点,那么称这种算法具有二次终止性。例如,Newton法对于二次函数只须经过一次迭代就可以求到极小点,因此是二次终止的;而最速下降法就不具有二次终止性。共轭方向法(如共轭梯度法、拟Newton 法等)也是二次终止的。一般说来,具有二次终止性的算法,在用于一般函数时,收敛速度是较快的。
3.4.2 共轭向量及其性质
3.4.3 共轭方向法
3.4.4 共轭梯度法
(1)第1个迭代点得获得:最速下降法
迭代公式: x 1 = x 0 + t 0 p 0 x_1 = x_0 + t_0 p_0 x1=x0+t0p0
迭代方向: p 0 = − g 0 p_0 = -g_0 p0=−g0
步长因子: t 0 = − p 0 T g 0 p 0 T Q p 0 = g 0 T g 0 p 0 Q p 0 t_0 = - \frac{p_0^T g_0}{p_0^TQp_0}=\frac{g_0^Tg_0}{p_0 Q p_0} t0=−p0TQp0p0Tg0=p0Qp0g0Tg0
(2)后续迭代点
迭代公式: x k + 1 = x k + t k p k x_{k+1} = x_k + t_k p_k xk+1=xk+tkpk
迭代方向: p k = − g k + α k p k − 1 p_k = - g_k + \alpha_k p_{k-1} pk=−gk+αkpk−1
步长因子: t k = − p k T g k p k T Q p k = g k T g k p k Q p k t_k = - \frac{p_k^T g_k}{p_k^TQp_k}=\frac{g_k^Tg_k}{p_k Q p_k} tk=−pkTQpkpkTgk=pkQpkgkTgk
(3)F-R共轭梯度
α k = g k + 1 T g k + 1 g k T g k = ∣ ∣ g k + 1 ∣ ∣ 2 ∣ ∣ g k ∣ ∣ 2 \alpha_k = \frac{g_{k+1}^Tg_{k+1}}{g_k^Tg_k} = \frac{||g_{k+1}||^2}{||g_k||^2} αk=gkTgkgk+1Tgk+1=∣∣gk∣∣2∣∣gk+1∣∣2
(4)总结
实际上,可以把共轭梯度法当作最速下降法的一种改进方法,因为当令所有的$ \alpha_k=0$时,它就变为最速下降法。共轭梯度法的效果不低于最速下降法。共轭梯度法是收敛的算法。
共轭梯度法还有一个优点,就是存储量小。因为它不涉及矩阵,仅仅存放向量就够了,因此适用于维数较高的最优化问题。
共轭梯度不要求精确的直线搜索,这也是一个优点。但是,不精确的直线搜索可能导致迭代出来向量不再共轭,从而有可能不再线性无关,这将降低方法的效能。克服的办法是,重设初始点,即把经过n+1次迭代后得到的 x n + 1 x_{n+1} xn+1作为初始点,再开始新一轮的迭代。计算实践指出,用 x n + 1 x_{n+1} xn+1比用 x n x_n xn作初始点要好。
3.5 拟Newton法
Newton法的优缺点都很突出。优点:高收敛速度(二阶收敛);缺点:对初始点、目标函数要求高,计算量、存储量大(需要计算、存储Hesse矩阵及其逆)。拟Newton法是模拟Newton法给出的一个保优去劣的算法。
拟Newton法是效果很好的一大类方法。它当中的 DFP算法和 BFGS算法是直到目前为止在不用Hesse矩阵的方法中的最好方法。
3.5.1 基本思想

3.5.2 DFP算法
DFP法是首先由Davidon (1959年)提出,后由Fletcher和 Powell (1963年)改进的算法。它是无约束优化方法中最有效的方法之一。DFP法虽说比共轭梯度法有效,但它对直线搜索有很高的精度要求。
校正公式


3.6 步长加速法
步长加速法是由Hooke和 Jeeves ( 1961年)给出的一种直接方法。对于变量数目较少的无约束极小化问题,这是一个程序简单又比较有效的方法。
3.6.1 基本思想
步长加速法主要由交替进行的“探测搜索”和“模式移动”组成。前者是为了寻找当前迭代点的下降方向,而后者则是沿着这个有利的方向寻求新的迭代点。
“Ⅰ型探测”:出发点既是参考点,又是基点,目的是在基点周围构造一个模式;
“Ⅱ型探测”:出发点是参考点,目的是判别上次得模式移动是否成功,从而能否做加速移动。
给出初始点 x 0 x_0 x0,以它作为探测搜索的出发点(称为参考点,用 r r r表示,即 r = x 0 r=x_0 r=x0。),在其周围寻找比它更好的 b b b点(称为基点),即 f ( b ) < f ( r ) f(b)<f(r) f(b)<f(r),以得到下降方向 b − r b-r b−r (称为模式)。然后从 b b b出发沿模式 b − r b-r b−r做直线搜索(称为模式移动).
3.6.2 算法
(1)探测算法
已知:目标函数 f ( x ) f(x) f(x),步长向量 s = [ s 1 , s 2 , . . . , s n ] T s=[s_1, s_2, ..., s_n]^T s=[s1,s2,...,sn]T,参考点 r = [ r 1 , r 2 , . . . , r n ] T r=[r_1, r_2, ..., r_n]^T r=[r1,r2,...,rn]T.
- 计算 f r = f ( r ) f_r=f(r) fr=f(r);置 b = r b=r b=r, f b = f r f_b=f_r fb=fr
- 一次沿第 i = 1 , 2 , . . . , n i=1,2,...,n i=1,2,...,n个坐标轴方向做直线搜索;计算 f 1 = f ( b + s i e i ) f_1=f(b+s_i e_i) f1=f(b+siei), f 2 = f ( b − s i e i ) f_2=f(b-s_i e_i) f2=f(b−siei)
则有以下三种情况:
- 若 f 1 < f b f_1<f_b f1<fb,则置 b = b + s i e i b=b+s_i e_i b=b+siei, f b = f 1 f_b=f_1 fb=f1
- 若 f 2 < f b < f 1 f_2<f_b<f_1 f2<fb<f1,则置 b = b − s i e i b=b-s_i e_i b=b−siei, f b = f 2 f_b=f_2 fb=f2
- 若 f 1 ≥ f b f_1≥f_b f1≥fb, f 2 ≥ f b f_2≥ f_b f2≥fb,则 b b b与 f b f_b fb不变
依次对i=1,2,…,n计算后,最终的b是从r出发以s为步长向量探测搜索的终点。
当 f b < f r f_b < f_r fb<fr时,探测搜索称为成功,此时必有b≠r,即得到模式b-r;否则,探测搜索称为失败,此时未得到模式。
(2)步长加速法
已知:目标函数 f ( x ) f(x) f(x),步长收缩系数的终止限 ϵ \epsilon ϵ
- 选定初始点 x 0 x_0 x0,初试步长量为 s 0 s_0 s0,置 r = x 0 r=x_0 r=x0, b 0 = x 0 b_0=x_0 b0=x0, c = 1 c=1 c=1, w = 0.5 w=0.5 w=0.5
- 置 s = c s 0 s=cs_0 s=cs0
- 在点 r r r处,以 s s s为步长向量按探测算法做探测搜索得 b b b
- 若 f ( b ) < f ( r ) f(b) < f(r) f(b)<f(r),则转5,否则转8
- 做模式移动 r = 2 b − b 0 r=2b-b_0 r=2b−b0,并置 b 0 = b b_0=b b0=b, f 0 = f f_0=f f0=f
- 在点 r r r处,以 s s s为步长向量按 探测算法 做探测搜索得 b b b
- 若 f ( b ) < f ( b 0 ) f(b) < f(b_0) f(b)<f(b0),则转5;否则,置 r = b 0 r=b_0 r=b0,转3
- 若 c ≤ ϵ c ≤ \epsilon c≤ϵ ,则输出r,停止计算;否则,置 c = w c c=wc c=wc,转2
3.6.3 算法特点
-
步长加速法的收敛速度是线性的,如果目标函数可微,则可收敛到平稳点;
-
可用于任何形式的目标函数;
-
收敛速度比较慢,但是编制程序比较简单,而且可靠。
3.7 最小二乘法
3.7.1 引言
在数据处理中经常遇到寻求回归方程的问题,即根据一组实验数据建立两个或多个物理量(俗称因素)之间的在统计意义上的依赖关系式。这类问题的一般性描述如下。
把平方和作为实验点到曲面的总距离的度量,并且使其取极小值来确定方程中参数,这种方法就是著名的最小二乘法。
设 x = [ x 1 , x 2 , . . . , x n ] T x=[x_1, x_2, ..., x_n]^T x=[x1,x2,...,xn]T, t i = [ t 1 i , t 2 i , . . . , t l i ] t^{i}=[t_1^{i}, t_2^{i}, ..., t_l^{i}] ti=[t1i,t2i,...,tli],则上述最小二乘问题可简写为: m i n ∑ i = 1 m [ F ( t ( i ) , x ) − y ( i ) ] 2 min \sum_{i=1}^m[F(t^{(i)},x) - y^{(i)}]^2 min∑i=1m[F(t(i),x)−y(i)]2
最小二乘问题的一般形式: m i n ∣ ∣ F ( x ) − y ∣ ∣ 2 min ~ || F(x) - y ||^2 min ∣∣F(x)−y∣∣2 或 m i n f ( x ) T f ( x ) min ~ f(x)^Tf(x) min f(x)Tf(x)
3.7.2 最小二乘问题解法:线性
当 f ( x ) f(x) f(x)取线性函数形式,即$ f(x)=A(x)+b$时,其中A是 m × n m\times n m×n矩阵,b是m维向量,可表示为:$ min ~ ||Ax-b||^2$,称为线性最小二乘问题。
一些定理:
- x ∗ x^* x∗是最小二乘的极小点的充要条件是 x ∗ x^* x∗是方程组 A T A x = A T b A^TAx=A^Tb ATAx=ATb的解
- 设A是 m × n m\times n m×n矩阵(m≥n),则 A T A A^TA ATA正定的充要条件是A的秩为n。
- 当A的秩为n时, x = ( A T A ) − 1 A T b x=(A^TA)^{-1}A^Tb x=(ATA)−1ATb是方程唯一的最小二乘解
4.约束最优化问题
约束最优化问题常用的两类最优化方法。
- 容许方向法:一种直接处理约束的方法
- 罚函数法:一种直接处理约束问题本身的方法
其主要特点是用一系列无约束问题的极小点去逼近约束问题的最优点
4.1最优性条件
所谓最优性条件,就是最优化问题的目标函数与约束函数在最优点所满足的充分条件和必要条件。
最优性必要条件是指,最优点应该满足的条件;
最优性充分条件是指,可使得某个容许点成为最优点的条件。
最优性条件对于最优化算法的终止判定和最优化理论的推证都是至关重要的。
4.1.1 等式约束问题的最优性条件
考虑仅含等式约束的问题:

Lagrange定理 和Lagrange乘子法
Lagrange定理:求解等式约束问题等价于求解无约束问题,其中$ \lambda_1, \lambda_2, …, \lambda_l $称为Lagrange乘子

求解最优值:对x, λ \lambda λ求偏导,若使$ \nabla^2 L(x)$ 正定,则 x为最优点
4.1.2 不等式约束问题的最优性条件
(1)几何最优性条件
约束问题:

设容许集用D表示,即 D = { x ∣ s i ( x ) ≥ 0 , i = 1 , 2 , . . . , m } D=\{x | s_i(x) ≥ 0, i=1,2,...,m\} D={x∣si(x)≥0,i=1,2,...,m}
(不)起作用约束
若x使得某个不等式约束有 s i ( x ) = 0 s_i(x)=0 si(x)=0,则该不等式约束 s i ( x ) ≥ 0 s_i(x)≥0 si(x)≥0称为关于容许点 x x x的起作用约束;否则,若 s i ( x ) > 0 s_i(x)>0 si(x)>0,则该不等式约束称为是关于容许点 x x x的不起作用约束。

不等式约束关于容许集的任意内点都是不起作用约束。只有容许集的边界点才能使某个或某些不等式约束变为起作用约束。
下降方向锥
几何最优条件
定理:在上述约束问题种,若 x ∗ x^* x∗是局部最优点,则点 x ∗ x^* x∗处的容许方向锥和下降方向锥的交集为空集。即在最优点 x ∗ x^* x∗处,一定不存在下降容许方向
几何解释
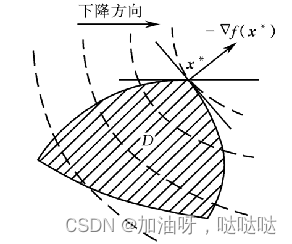
假设:
- x ∗ x^* x∗是局部最优点, I = { i ∣ s i ( x ∗ ) = 0 , i = 1 , 2 , . . . , m } I=\{i|s_i(x^*)=0, i=1,2,...,m\} I={i∣si(x∗)=0,i=1,2,...,m}
- f(x)在点 x ∗ x^* x∗处可微;当 i ∈ I i\in I i∈I时, s i ( x ) s_i(x) si(x)在点 x ∗ c x^*c x∗c处可微;当 i ∉ I i \notin I i∈/I时, s i ( x ) s_i(x) si(x)在点 x ∗ x^* x∗处连续
G ( x ∗ ) ∩ S ( x ∗ ) = ∅ G(x^*) \cap S(x^*) = \emptyset G(x∗)∩S(x∗)=∅,其中, G = { ∇ f ( x ) T p < 0 } G=\{\nabla f(x)^T p < 0\} G={∇f(x)Tp<0}, S = { ∇ S ( x ) T p > 0 } S=\{\nabla S(x)^T p > 0\} S={∇S(x)Tp>0}
(2)F-J条件
在有约束最优化问题中,设 x ∗ x^* x∗是局部最优解, f ( x ) f(x) f(x), s 1 ( x ) s_1(x) s1(x), s 2 ( x ) s_2(x) s2(x), …, s m ( x ) s_m(x) sm(x)在点 x ∗ x^* x∗处可微。那么,存在不全为零的实数 u 0 , u 2 , . . . , u m u_0, u_2, ..., u_m u0,u2,...,um,使得

其中, u i s i ( x ∗ ) = 0 u_is_i(x^*)=0 uisi(x∗)=0称为互补松弛条件。若 s i ( x ∗ ) > 0 s_i(x^*)>0 si(x∗)>0,即 i ∉ I i \notin I i∈/I,则必有 u i = 0 u_i=0 ui=0;若 u i > 0 u_i>0 ui>0,则必有 s i ( x ∗ ) = 0 s_i(x^*)=0 si(x∗)=0,即 i ∈ I i\in I i∈I
F-J条件仅是判断容许点是否为最优点的必要条件,而不是充分条件
(3)K-T条件
总结:Fritz-John条件失效的一个原因是,起作用约束函数的梯度线性相关。为保证 ∇ f ( x ∗ ) \nabla f(x^*) ∇f(x∗)一定在Fritz-John条件中出现,即必须保证 u 0 > 0 u_0 >0 u0>0,这可以通过附加上起作用约束函数的梯度线性无关的条件——Kuhn和 Tucker提出的条件。
K-T条件
在起作用约束函数的梯度线性无关的前提下,下列公式称为K-T条件

Kuhn-Tucker条件的几何意义:在公式中,删去不起作用约束项(注意,它们的系数是 u i = 0 ( i ∉ I ) u_i=0(i\notin I) ui=0(i∈/I) ),
K-T条件可简写为:存在 u i ≥ 0 ( i ∈ I ) u_i≥0(i \in I) ui≥0(i∈I),使得$ \nabla f(x^) = \sum_{i \in I} u_i \nabla s_i(x^)$.
K-T条件时F-J条件的特殊情况。
4.1.3 一般约束问题的最优性条件
若 x ∗ x^* x∗时一般约束问题的K-T点,则 x ∗ x^* x∗是全局最优点。
4.2 Z容许方向法
容许方向法是沿着下降容许方向搜索并保持新迭代点为容许点的一种迭代方法。下降容许方向确定方法的不同对应着不同的容许方向法。
第一,Zoutendijk容许方向法。这种方法通过在迭代点处的容许方向锥中寻找最速下降方向的线性规划来确定下降容许方向。
第二,Rosen梯度投影法。该法通过把在迭代点处的目标函数的负梯度向起作用约束超平面的交集投影来确定下降容许方向。
4.2.1 线性约束的情形
考虑线性约束最优化问题:

其中:A是 m × n m\times n m×n矩阵,C是 l × n l\times n l×n矩阵, b b b是 m m m维向量, d d d是 l l l维向量。
(1)下降容许方向的确定
书中,定理4.14,假设:
- x是容许点
- 适当调换A的行向量与b的向量分量(设所得矩阵和向量仍用A与b表示),然后分解 A = [ A ′ , A ′ ′ ] A=[A', A''] A=[A′,A′′],相应的分解 b = [ b ′ , b ′ ′ ] b=[b', b''] b=[b′,b′′],使得 A ′ x = b ′ A'x=b' A′x=b′, A ′ ′ x > b ′ ′ A''x>b'' A′′x>b′′
那么,非零向量p为点x的容许方向的充要条件是p满足: A ′ p ≥ 0 A'p≥0 A′p≥0, C p = 0 Cp=0 Cp=0
为了确定点x的下降容许方向向量p,一个很自然的想法就是,在满足 A ′ p ≥ 0 A'p≥0 A′p≥0, C p = 0 Cp=0 Cp=0的条件下,使 ∇ f ( x ) T p \nabla f(x)^Tp ∇f(x)Tp取极小值
综上,考虑如下极小化问题:

注意到这是具有非线性约束的问题,考虑用相近的线性规划

用上述方程来确定在点x处的下降容许方向向量,其中 e e e是分量全为1的n维向量,即 e = [ 1 , 1 , . . . , 1 ] T e=[1,1,...,1]^T e=[1,1,...,1]T。
若最优值为负,则最优解 p ∗ p^* p∗就是点x的一个下降容许方向向量。
(2)直线搜索
为求新的迭代点 x 1 x_1 x1,以从点x出发,沿下降容许方向p做直线搜索。
容许区间:

最优步长因子 t ∗ t^* t∗是如下一元函数极小化问题的最优解:
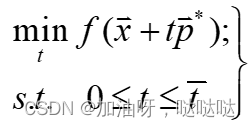
其中:

(3)终止准则
x为K-T点的充要条件是:
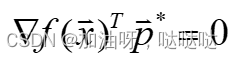
4.3 外部罚函数法
罚函数法。它的特点是根据问题的约束函数和目标函数,构造一个具有“惩罚”效果的目标函数序列,从而把对约束最优化问题的求解转化为对一系列无约束问题的求解。这种“惩罚”策略,对在无约束问题求解过程中企图违反约束的那些迭代点给予很大的目标函数值,迫使这一系列无约束问题的极小点(即迭代点)或者无限地向容许集靠近,或者一直保持在容许集内,直.到收敛到约束问题的极小点。
外部罚函数法(外点法):其惩罚方式是对那些违反约束的点在目标函数中加入相应的“惩罚”,而对容许点不予惩罚。特点是迭代点一般在容许集外移动。
内部罚函数法(内点法):它仅适用于具有不等式约束的最优化问题。其惩罚方式是对那些企图从内部穿越容许集边界的点(容许集的内点)在目标函数中加入相应的“障碍”,而且点距边界越近,障碍也越大,对于边界上的点给予无穷大的障碍,从而保证迭代点一直在容许集内移动。三是乘子法,它是外部罚函数法的一种改进方法。
4.3.1 算法的构成
(1)等式约束
等式约束:仅含有等式约束的问题

惩罚策略:
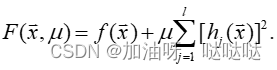
(2)不等式约束
不等式约束:仅含不等式约束问题

惩罚策略:

其中u是阶跃函数,
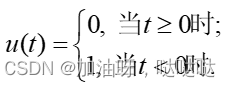
(3)一般约束问题

其中:

显然有:

这里的D是容许集。
此外, F ( x , u ) F(x,u) F(x,u)称为约束问题的增广目标函数,其中的 u u u称为罚因子, u α ( x ) u\alpha (x) uα(x)称为惩罚项
于是,约束优化问题转化为无约束优化问题。
定理4.22指出,当 u u u固定时,无约束问题的极小点有可能是约束问题的极小点,充要条件为 x u x_u xu为容许点。
在实际的算法中,把 u u u取为一个趋于正无穷大的正数序列 { u k } \{u_k\} {uk},并对 k = 0 , 1 , 2. … k=0,1,2.… k=0,1,2.…,依次求解无约束问题,由此得到极小点序列 { x k } \{x_k\} {xk}。如果这个序列收敛,则必收敛于约束问题的极小点”。这种通过求解一系列无约束问题而达到求解无约束问题的方法称为外部罚函数法或外点法。
4.4 内部罚函数法
内部罚函数法的初始点必须是容许点,迭代点在容许集的内部移动。
基本想法是,对越接近容许集边界的(容许)点施加越大的惩罚,对边界上的点干脆施加无穷大的惩罚。这好比在容许集的边界上筑就了一道高墙,阻碍迭代点穿越边界,把迭代点封闭在容许集内。
这个想法,内部罚函数法就仅适用于具有不等式约束的问题,而且容许集的内点集合必须是非空集合;否则,会因为容许点全被加上无穷大的惩罚而失去惩罚的意义。
4.4.1 算法的构成
考虑不等式约束问题:

构造如下目标函数:
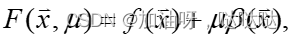
其中:

F ( x , u ) F(x,u) F(x,u)称为障碍函数; u ( > 0 ) u(>0) u(>0)称为罚因子; u β ( x ) u\beta (x) uβ(x)称为惩罚项。若x是容许集D的内点,则障碍函数 β ( x ) \beta(x) β(x)的值是有限的正数;当x由内部接近边界时,则至少有一个约束函数, s i ( x ) s_i(x) si(x)将趋于零,于是 β ( x ) \beta(x) β(x)必将趋于正无穷大。
现在固定 u u u,求解目标函数的无约束问题: m i n F ( x , u ) min ~ F(x, u) min F(x,u),如果把初始点取为容许集D的内点,按照F的结构和无约束下降迭代算法的特性,那么迭代点必将都在D内,因此最后求得的极小点也必将属于D。
在实际的算法中,把 u u u取为一个趋于零的正数序列 { u k } \{u_k\} {uk},求解一系列无约束问题,即对 k = 0 , 1 … k =0,1… k=0,1…,依次求解。由此得到极小点序列 { k } \{k\} {k}。若这个序列若收敛,则必收敛于约束问题的极小点 x ∗ x^* x∗。这种通过求解一系列无约束问题而达到求解约束问题的方法称为内部罚函数法或内点法。
4.5 乘子法
乘子法是针对外部罚函数法的一种改进方法。
由于外部罚函数法随着罚因子的增大,增广目标函数的Hesse矩阵条件数变得越来越坏,从而导致在实际计算中,数值计算的稳定性变得越来越差,难以精确求解。
乘子法是在约束问题的Lagrange函数中加入相应的惩罚,使得在求解系列无约束问题时,罚因子不必趋于无穷大就能求到约束问题的最优解,而且数值计算的稳定性也能得到很好的保证。理论与计算实践皆表明,乘子法优于外部罚函数法。
4.5.1 等式约束
考虑等式约束问题,写为向量形式:

其中 f f f,$ h 都是二次连续可微函数。设 都是二次连续可微函数。设 都是二次连续可微函数。设D={x|h(x)=0}$
原约束问题的Lagrange函数是: L ( x , λ ) = f ( x ) − λ T h ( x ) L(x,\lambda)=f(x)-\lambda^Th(x) L(x,λ)=f(x)−λTh(x)
原约束问题可等价于:
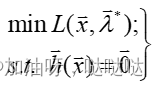
对上述使用外部罚函数法,则增广目标函数为:

注意到, λ ∗ \lambda^* λ∗其实是未知变量,所以实际上不能求出 F ( x , λ ∗ , u ) F(x,\lambda^*,u) F(x,λ∗,u)的极小点;实际上,可使用迭代的方法求解 x ∗ x^* x∗,$ \lambda^*$.
实际上,用乘子法求解的增广目标函数如下:

定理:对于给定的参数 λ \lambda λ 和 u u u, x ∗ x^* x∗是乘子法求解的增广目标函数的最优解。那么也是原优化问题的最优解的充要条件是 h ( x ) = 0 h(x)=0 h(x)=0,即 x ∈ D x\in D x∈D
采用如下的迭代公式求$ \lambda^*$:

当$||h(x_k)|| 充分小时,迭代终止。而一旦在迭代中 充分小时,迭代终止。而一旦在迭代中 充分小时,迭代终止。而一旦在迭代中{\lambda_k} 不收敛或收敛太慢,这表明 不收敛或收敛太慢,这表明 不收敛或收敛太慢,这表明u 不够大,因此增大 不够大,因此增大 不够大,因此增大u 后,在迭代。收敛的快慢,可用比值 后,在迭代。收敛的快慢,可用比值 后,在迭代。收敛的快慢,可用比值\frac{h(x_k)}{h(x_{k-1})}$来衡量
4.5.2 不等式约束
这里将要介绍的是Rockafellar( 1973)乘子法,它是把H乘子法巧妙地用到不等式约束问题上去而得到的求解仅含不等式约束问题的一种方法。
考虑不等式约束问题:

增广目标函数:

对于给定参数的 v = v k v=v_k v=vk和 u u u,设 x k x_k xk, z k z_k zk是 m i n x , z F ( x , z , v k , u ) min_{x,z}~F(x,z,v_k,u) minx,z F(x,z,vk,u)的极小点,并定义 z k 2 = [ z 1 2 , z 2 2 , . . . , z m 2 ] T z_k^2=[z_1^2, z_2^2, ..., z_m^2]^T zk2=[z12,z22,...,zm2]T,则乘子的迭代公式为:

终止准则为:

4.5.3 一般约束
对于一般约束问题:

增广目标函数:

乘子的迭代公式:

其中 λ j \lambda_j λj代表的是第j 个等式约束所对应的Lagrange乘子, v i v_i vi代表的是第i个不等式约束对应的 Lagrange乘子,显然 v i ≥ 0 v_i≥0 vi≥0。







 文章介绍了数学优化中的关键概念和方法,包括线性规划的原理、最速下降法、Newton法、共轭梯度法以及无约束最优化问题的解决策略。特别讨论了如何判断极小点、凸函数的性质以及各种算法的优缺点,如线性规划的单纯形法、大M法、步长加速法和最小二乘法。此外,还提到了约束最优化问题的Kuhn-Tucker条件和乘子法的应用。
文章介绍了数学优化中的关键概念和方法,包括线性规划的原理、最速下降法、Newton法、共轭梯度法以及无约束最优化问题的解决策略。特别讨论了如何判断极小点、凸函数的性质以及各种算法的优缺点,如线性规划的单纯形法、大M法、步长加速法和最小二乘法。此外,还提到了约束最优化问题的Kuhn-Tucker条件和乘子法的应用。
















 4376
4376

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








