关联线探究，如何连接流程图的两个节点

如果你用过流程图绘制工具，那么可能会好奇节点之间的连接线是如何计算出来的：

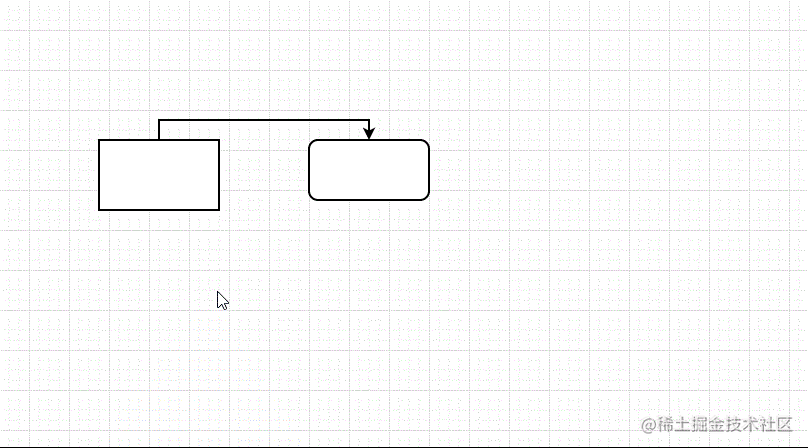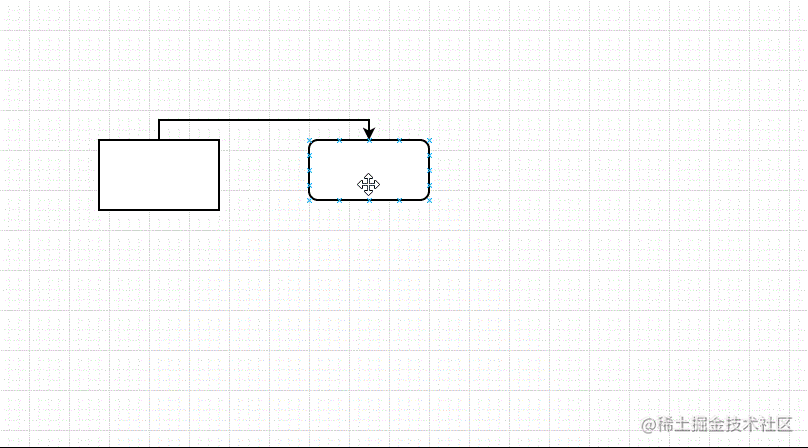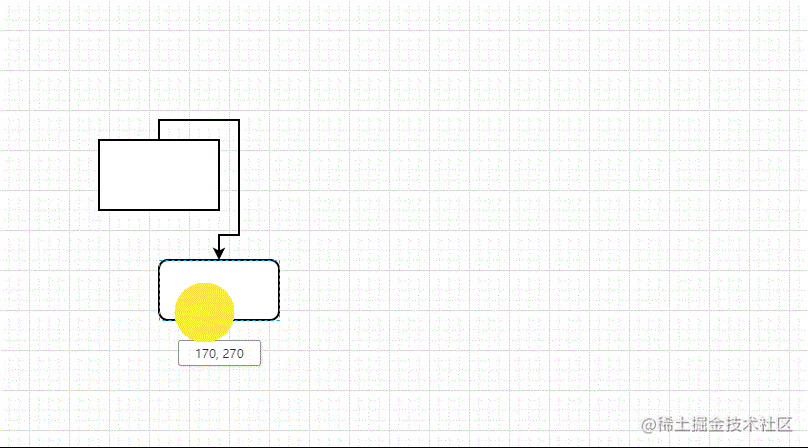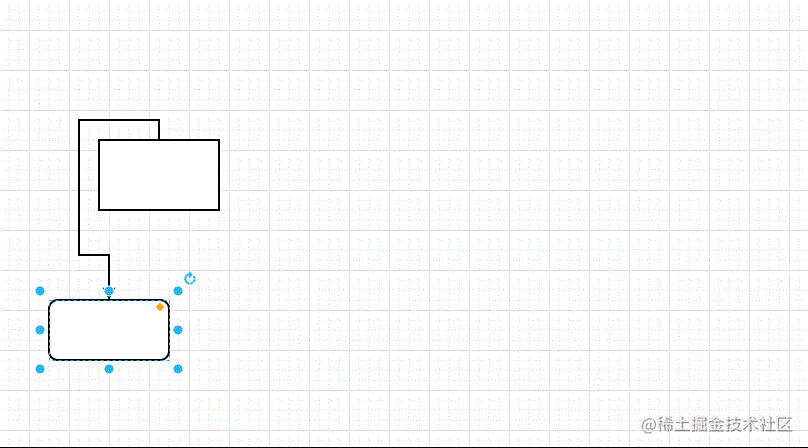
不要走开，跟随本文一起来探究一下吧。

最终效果预览：wanglin2.github.io/Association…

基本结构

先使用Vue3搭建一下页面的基本结构，为了简化canvas操作，我们使用konvajs库来绘制图形。

页面模板部分，提供一个容器即可：

<div class="container" ref="container"></div> 

js部分，主要是使用konvajs来创建两个可拖拽的矩形元素及一个连接线元素，当然目前连接线并没有顶点数据：

import { onMounted, ref } from "vue";
import Konva from "konva";

const container = ref(null);

// 创建两个矩形、一个折线元素
let layer, rect1, rect2, line;

// 矩形移动事件
const onDragMove = () => {// 获取矩形实时位置console.log(rect1.x(), rect1.y(), rect2.x(), rect2.y());
};

// 初始化图形
const init = () => {const { width, height } = container.value.getBoundingClientRect();// 创建舞台let stage = new Konva.Stage({container: container.value,width,height,});// 创建图层layer = new Konva.Layer();// 创建两个矩形rect1 = new Konva.Rect({x: 400,y: 200,width: 100,height: 100,fill: "#fbfbfb",stroke: "black",strokeWidth: 4,draggable: true,// 图形允许拖拽});rect2 = new Konva.Rect({x: 800,y: 600,width: 100,height: 100,fill: "#fbfbfb",stroke: "black",strokeWidth: 4,draggable: true,});// 监听进行拖拽事件rect1.on("dragmove", onDragMove);rect2.on("dragmove", onDragMove);// 矩形添加到图层layer.add(rect1);layer.add(rect2);// 创建折线元素line = new Konva.Line({points: [],// 当前它的顶点数据是空的，所以你还看不见这个元素stroke: "green",strokeWidth: 2,lineJoin: "round",});// 折线添加到图层layer.add(line);// 图层添加到舞台stage.add(layer);// 绘制layer.draw();
};

onMounted(() => {init();
}); 

效果如下：

接下来我们只要在图形拖拽时实时计算出关联线的顶点然后更新到折线元素里就可以绘制出这条连接线。

计算出关联线最有可能经过的点

整个画布上所有的点其实都是可能经过的点，但是我们的连接线是【横平竖直】的，且要尽可能是最短路线，所以考虑所有的点没有必要，我们可以按照一定规则缩小范围，然后再从中计算出最优路线。

首先起点和终点两个点肯定是必不可少的，以下图为例，假设我们要从左上角的矩形顶部中间位置连接到右下角的矩形顶部中间位置：

接下来我们定两个原则：

1.连接线尽量不能和图形的边重叠

2.连接线尽量不能穿过元素

为什么说尽量呢，因为当两个元素距离过近或有重叠的话这些都是无法避免的。

结合上面两个原则我们可以规定元素周围一定距离内都不允许线经过（当然除了连接起终点的线段），这样就相当于给元素外面套了个矩形的包围框：

经过起终点且垂直于起终点所在边的直线与包围框的交点一定是会经过的，并且这两个点是唯一能直接和起终点相连的点，所以我们可以把这两个点当做是“起点"和"终点”，这样在计算的时候可以少计算两个点：

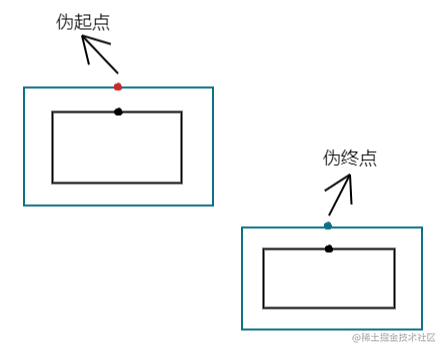
在矩形移动事件里进行点的计算，首先缓存一下矩形的位置和尺寸信息，然后定义起点和终点的坐标，最后定义一个数组用来存放所有可能经过的点：

// 矩形移动事件
const onDragMove = () => {computedProbablyPoints();
};

// 计算所有可能经过的点
let rect1X, rect1Y, rect1W, rect1H, rect2X, rect2Y, rect2W, rect2H;
let startPoint = null, endPoint = null;
const computedProbablyPoints = () => {// 保存矩形的尺寸、位置信息rect1X = rect1.x();rect1Y = rect1.y();rect1W = rect1.width();rect1H = rect1.height();rect2X = rect2.x();rect2Y = rect2.y();rect2W = rect2.width();rect2H = rect2.height();// 起终点startPoint = [rect1X + rect1W / 2, rect1Y];endPoint = [rect2X + rect2W / 2, rect2Y];// 保存所有可能经过的点let points = [];
} 

因为起终点可以在矩形的任一方向，所以我们写个方法来获取伪起点和伪终点，并将它们添加到数组里：

const computedProbablyPoints = () => {// ...// 伪起点：经过起点且垂直于起点所在边的线与包围框线的交点let fakeStartPoint = findStartNextOrEndPrePoint(rect1, startPoint);points.push(fakeStartPoint);// 伪终点：经过终点且垂直于终点所在边的线与包围框线的交点let fakeEndPoint = findStartNextOrEndPrePoint(rect2, endPoint);points.push(fakeEndPoint);
}

// 找出起点的下一个点或终点的前一个点
const MIN_DISTANCE = 30;
const findStartNextOrEndPrePoint = (rect, point) => {// 起点或终点在左边if (point[0] === rect.x()) {return [rect.x() - MIN_DISTANCE, rect.y() + rect.height() / 2];} else if (point[1] === rect.y()) {// 起点或终点在上边return [rect.x() + rect.width() / 2, rect.y() - MIN_DISTANCE];} else if (point[0] === rect.x() + rect.width()) {// 起点或终点在右边return [rect.x()