数学线性回归_从数学到代码的线性回归

数学线性回归

介绍 (Introduction)

If you have a background in statistics, perhaps even at high school level, you are probably familiar with Linear Regression (LR). Briefly, it is one of the core techniques used in statistics and machine learning (ML) to define a model that best describes a set observed data, D, generated by an unknown process. While you can find plenty of examples online that explains how to do LR along with example code, my post attempts to provide a stepwise breakdown of the mathematics behind Bayesian LR and further attempts to explain how to implement it using Python code. Please note that my understanding and explanation of this concept including notation, is entirely based on the chapter 3 from the book [1]. The references are provided at the end for you to have a look. For those who are familiar with the algorithm, this post may act as a revision of the concepts behind it. For those who are not familiar, I hope this post acts a guide as you dive through the concepts provided by other authors. It is essential to have some knowledge of linear algebra, probability theory and calculus to get enough out of this post. Okay let’s begin!

如果您有统计学背景，甚至在高中阶段，就可能对线性回归(LR)有所了解。 简而言之，这是用于统计和机器学习(ML)的核心技术之一，它可以定义一个最佳描述一个未知过程生成的一组观测数据D的模型。 尽管您可以在网上找到很多说明如何使用示例代码进行LR的示例，但我的文章尝试逐步介绍贝叶斯LR背后的数学原理，并进一步尝试说明如何使用Python代码实现它。 请注意，我对该概念(包括符号)的理解和解释完全基于本书[1]的第3章 。 最后提供了参考，供您查看。 对于那些熟悉算法的人，这篇文章可以作为其背后概念的修订。 对于那些不熟悉的人，我希望本文在您深入探讨其他作者提供的概念时能起到一定的指导作用。 必须具备一些线性代数，概率论和微积分的知识，才能充分利用这一知识。 好吧，让我们开始吧！

数学 (Math)

Say you have a set, D, of observed data, (tᵢ,xᵢ), obtained from an unknown process where xᵢ and tᵢ are inputs and outputs respectively. Bold xᵢ means it’s a vector. The relationship between an output of this unknown process, tᵢ and its input xᵢ, can be described by a function tᵢ = f(xᵢ,w). Geometrically, From a linear algebra point of view, once we have the right set of basis vectors, we can represent any vector/point in the vector space. The idea here is that our input lives in a D-Dimensional space, ℝᴰ, and our output lives in an M-dimensional space,ℝᴹ, which i like to call the output space. Our modeling problem now becomes finding a suitable value of M i.e. suitable number of basis and parameter values, w, that combines these basis. These basis are again, functions of x, which I believe is for tuning purposes!. These functions are referred to as basis functions. There are many functions that can be used as basis functions, such as polynomials, gaussians, sigmoids e.t.c. In the code section of this post we are going to use polynomials.

假设有一组，d，观测数据的，(tᵢ，Xᵢ)，从未知方法获得，其中x和ᵢtᵢ分别输入和输出。 大胆的Xᵢ意味着它是一个载体。 这个未知的过程，tᵢ的输出和它的输入xᵢ，之间的关系可以通过一个函数tᵢ= F进行说明(Xᵢ，W)。 在几何上，从线性代数的角度来看，一旦有了正确的基向量集，我们就可以表示向量空间中的任何向量/点。 这里的想法是我们的​​输入生活在D维空间ℝᴰ中，而我们的输出生活在M维空间ℝᴹ中，我喜欢将其称为输出空间。 现在，我们的建模问题是找到合适的M值，即合适的基数和参数值w ，将这些基数组合在一起。 这些基础还是x的函数，我相信这是出于调整的目的！。 这些功能称为基本功能。 有许多可用作基本函数的函数，例如多项式，高斯，S形等。在本文的代码部分中，我们将使用多项式。

Image by Author based on [1] and [2]

作者基于[1]和[2]的图像

This function describes a pattern in this data, and if there is indeed a pattern, next time we have an input xᵢ, we expect to measure the same output tᵢ, which can also be predicted by our function. However, practically this will not be entirely accurate as there is always some noise in our measurements. Therefore, our function should account for this noise. Our observations will tend to center around our function prediction. Because of the central limit theorem, the distribution of these predictions approximates to a Gaussian distribution.

此功能介绍了此数据的模式，如果有确实是一个模式，下一次我们有一个输入xᵢ，我们预计测量相同的输出tᵢ，这也可以通过我们的函数预测。 但是，实际上这并不完全准确，因为在我们的测量中总会有一些噪声。 因此，我们的功能应考虑到这种噪音。 我们的观察将倾向于围绕我们的功能预测。 由于中心极限定理 ，这些预测的分布近似于高斯分布。

Image by Author based on [1]

作者基于[1]的图片

The joint probability of all of observations, assuming that they are independent and identically distributed (i.i.d) is a product of the probability distributions of the individual observations, expressed below.

假设所有观测值都是独立且均等分布的(iid)，则其联合概率是各个观测值的概率分布的乘积，如下所示。

Image by Author based on [1]

作者基于[1]的图片

This expression is called likelihood, and if we apply log on both sides so that we can work with additions instead of products we obtain the expression below.

该表达式称为似然性 ，如果我们在两边都应用对数，以便我们可以使用加法运算而不是乘积运算，则会获得以下表达式。

Image by Author based on [1] and [2]

作者基于[1]和[2]的图像

The greek Φ symbol is called the design matrix, we will see one way of building this in the code section. t is a column vector of output observations tᵢ and X is a matrix where each row is an observation xᵢ. Assuming we fix a value for M, the values of the parameters of our model that maximizes the likelihood has a closed form solution, referred to as the Maximum likelihood estimate.

希腊的Φ符号称为设计矩阵，我们将在代码部分中看到一种构建方式。 t为输出观测的列向量tᵢ和X是一个矩阵，其中每行是一个观测Xᵢ。 假设我们为M固定一个值，则模型中使似然最大化的参数值具有封闭形式的解，称为“ 最大似然估计” 。

Image by Author

图片作者

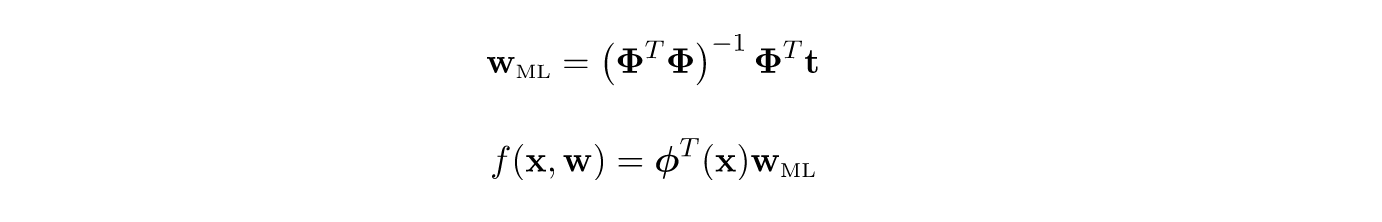
To get the intuition for maximum likelihood, let’s do a simple thought experiment. Say we flip a coin once, maybe we get a Tail. Okay, let’s flip for a second time, aand we get a Tail again. Okay, maybe this coin is flawed. Let’s flip one more time, and again this time we still get a tail. Based on these observations we might as well conclude that the chances of getting a Tail are 100%. But we know that our coin is fair i.e. prior knowledge. Using Baye’s theorem, we use this prior knowledge to come up with a better expression for computing our parameter w.

为了获得最大可能性的直觉，让我们做一个简单的思想实验。 假设我们抛硬币一次，也许我们会得到一个尾巴。 好吧，让我们再翻一下，然后我们再次得到一条尾巴。 好吧，也许这枚硬币有缺陷。 让我们再翻一次，这一次我们仍然有一条尾巴。 根据这些观察结果，我们还可以得出结论，得到一条尾巴的机会是100％。 但是我们知道我们的硬币是公平的，即先验知识。 使用贝叶斯定理，我们使用此先验知识提出了一个更好的表达式来计算参数w 。

Image by Author based on [1]

作者基于[1]的图片

Applying log to both sides of the equation and solving for the optimum parameter w , as it was done before, we obtain the expression below and the parameter estimate below it. This is called Maximum a Posteriori estimate (MAP).

如前所述，将log应用于方程式的两边并求解最佳参数w ，我们得到下面的表达式和下面的参数估计。 这称为最大后验估计 (MAP)。

Image by Author

图片作者

Both both maximum likelihood and maximum a posteriori only gives us an exact estimate of model parameters which we can later use to make predictions. However, when making predictions it’s important to have a measure of uncertainty so that we make proper decisions from the predictions. Clearly if we end here it’s not sufficient for building a robust model.

最大似然和最大后验都只给我们模型参数的精确估计，我们以后可以用它来进行预测。 但是，在进行预测时，重要的是要有一定的不确定性，以便我们根据预测做出正确的决定。 显然，如果我们在这里结束，还不足以构建健壮的模型。

The Bayesian approach (BLR), takes maximum a posteriori one step further to form a predictive distribution. From this distribution, each future input will have corresponding target mean and variance/covariance. Below is a high level view of the math.

贝叶斯方法(BLR)将后验最大化，进一步形成了预测分布。 根据此分布，每个将来的输入将具有相应的目标均值和方差/协方差。 下面是数学的高级视图。

Image by Author

图片作者

Now the predictive distribution can be obtained using the equation below

现在可以使用以下公式获得预测分布

Image by Author

图片作者

Both the posterior parameter distribution and predictive distribution can be obtained using the conditional and marginal distribution properties of gaussian distribution. See chapter 2 of [1] for more details.

可以使用高斯分布的条件和边际分布属性来获得后验参数分布和预测分布。 有关更多详细信息，请参见[1]的第2章。

In all of the methods above, we have assumed that the variance of our data and parameters (i.e w), β⁻¹ and α⁻¹, respectively are known. In practice these values are unknown and can be estimated from the dataset. A full Bayesian treatment, which i’m not going to cover in this post, offers a technique called evidence approximation that can be used to approximate these values. However, there are a couple of things worth pointing out and I will just mention them here. If α⁻¹ is very high, w will approximate to the maximum likelihood estimate. If the dataset is very small, w will approximate to the prior. As the dataset size increases towards infinity, the variance of our predictions become smaller approaching the limit β⁻¹.

在上述所有方法中，我们假设数据和参数(即w )， β-1和α-1的方差是已知的。 实际上，这些值是未知的，可以从数据集中进行估计。 完整的贝叶斯处理(我将在本文中不涉及)提供了一种称为证据近似的技术，可用于近似这些值。 但是，有两点值得指出，我在这里只提及它们。 如果α-1非常高，则w将近似于最大似然估计。 如果数据集非常小，则w将近似于前一个。 随着数据集的大小朝着无穷大方向增加，我们的预测方差会变得越来越小，接近极限值β⁻¹ 。

码 (Code)

Using Python code, let’s begin by constructing the design matrix. As stated earlier, we are going to use polynomial basis functions in this case.

使用Python代码，让我们开始构建设计矩阵。 如前所述，在这种情况下，我们将使用多项式基函数。

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(100)


def Phi(X,M=3):
  """
  This function builds up the Phi matrix using polynomial basis functions
  parameters
  X   :   X input data of shape (N,1) we are using 1-D inputs in this example
  M   :   Number of model parameters. Polynomials of up to M-1 can be modeled
  return
  Phi :   Numpy array of shape (N,M)
  """
  N = X.shape[0]
  Phi = [np.ones((N,)).reshape(-1,1)]
  for degree in range(1,M):
    Phi.append(X**degree)
  Phi = np.hstack(Phi)
  return Phi

Lets first create a class for doing regression using maximum likelihood estimate (ML):

首先创建一个使用最大似然估计(ML)进行回归的类：

class RegressionML:
  """
  This class creates a prediction model using the ML estimate.
  """
  def __init__(self):
    self.w_ML = None
  def train(self, Phi,t):
    self.w_ML = np.linalg.inv(Phi.T @ Phi) @ Phi.T @ t
  def predict(self,Phi):
    return Phi @ self.w_ML

Now let’s create a class for doing prediction using Maximum a Posteriori (MAP):

现在，让我们创建一个用于使用最大后验概率(MAP)进行预测的类：

class RegressionMAP:
  """
  This class creates a prediction model using the MAP estimate.
  As stated earlier, data and parameter variance are assummed to be
  known and should be passed as standard deviations in during instantiation.
  """
  def __init__(self,sigma_data=.5, sigma_params=.5):
    self.alpha  = np.sqrt(1/sigma_params)
    self.beta   = np.sqrt(1/sigma_data)
    self.w_MAP = None
  def train(self, Phi,t):
    D= Phi.shape[1]
    self.w_MAP = np.linalg.inv(Phi.T @ Phi + (self.alpha/self.beta)*np.identity(D)) @ Phi.T @ t
  def predict(self,Phi):
    return Phi @ self.w_MAP

Finally, let’s create a class for doing Bayesian Linear Regression. Note that this is not fully Bayesian, as the α⁻¹ and β⁻¹ are assumed to be known and should be passed in as standard deviations during class instantiation.

最后，让我们创建一个用于进行贝叶斯线性回归的类。 请注意，这并不是完全的贝叶斯方法，因为假定α⁻1和β⁻1是已知的，并且应在类实例化时作为标准偏差传入。

class RegressionBLR:
  def __init__(self,sigma_data=0.5,sigma_params=.5):
    self.alpha = np.sqrt(1/sigma_params)
    self.beta = np.sqrt(1/sigma_data)
    self.Mn = None
    self.Sn = None


  def train(self,Phi,t):
    D = Phi.shape[1]
    self.Sn = np.linalg.inv(self.alpha * np.identity(D) + self.beta * Phi.T @ Phi)
    self.Mn = self.beta*self.Sn.dot(Phi.T.dot(t))
  
  def predict(self,Phi):
    pred_mean = Phi@self.Mn
    pred_std = np.sqrt(1/(self.beta) + np.diag(Phi@self.Sn@Phi.T)).reshape(-1,1)
    return pred_mean, pred_std

测试中 (Testing)

Now let’s test our models. We are going to use synthetic data, so first we create a simple function to generate synthetic data and then set some parameters and prepare training and testing data.

现在让我们测试模型。 我们将使用合成数据，因此首先我们创建一个简单的函数来生成合成数据，然后设置一些参数并准备训练和测试数据。

def f(x):
  return np.sin(2*x) + np.cos(x) + 5


#Dataset size
N = 100
#Real process data
x = np.linspace(-5,5,1000).reshape(-1,1)
y = f(x)
#Data and parameter (i.e. prior) standard deviations
sigma_data = 0.5
sigma_params = 0.5


#simulate noise in measurements
data_noise = np.random.normal(0, sigma_data, N).reshape(-1,1)


#Generate training data i.e x
X_train = np.random.uniform(-5,5,N).reshape(-1,1)
Y_train = f(X_train) + data_noise


#Preset model size.
# Note: Bayesian approach can be used to find suitable a suitable number
M = 7


#testing data (convert to Phi)
Phi_test = Phi(x,M)


#Training data i.e. (convert to Phi)
Phi_train = Phi(X_train,M)

Now create models, train, predict and plot i.e. for ML, MAP and BLR:

现在为ML，MAP和BLR创建模型，训练，预测和绘图：

#ml
model_ml = RegressionML()
model_ml.train(Phi_train,Y_train)
ml_pred = model_ml.predict(Phi_test)


#map
model_map = RegressionMAP()
model_map.train(Phi_train,Y_train)
map_pred = model_map.predict(Phi_test)


#blr
model = RegressionBLR()
model.train(Phi_train,Y_train)
pred_mean, pred_std = model.predict(Phi_test)


plt.figure(figsize=(10,10))
plt.plot(x,y,label="Real process")
plt.plot(X_train,Y_train,'.',label="Training data")
plt.plot(x,pred_mean,label="Predicted mean")
plt.plot(x,ml_pred,label="Maximum likelihood prediction")
plt.plot(x,map_pred,':',label="Maximum a posteriori prediction")
plt.fill_between(x.flatten(), (pred_mean + pred_std).flatten(), (pred_mean - pred_std).flatten(), alpha=0.2,label="68% confidence bound")
plt.xlabel("inputs 'x'")
plt.ylabel("outputs 'y'")
plt.legend()
plt.show()

And finally our graph:

最后是我们的图形：

Image by Author

图片作者

结论 (Conclusion)

In this post I have tried to cover the core mathematics behind linear regression and attempted to implement it using python code. However, as you can see, the model is not the best fit for the observed data. The primary reason being that the model is not complex enough to fit the data (i.e. underfitting). Model complexity is the number of parameters, M, of the model which for this example, I have used a random value of 7. The Bayesian approach also offers an approach that can approximate the optimal value for model complexity which I may cover in another post.

在这篇文章中，我试图介绍线性回归背后的核心数学，并尝试使用python代码实现它。 但是，如您所见，该模型并不是最适合所观察数据的模型。 主要原因是模型不够复杂，无法拟合数据(即拟合不足)。 模型复杂度是模型的参数M的数量，在这个示例中，我使用了7的随机值。贝叶斯方法还提供了一种近似模型最优值的方法，我可能会在另一篇文章中介绍。 。

翻译自: https://towardsdatascience.com/linear-regression-from-math-to-code-9659132383ec

数学线性回归