动态规划01背包问题_01背包问题-动态规划算法

前言

1. 没有什么算法是小白能够看一次就明白的，只能多看几遍，自己动手画几遍动态规划的表格，才能真正理解其中的意思。
2. 多点耐心，多看几篇相似的文章，看多了自然会有体会。

题目描述

有 N 件物品和一个容量为 V 的背包。第 i 件物品的体积是 C[i]，价值是 W[i]。求解，将哪些物品装入背包可使价值总和最大？求出最大总价值。

设定数据

背包大小V=10，有四个物品，体积分别是[2,3,5,7]，价值分别是[2,5,2,5]。

物品价值使用int[] C表示。

物品价值使用int[] W表示

问题拆解

要求背包所能放入物品的最大价值，受限于两个因素

1. 背包的大小
2. 物品的体积和价值

但是对于物品来说，只有两个情况

1. 放入背包
2. 不放入背包

情况分析（背包V=10，四个物品体积[2,3,5,7]，价值[2,5,2,5]。）

• 只考虑将第一个物品放入背包。只要背包的体积>=2，那么都可以获得价值为2的最大价值

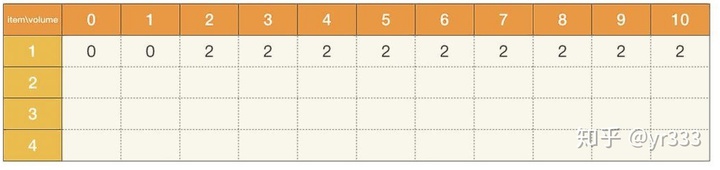
• 只考虑将前2个物品放入背包。

1. 两个物品全都放入背包。
2. 两个物品体积之和超过当前体积j的限制，只能放入其中一个价值最大的或者全都不能放入。
   1. 当i=2，j=3，只能放入其中一个价值最大且不超过容量j的物品。
   2. 当i=2，j=1，前2个物品哪个都不能放进背包。
3. 当容纳的体积j>=两个物品的体积之和，两个物品全都可以放进去。比如当j>=5。

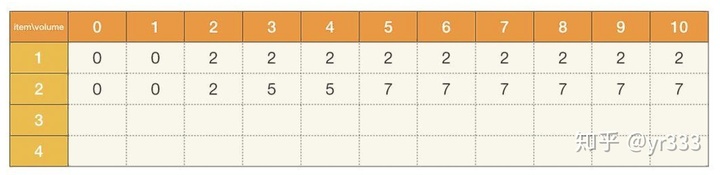
• 只考虑将前三个物品放入背包。

1. 如果容纳的体积j>=10，那么前三个物品都可以放进去，此时得到的最大价值是2+5+2=9。
2. 如果容纳的体积j小于三个物品的体积之和，那么需要考虑体积不超，价值最大的那个方案。(这里我们可以暂时使用穷举法来算一算，当考虑放前三个物品的时候，背包容纳体积j从0到10，背包所能够放入的物品的总价值。比如当j=1，不能放入物品。当j=3，只能放入一个体积为3价值为5的物品。以此类推。)

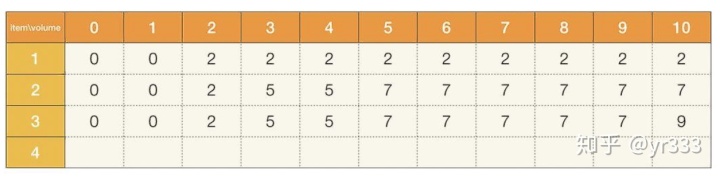
• 考虑将全部物品放进去。

1. 当我们考虑将四个物品都放入背包的时候，可以依据放入前三个物品的结果来指定方案。这样，我们就能够将这个问题拆分成了一个子问题。
2. 即 “前 n 个物品在体积 V 处的最大价值” 可以由 “前 n – 1 个物品的情况” 推导得到。
3. 状态定义：在问题拆解中，我们得知问题其实和背包的体积还有当前考虑的物品有关，因此我们可以定义dp[i][j]表示 “考虑将前 i 个物品放入体积为 j 的背包里所获得的最大价值”。
4. 递推方程：当我们考虑是否将第 i 个物品放入背包的时候，这里有两种情况
   1. 情况一：不放入，也就是不考虑第 i 个物品，那么问题就直接变成了上一个子问题，也就是考虑将 i – 1 个物品放入背包中，这样当前问题的解就是之前问题的解：dp[i][j]=dp[i-1][j]
   2. 情况二：放入：如果背包体积大于第 i 个物品的体积，我们可以考虑将第 i 个物品放入，这个时候我们要和之前的状态做一个比较，选取最大的方案：dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-C[i]]+W[i]) （这里一定要仔细去体会，算法关键）

• C[i]:第i个物品的体积
• W[i]：第i个物品的价值
• j-C[i]：体积j减去c[i]之后剩下的体积
• dp[i-1][j-C[i]]：第i-1行，体积为(j-C[i])时所能放入物品的最大价值
• 放入第i个物品之后的总价值，价值不一定比没放第i个物品的价值大

算法实现

• 实现这一环节还是主要考虑状态数组如何初始化，每次都要考虑 i – 1，另外还要考虑背包体积为 0 的情况，因此初始化数组时多开一格可以省去不必要的麻烦。
• 也就是，第0行和第0列不计入。

 /**
     * dp[i][j]：体积为j时，在选择前i个物品放入背包中，所能放入背包内的最大价值。
     *           前i个物品中不一定全部放入，i之后的物品不能放入。
     *
     * @param V 背包最大容纳体积
     * @param C C[i-1] 第i个物品的体积
     * @param W W[i-1] 第i个物品的价值
     * @return
     */
    public int bag(int V, int[] C, int[] W) {
        if(V<=0||C.length!=W.length){
            return 0;
        }
        int n = C.length;
        int[][] dp = new int[n + 1][V + 1];
        //第i行j列，没有算0行0列
        for (int i = 1; i <= n; i++) {
            for (int j = 1; j <= V; j++) {
                dp[i][j] = dp[i - 1][j];
                if (j > C[i - 1] && dp[i - 1][j] < dp[i - 1][j - C[i - 1]] + W[i - 1]) {
                    dp[i][j] = dp[i - 1][j - C[i - 1]] + W[i - 1];
                }
            }
        }
        return dp[n][V];
    }

我们根据算法走一遍整个流程

• int[][] dp =newint[n +1][V+1]; dp数组的元素初始值全部设置为0。
• 判断条件 if(V>C[i -1]&& dp[i -1][j]< dp[i -1][j -C[i -1]]+W[i -1])
  • 如果背包体积j大于当前第i个物品的体积，并且在放入第i个物品之后所能获得的价值大于没有放入第i个物品的价值，那么就放入第i个物品。
• i=1，j=1，dp[1][1]=dp[0][1]=0;判断条件不满足
• i=1，j=2，dp[1][2]=dp[0][2]，判断条件成立，求得dp[1][2]=dp[0][1-0]+2=2;
• i=1，j>=2，都可以求得dp[1][j]=2;
• i=2，j=1，dp[2][1]=dp[1][1]=0，判断条件不满足
• i=2，j=2，dp[2][2]=dp[1][2]=2,，判断条件不满足
• i=2，j=3，dp[2][3]=dp[1][3]=2,，判断条件满足，dp[2][3]=dp[1][3-0]+5=dp[1][0]+5=5;
• 以此类推

心得

1. 动态规划核心思想：记住你之前求解的答案。