rsa加密 过程 离散数学_rsa和离散日志进一步崩溃

rsa加密 过程 离散数学

A while back a number of RSA challenges were created, such as for RSA-240 (and which has 240 decimal digits — 795 bits) [here]:

不久之前，创建了许多RSA挑战，例如RSA-240(具有240个十进制数字-795位)[ 在这里 ]：

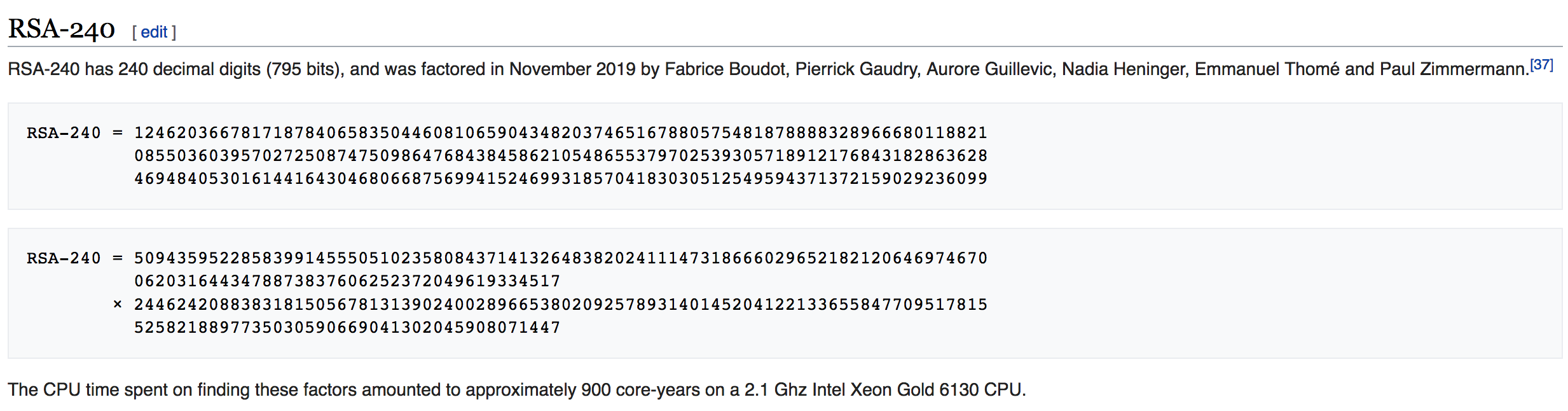
But this week it was broken with:

但是这周它被打破了：

RSA-240 = 12462036678171878406583504460810659043482037465167880575481878888328 966680118821085503603957027250874750986476843845862105486553797025393057189121 768431828636284694840530161441643046806687569941524699318570418303051254959437 1372159029236099 = 509435952285839914555051023580843714132648382024111473186660296521821206469746 700620316443478873837606252372049619334517 times 244624208838318150567813139024002896653802092578931401452041221336558477095178 155258218897735030590669041302045908071447

This means that anything encrypted with anything less than 1,024 bits in RSA is in danger of being cracked. The new crack advances the state-of-the-art from 768 bits (cracked in December 2009) to 795 bits. The great advancement with his crack is that the researchers also broken a 795-bit discrete log problem, too. This is the first time that both the integer factorization of RSA and the discrete log problem (DLP) has been cracked together, and using the same hardware and software (CADO-NFS software with the Number Field Sieve algorithm). This cracking equates to 4,000 core-years and used Intel Xeon Gold 6130 CPUs:

这意味着用RSA中少于1,024位加密的任何数据都有被破解的危险。 新的破解将最先进的技术从768位(2009年12月破解)提高到795位。 他的破解取得的巨大进步是，研究人员还解决了795位离散对数问题。 这是首次使用相同的硬件和软件(具有Number Field Sieve算法的 CADO-NFS软件 )将RSA的整数分解和离散对数问题(DLP)一起破解。 这种破解相当于4000核年，并使用了英特尔至强金牌6130 CPU：

The results are:

结果是：

• RSA-240 sieving: 800 physical core-years.
  RSA-240筛选：800个物理核心年。
• RSA-240 matrix: 100 physical core-years.
  RSA-240矩阵：100个物理核心年。
• DLP-240 sieving: 2400 physical core-years
  DLP-240筛分：2400物理核年
• DLP-240 matrix: 700 physical core-years
  DLP-240矩阵：700个物理核心年

破解RSA？ (Cracking RSA?)

So if you have factored the modulus, how do you crack the cipher? With this we are using the RSA encryption method, and we have the encryption key (e,N). We must find the two prime numbers which create the value of N (p and q), and must use a factorization program to find them. Once we find the factors it is easy to then determine the decryption key (d,N).

因此，如果您已经考虑了模数，那么如何破解密码？ 这样，我们正在使用RSA加密方法，并且我们有了加密密钥(e，N)。 我们必须找到两个创建N值的质数(p和q)，并且必须使用分解程序来找到它们。 一旦找到因素，就可以轻松确定解密密钥(d，N)。

Here is an example:

这是一个例子：

Encryption parameters
e:	65537
N:	1034776851837418228051242693253376923
Cipher:	582984697800119976959378162843817868
We are using  60 bit primes

Now we have to crack N by finding the primes that make up the value.

现在，我们必须通过找到构成值的素数来破解N。

If we use this [link], we get:

如果使用此[ 链接 ]，则会得到：

Factors
-------
1,034,776,851,837,418,228,051,242,693,253,376,923 = 1,086,027,579,223,696,553 x 952,809,000,096,560,291

p=1,086,027,579,223,696,553 q=952,809,000,096,560,291

p = 1,086,027,579,223,696,553 q = 952,809,000,096,560,291

Now we work out PHI, which is equal to (p−1)×(q−1):

现在我们计算出PHI，它等于( p -1)×( q -1)：

>>>p=1086027579223696553
>>>q=952809000096560291
>>> print (p-1)*(q-1)
1034776851837418226012406113933120080

Now we find e⁻¹ (mod PHI) (and where (d×e) (mod PHI)=1), such as using [here]:

现在我们找到e⁻¹ ( PHI模) (以及其中( d × e )( PHI模) = 1)，例如使用[ here ]：

Inverse of  65537  mod  1034776851837418226012406113933120080
Result: 568411228254986589811047501435713

This is the decryption key. Finally we decrypt with Message=Cipherᵈ (mod N):

这是解密密钥。 最后，我们使用Message = Cipherᵈ( mod N)解密：

>>> d=568411228254986589811047501435713
>>> cipher=582984697800119976959378162843817868
>>> N=1034776851837418228051242693253376923
>>> print pow(cipher,d,N)
345

The message is 345

消息是345

Finally, let’s check the answer. So we can re-cipher with the encryption key and we use Cipher=Mᵉ (mod N):

最后，让我们检查一下答案。 因此，我们可以使用加密密钥重新加密，然后使用Cipher = Mᵉ (mod N) ：

>>> m=345
>>> e=65537
>>> N=1034776851837418228051242693253376923
>>> print pow(m,e,N)
582984697800119976959378162843817868

This is the same as the cipher, so the encryption and decryption keys have worked. Thus the encryption key is [65537, 1034776851837418228051242693253376923] and the decryption key is [568411228254986589811047501435713, 1034776851837418228051242693253376923]

这与密码相同，因此加密和解密密钥已经起作用。 因此，加密密钥为[65537，1034776851837418218228051242693253376923]，解密密钥为[568411228254986589589047047501435713，1034776851837418228051242693253376923]

破解2K密钥？ (Cracking 2K keys?)

In order to understand the concept of work in cracking cryptography, Lenstra [here] defined the concept of Global Security in order to show the amount of energy required to crack cryptographic algorithms and compared this with the amount of water that energy could boil something. This could be seen as the carbon footprint of cracking. For a 35-bit key symmetric key (such as AES), you only need to pay for the boiling of a teaspoon of energy, and for a 50-bit key, you just need to have enough money to pay for a shower:

为了理解破解密码学的工作概念，Lenstra [ 此处 ]定义了“全局安全性”概念，以显示破解密码算法所需的能量并将其与可能使某物沸腾的水量进行比较。 这可以看作是开裂的碳足迹。 对于35位密钥对称密钥(例如AES)，您只需要支付一茶匙能量的沸腾，而对于50位密钥，您只需要有足够的钱来支付淋浴：

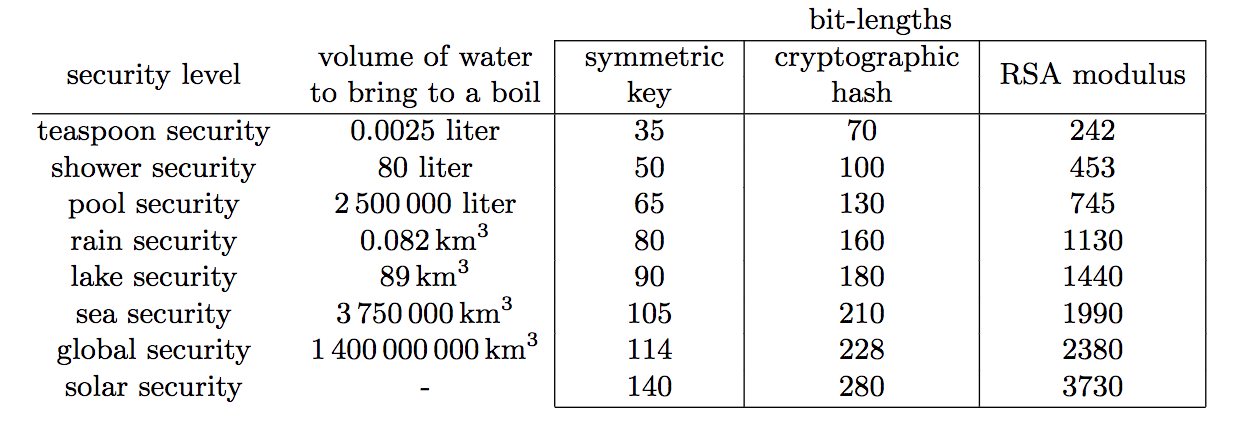
So let’s look at RSA. In order to crack it, we need to factor N, into p and q (the two prime numbers used). Once cracked we can determine PHI (p-1 x q-1), and then we can determine the decryption value (d) [here]. First we will take teaspoon security, and where we would need to consume the amount of energy that can boil a teaspoon. A sample would be (242-bit RSA modulus) [here]:

因此，让我们看一下RSA。 为了破解它，我们需要将N分解为p和q(使用的两个质数)。 一旦破解，我们可以确定PHI(p-1 x q-1)，然后可以确定解密值(d)[ 此处 ]。 首先，我们将采取茶匙安全措施，并在这里需要消耗可能煮沸一茶匙的能量。 一个样本将是(242位RSA模数)[ 此处 ]：

N=p*q= 5896261486983538627098661478596873684661596787145726508859641645687965941

The prime numbers have 121 bits, and, if we were to crack it, the prime numbers are:

质数有121位，如果要破解，则质数为：

(p): 2526944374765758521282783272842906989(q): 2333356264531983395509730755656883369

(p)：2526944374765758521282783272842906989(q)：2333356264531983395509730755656883369

Now we try pool security, which will have a 745-bit modulus [here]:

现在我们尝试池安全性，它将具有745位模数[ 这里 ]：

N=p*q= 32820593417068637302218774761235133563284012029917056683084157063791880518253729060356882948911691226183490705953686023149594165668325095998315760949745673726122108730625118573143944403355956100353972339795087626332085413773

You would then have to consume the amount of energy to boil a swimming pool of water, in order to recover p and q, and which would be:

然后，您将不得不消耗大量能量来沸腾一个游泳池 ，以恢复p和q，这将是：

(p): 5136574890107321107930054184342872847511932740355863615831749987190796683508207354267329960601590388187075433061 (q): 6389587248163902409204449208538775019640799414724150251382810569000364623759594714615114512184726059299258653193

(p)：5136574890107321107930054184342872847511932740355863615831749987190796683508207354267329960601590388187075433061(q)：6389587248163902402409204449208538775019640799414724150251382810569000364623759594714694714615114512184184059059299258653193

Now, for a 2K modulus, we would have to get the energy to boil all the seas in the world in order to factorize this [here]:

现在，对于2K模数，我们必须获得将世界上所有海洋煮沸的能量，以便将其分解为[ 此处 ]：

N=p*q= 43167595701317556262423026656965675311752941263790242843723869722559144737611460632568632166086252510023021805945735591772225470974213720757550705733352824448503063524999506226660596906575816882736759369162417329042308450768818539569647978275834799861395280256322795630706924323442073941650079693323544638961692274755658766444829616155400362106306476222028695948219411648554898625217423276610753800859051583718732195244823763757178756946886496848799638990325775625765337088319529344897632569507945680260646306289624365294219736449252864209416787913390862597496737460530614841627093463597005887159713

If you could afford the energy to boil all the seas on the planet, you would be able to recover the prime number factors of:

如果您有能力负担沸腾地球上所有海洋的能量，则可以恢复以下的质数因子：

(p): 196609148217569855881469103057436778288884865730728431036496969106242709174542556226244974424242605165013577403243273721574500460326174617160923703395095978667090714867455310166651932606597318485468745721964757615177804666962624050069365974032392172635080905056653578728556376998092239415714121906067(q): 219560463450804526512484156665207894511493329487508026519690092833541901773486924130405885017845670513121751269792879364231218578683707161192474640518621978728363979172391042793592947789410287416485864619629721775927035570271970144478351754084252110756000450203907965120369883036301470716442779209339

(P)：196609148217569855881469103057436778288884865730728431036496969106242709174542556226244974424242605165013577403243273721574500460326174617160923703395095978667090714867455310166651932606597318485468745721964757615177804666962624050069365974032392172635080905056653578728556376998092239415714121906067(Q)：219560463450804526512484156665207894511493329487508026519690092833541901773486924130405885017845670513121751269792879364231218578683707161192474640518621978728363979172391042793592947789410287416485864619629721775927035570271970144478351754084252110756000450203907965120369883036301470716442779209339

Finally we move to solar security (4K modulus) [here]:

最后，我们转向太阳能安全(4K模数)[ 此处 ]：

N=p*q= 3960081571383420167814679941098524090937928309488590816012966209196161594447717629829982817426147699500858353736336886688538212500739476494518433176312774088968991333976947698248519629991492642529120005788698131019622899051239531916630515702854026672543263467130654985378038454931630236636653155999253153667000741616739898252666802505968932136484029166497432922043251656271894573751299513374223876341473788971768959659494093660332016468558662263427959769631314190762350433414241237989194424754061077772372503406770663167105510157438848063647609081050040392193568744736442564106876056012592222564834186803873526496760807948668990042316968129375782077793420316049776474546085038021971914974545368413754514832542993932007256348508892381012868762395242004260990250419466271752664052646884549601175933263521857652478403283808673329360714989274196579539004889158891187902257130712437178153193341806763422097034483621244566078923257429637598615691552350410659591140346748167709449018947885391433407732878878772283602778821869413553383175098670195132506173740601661352893351053048344129586887687118260226198269183634491741066922963

You will never find the prime numbers, but they are:

您将永远找不到素数，但它们是：

(p): 2387628035654914041578676682340635535950948791037039903330270590495501744849764207480076462162294270197243407459110192208709737698247332428053357258855955290692393471421516310661792749482905080962109692416944336517049095407867686284521225687878370847230533829287501911033500368831913293493330562838467387835530549969054109399131451846959457130413492668037089837378118350872377084885693225874836148717207853352068189405415387476462556003921350678166912349980061364631958090280213640154021116006326720158290040518790513066623093136091263566334119222952846436577451(q): 1658583963769377603578396329705793644732710623310129654038348230711585763044092787355651332948374169988931521882298144371384733551640579147022118494636732293264604461116977329421823894181755805820089237394172033870263627093736577790369697957516336302977958796425947479274422794199973433467842572527064416348509712003954901454840352976743534063167992440103943082723957859216188269111695713462656653049479588103312185114742167076660911677070759504987871743971457634287384430572107927280368523691106585718147625665698291217102305172813935222056309427697965967221113

(p)：( q)：

结论 (Conclusions)

And so RSA and discrete logs crumble a bit more!

因此，RSA和离散日志的崩溃更多！

Your adversary has a budget for cracking, and if they have to spend the amount of energy to boil the water in a teaspoon, it may be worth it. To crack 2K RSA — without a quantum computer — would require the energy to boil all the oceans on the planet — for a single key crack. No one has that energy, and no one can pay the bills for that consumption.

您的对手有一个开裂的预算，并且如果他们不得不花费大量的能量来煮沸一茶匙的水，那也许是值得的。 要破解2K RSA(而没有量子计算机)，则需要能量来煮沸地球上的所有海洋，才能实现一次关键的破解。 没有人拥有这种能量，也没有人可以为此消费付账。

If you are interested, here’s the amazing history of RSA:

如果您有兴趣，这是RSA的惊人历史：

翻译自: https://medium.com/asecuritysite-when-bob-met-alice/rsa-and-discrete-logs-crumble-a-bit-more-eecc5423b8e

rsa加密 过程 离散数学